文章目录
- 一、213. 打家劫舍 II
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 二、740. 删除并获得点数
- 1.题目简介
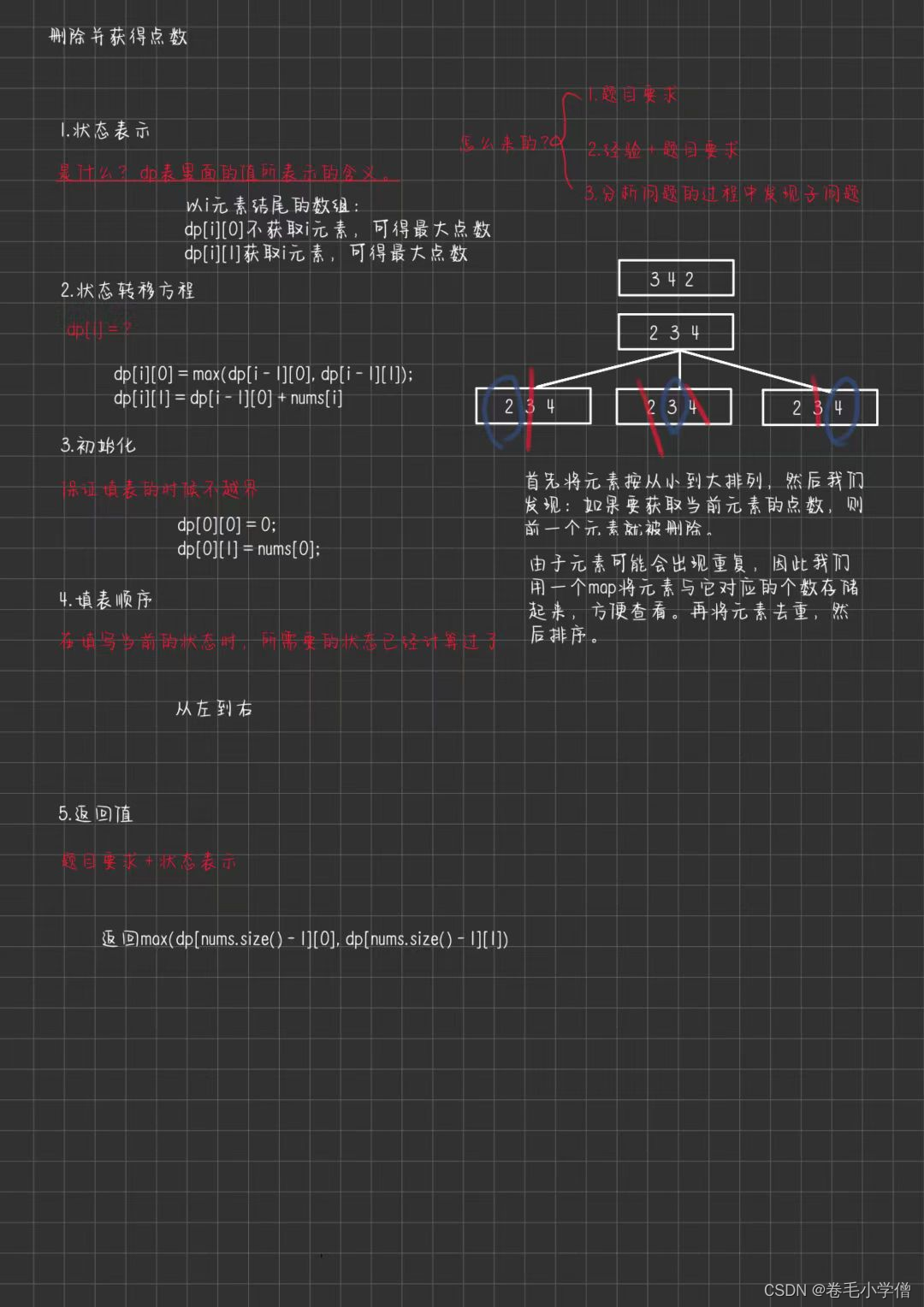
- 2.解题思路
- 3.代码
- 4.运行结果
- 三、剑指 Offer II 091. 粉刷房子
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 总结
一、213. 打家劫舍 II
1.题目简介
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。


2.解题思路

3.代码
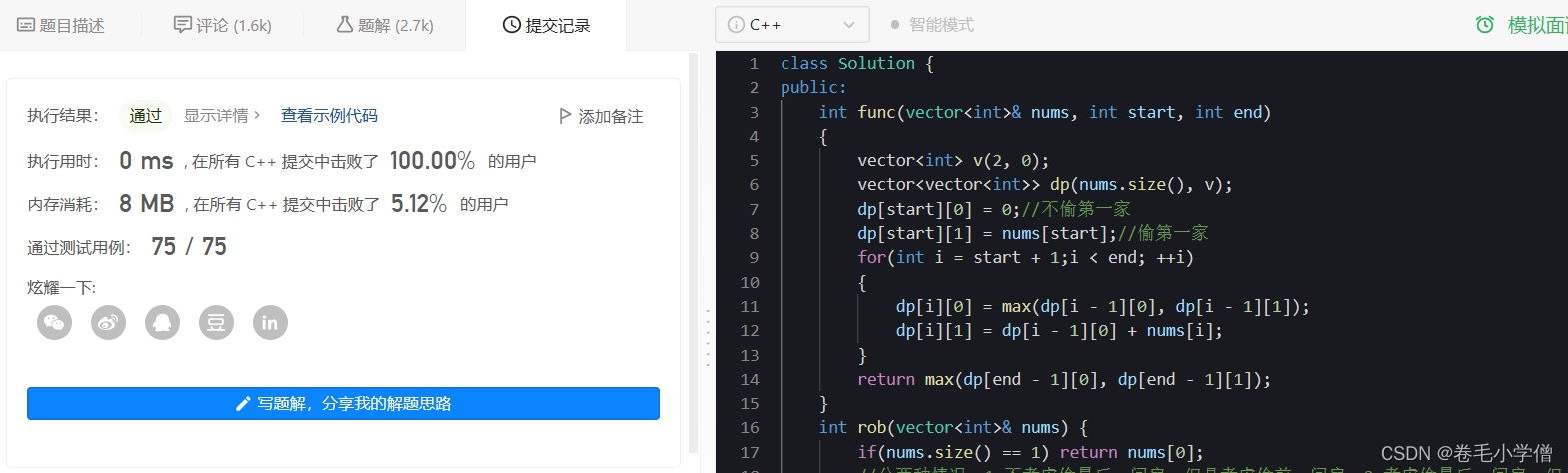
class Solution {
public:
int func(vector<int>& nums, int start, int end)
{
vector<int> v(2, 0);
vector<vector<int>> dp(nums.size(), v);
dp[start][0] = 0;//不偷第一家
dp[start][1] = nums[start];//偷第一家
for(int i = start + 1;i < end; ++i)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = dp[i - 1][0] + nums[i];
}
return max(dp[end - 1][0], dp[end - 1][1]);
}
int rob(vector<int>& nums) {
if(nums.size() == 1) return nums[0];
//分两种情况:1.不考虑偷最后一间房,但是考虑偷前一间房;2.考虑偷最后一间房,但是不考虑偷前一间房(两间房都不考虑偷的情况,隐藏在这两种情况中)
return max(func(nums, 0, nums.size() - 1), func(nums, 1, nums.size()));
}
};
4.运行结果
二、740. 删除并获得点数
1.题目简介
740. 删除并获得点数
给你一个整数数组nums,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

2.解题思路
3.代码
class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
map<int, int> m;
vector<int> v;
for(auto& e : nums)
{
m[e]++;
}
for(auto& e : m)
{
v.push_back(e.first);
}
vector<int> vp(2, 0);
vector<vector<int>> dp(v.size(), vp);
//从0~i,不删除i点可以获得的最大点数;删除i点将获得的最大点数
dp[0][0] = 0;//不删除该点可以获得的最大点数
dp[0][1] = v[0] * m[v[0]];//删除该点将获得的最大点数
for(int i = 1;i < v.size(); ++i)
{
if(v[i - 1] == v[i] - 1)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = dp[i - 1][0] + v[i] * m[v[i]];
}
else//如果前一个值与当前值并不是相邻数,则删除当前数不会影响前一个数,因此要取删除或者不删除前一个值所能得到的较大点数
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = max(dp[i - 1][0], dp[i - 1][1]) + v[i] * m[v[i]];
}
}
return max(dp[v.size() - 1][0], dp[v.size() - 1][1]);
}
};
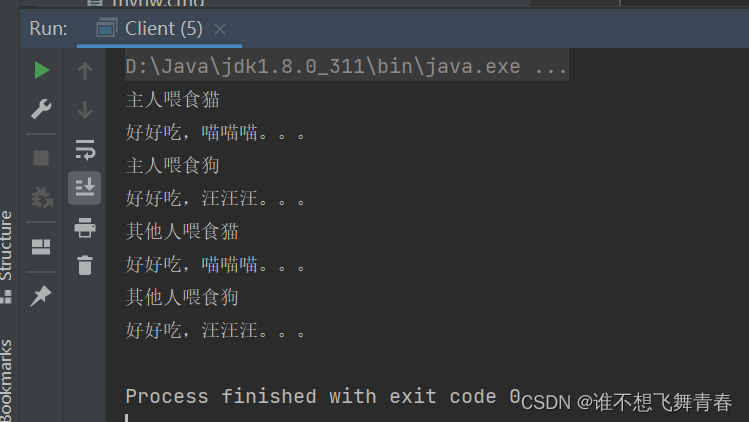
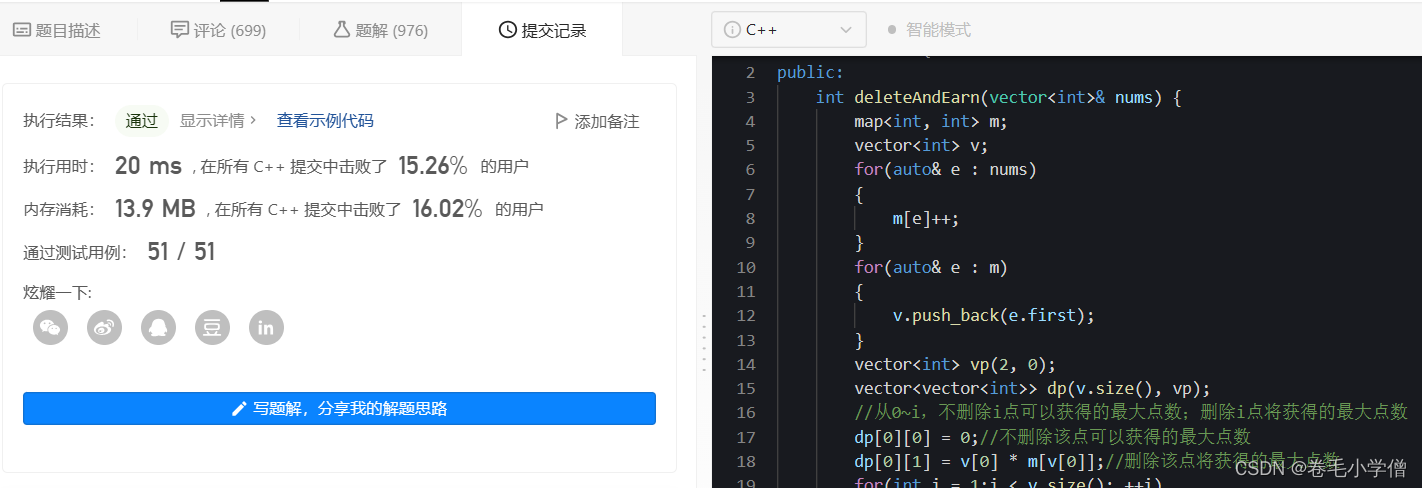
4.运行结果
三、剑指 Offer II 091. 粉刷房子
1.题目简介
剑指 Offer II 091. 粉刷房子

2.解题思路

3.代码
class Solution {
public:
int minCost(vector<vector<int>>& costs) {
vector<int> v(3, 0);
vector<vector<int>> dp(costs.size(), v);
dp[0][0] = costs[0][0];//刷红色的最小花费
dp[0][1] = costs[0][1];//刷蓝色的最小花费
dp[0][2] = costs[0][2];//刷绿色的最小花费
for(int i = 1;i < costs.size(); ++i)
{
dp[i][0] = min(dp[i - 1][1] , dp[i - 1][2]) + costs[i][0];//刷红色的最小花费
dp[i][1] = min(dp[i - 1][0] , dp[i - 1][2]) + costs[i][1];//刷蓝色的最小花费
dp[i][2] = min(dp[i - 1][0] , dp[i - 1][1]) + costs[i][2];//刷绿色的最小花费
}
return min(min(dp[costs.size() - 1][0], dp[costs.size() - 1][1]), dp[costs.size() - 1][2]);
}
};
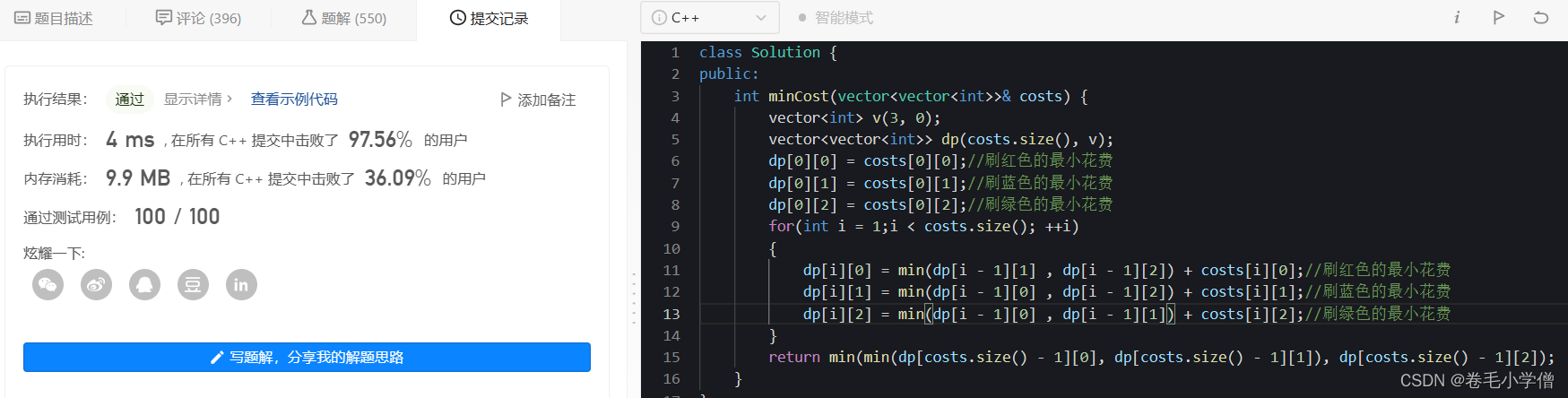
4.运行结果
总结
今天是算法练习的第4天。
宝剑锋从磨砺出,梅花香自苦寒来,继续加油!
如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!