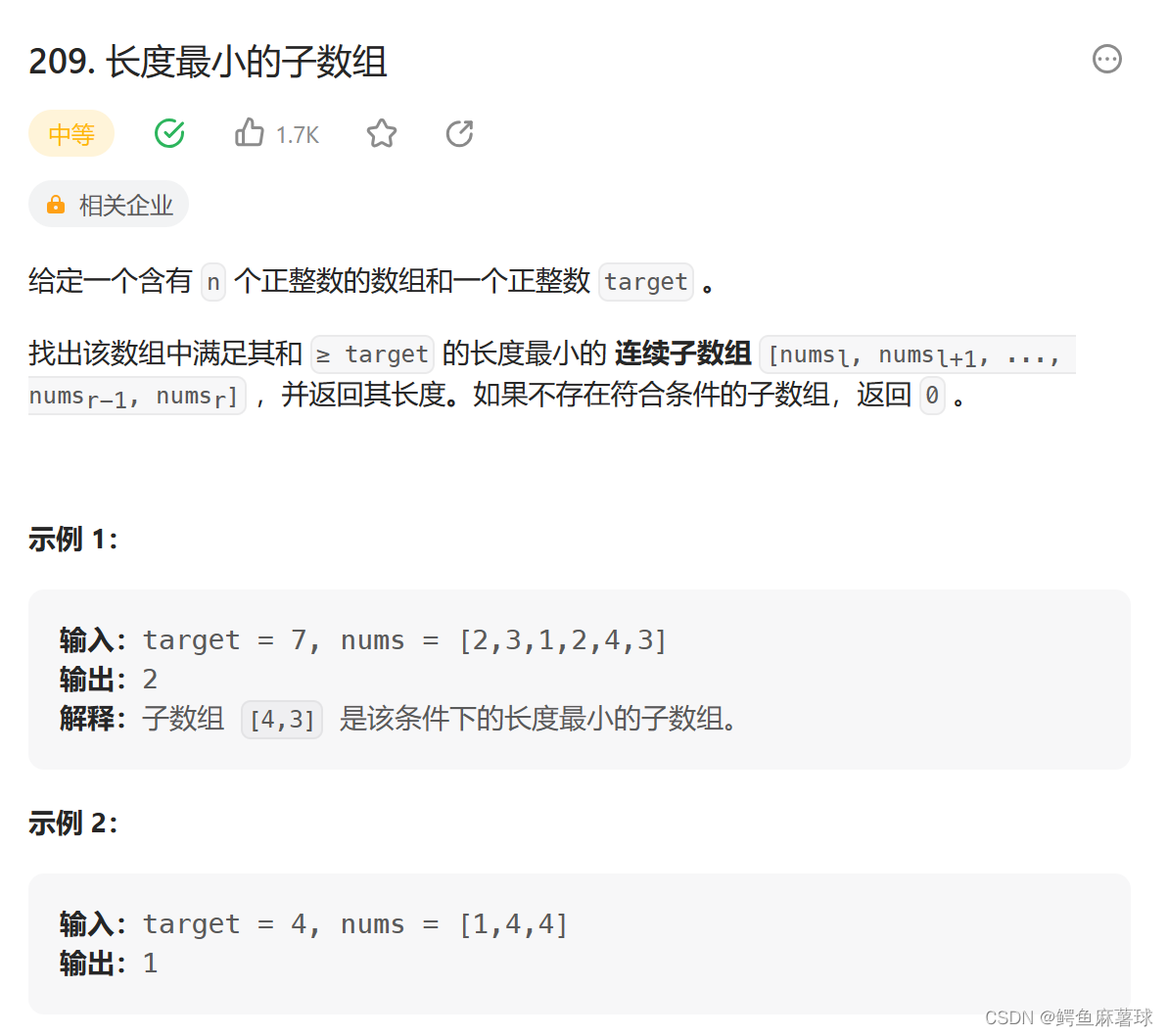
209.长度最小的子数组
解法思想来自代码随想录:209.长度最小的子数组
(1)暴力解法
我们暴力解法直接使用两个for循环,然后不断的遍历寻找符合条件的子序列;
初始化长度变量length和结果变量result为0和int类型最大数。初始化变量sum为0,表示当前子数组的和。
第一层循环从0到numsSize-1枚举子数组的起始位置i。第二层循环从i开始到numsSize-1枚举子数组的结束位置j。 在每次循环中将nums[j]加入sum中,表示当前子数组的和。这样子我们通过两重循环,就可以枚举出所有的情况,接下来只要找到符合条件的最小子序列就可以了。
所有当sum>=target,说明当前子数组的和已经大于等于目标值,是我们满足条件的一个答案,但是不一定是最小的一个。我们求出当前子数组的长度length为j-i+1,并不断的更新result为length和原先result中的较小值。
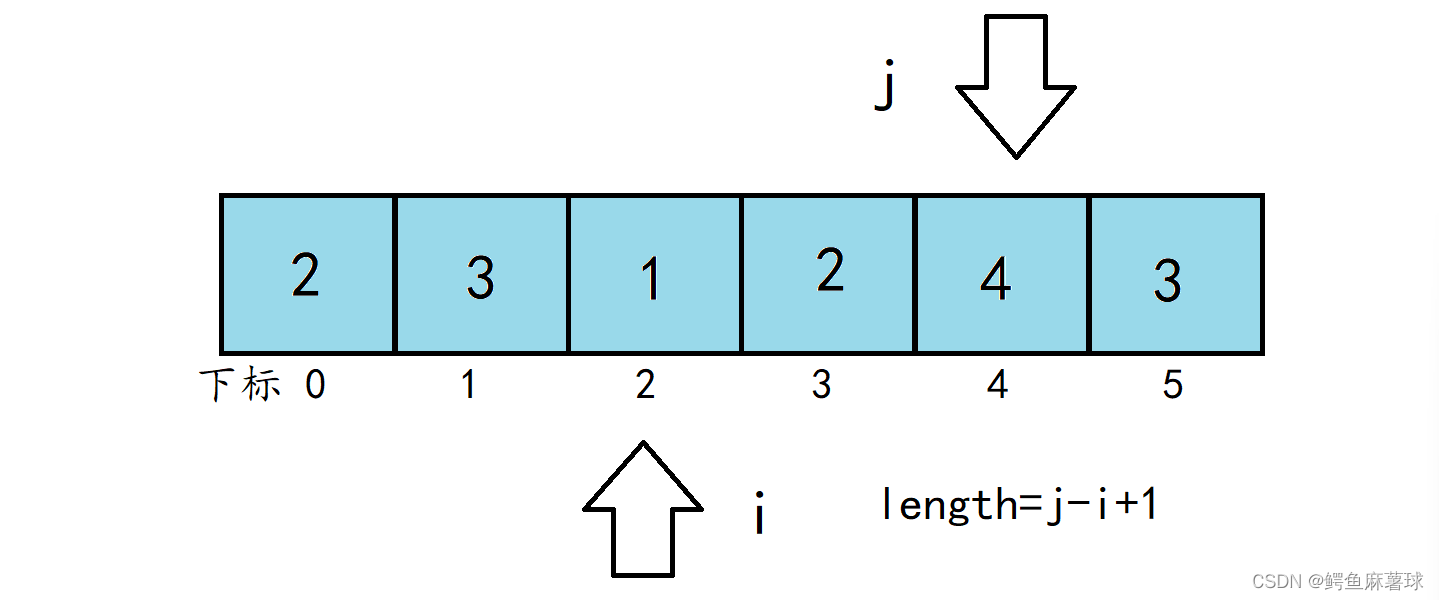
最后返回result。特别地,如果result仍然为int类型最大数,则数组中不存在符合条件的子数组,返回0表示无解。
int minSubArrayLen(int target, int* nums, int numsSize){
int length=0;
int result=INT32_MAX;
int i=0,j=0;
int sum=0;
for(i=0;i<numsSize;i++)
{
sum=0;
for(j=i;j<numsSize;j++)
{
sum+=nums[j];
if(sum>=target)
{
length=(j-i+1);
result=length<result?length:result;
}
}
}
return result==INT32_MAX?0:result;
}
由于时间复杂度较高,leetcode只能通过18/20的用例。
时间复杂度:O(n^2)
空间复杂度:O(1)
(2)滑动窗口
代码随想录详解
滑动窗口类型于双指针法,我们可以不断的调节子序列的起始位置和终止位置,从而得出长短最小的子数列长度。
初始化变量sum为0,表示当前子数组的和。初始化变量result为int类型的最大值,表示暂时解为0。初始化变量length为0,表示当前子数组长度。初始化双指针i和j为0,i表示当前子数组的右边界,j表示当前子数组的左边界。
第一层循环从0到numsSize-1枚举子数组的右端点i。在每次循环中将nums[i]加入sum中,表示当前子数组的和。
使用while循环,如果sum>=target,则说明当前子数组的和已经大于等于目标值。我们先将所满足要求的一个答案储存以便之后不断比较,此时需要开始缩短左边界,寻找更短的子数组。循环条件为sum>=target。
将当前子数组的长度length设为i-j+1,并更新result为length和原先result中的较小值。将nums[j]从sum中减去,表示缩小左边界。将左指针j指向下一个元素。
循环结束后返回result。如果result仍然为无穷大,则数组中不存在符合条件的子数组,返回0。
int minSubArrayLen(int target, int* nums, int numsSize){
int sum=0;
int result=INT32_MAX;
int length=0;
int i=0,j=0;
for(i=0;i<numsSize;i++)
{
sum+=nums[i];
while(sum>=target)
{
length=i-j+1;
sum-=nums[j];
j++;
result=result>length?length:result;
}
}
return result==INT32_MAX?0:result;
}
滑动窗口可以根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。 每个元素在滑动窗口的进入和出去各操作一次,每个元素被操作两次,时间复杂度为2*n为O(n);
时间复杂度:O(n)
空间复杂度:O(1)