计算机视觉中，有哪些基于控制点对的图像变换？

news2025/1/10 12:11:28

这里探讨的所有图像变换（二维）都是基于控制点对的，它们的主要区别在于：
1、它们是如何通过两张图像的控制点对产生变换场（变换矩阵或者变换公式中的参数）的
2、控制点之间的对应关系严格程度

这里说的变换是如何做到的？

得到变换场后，对原图像的所有坐标应用变换公式得到变换后的坐标，再根据变换后的坐标（可能非整数）利用某种插值方法从原图像中采样像素值，即可得到变换后的图像。

这里我们涉及到正反过程：已知变换场求变换后的图像，和已知变换前后的图像并选择若干控制点对求变换矩阵。

1、仿射变换（Affine Transformation）

仿射变换是简单的线性变换，当你需要一个简单的几何变换如放缩、旋转和平移时可以用到。（刚性变换、相似变换等更简单的变换这里不再讲述。）

给定一个坐标(x,y)，所要得到变换后的坐标(u, v)，仿射变换使用一个3x3的变形矩阵（下式是齐次方程的形式，实际上有意义的矩阵参数只有a,b,c,d,e,f六个）实现：

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} a& b& e\\ c& d& f\\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

这里的a,b,c,d用于控制旋转、缩放变化，而e、f用于控制平移变换。

反之，若已有坐标点对（控制点点对），要求得仿射变换矩阵，只需要对上式求解，6个未知数共需要6个方程，即3对不共线的点对即可。若给定的点对多于3对，则变成最小二乘问题，可以同时求出一个最优的变换矩阵。

2、透视变换（Perspective Transformation）

透视变换是将图片投影到一个新的视平面。可以认为仿射变换是透视变换的一个特例。

给定一个坐标(x,y)，所要得到变换后的坐标(u,v)，透视变换使用一个3x3的变形矩阵（下式是齐次方程的形式，实际上有意义的矩阵参数只有a,b,c,d,e,f,g,h八个）实现：

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} a& b& e\\ c& d& f\\ g& h& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

这里的a,b,c,d用于控制旋转、缩放变化，e、f用于控制平移变换，g、h实现映射关系。

反之，若已有坐标点对（控制点点对），要求得透视变换矩阵，只需要对上式求解，8个未知数共需要8个方程，即4对不共线的点对即可。若给定的点对多于4对，则变成最小二乘问题，可以同时求出一个最优的变换矩阵。

3、二次变换（Quadratic Transformation）

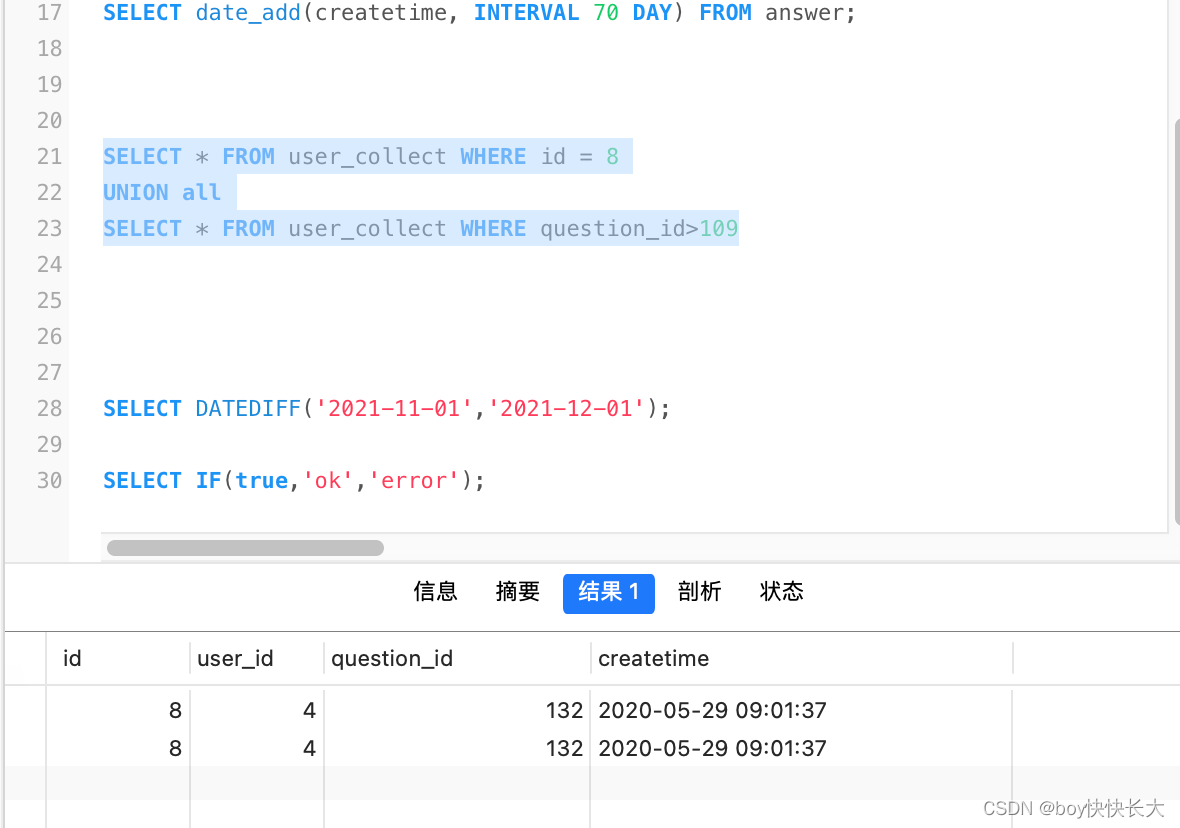
二次变换指通过二次多项式来实现图像变换。与仿射变换相比，二次变换可以表达更复杂的非线性变换关系。

二次变换可以实现：

简单的仿射变换效果（当高次项系数为空时）
带有微幅扭曲变形
非线性变形，但受二次多项式限制，曲线变化有限

给定一个坐标(x,y)，所要得到变换后的坐标(u,v)，二次变换使用如下规则：

$u=a_0+a_1x+a_2y+a_3x^2+a_4y^2+a_5xy$

$v=b_0+b_1x+b_2y+b_3x^2+b_4y^2+b_5xy$

这里的 $a_*,b_*$ 为多项式系数，一共12个，用于控制变形程度。

反之，若已有坐标点对（控制点点对），要求得二次变换的参数，只需要对上式求解（可以采用SVD算法），12个未知数共需要12个方程，即6对不共线的点对即可。若给定的点对多于6对，则变成最小二乘问题，可以同时求出一个最优的变换矩阵。

4、B样条变换（B-Spine Transformation）

B样条变换是一种基于B样条函数的非线性图像变换。

B样条函数的基本形式为：

$B(x)=\sum_{i=0}^{n}w_iN_{i,p}(x)$

这里 $w_i$ 是权重参数； $N_{i,p}(x)$ 是第i个B样条基函数，其中p是B样条函数的阶数，决定了平滑程度；n+1为权重参数的数量，并且n不小于p-1，不同的权重参数可以对应着不同的函数形状。（具体解释推荐一篇博文：(63条消息) 数值计算 --- B样条函数（B-spline）_松下J27的博客-CSDN博客）