排序算法之堆排序

排序算法之堆排序_20230624

news2024/10/6 20:30:54

排序算法之堆排序

前言

堆排序是基于比较排序的一类算法，算法重复利用堆(Binary heap)的特性，最大（最小）元素一定位于堆顶的位置，那么就可以提取堆顶元素，放置在数组的尾部位置，后再把剩余的元素进行堆处理，以此类推，最终完成排序任务。

堆定义

堆的定义如下，对于含有n个元素的序列
${k_1,k_2,k_3,....,k_n\}$
当且仅当满足下列关系时候，称之这个序列为堆（以大顶堆为例)，

在这里插入图片描述

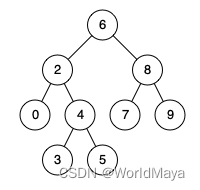
若将对应的此序列对应的一维数组看成是一个完全二叉树，则对的含义表明，完全二叉树中所有非终端节点的值均不小于其左、右孩子节点的值。由此，如果{k₁,k₂,…k_n}是堆，则堆顶元素必为序列中n个元素的最大值。具体看一个例子，下面的完全二叉树则是一个大顶堆。值得一提的是，大顶堆中最小元素则可能位于任意叶子节点中，它并没有特别的规律。

在这里插入图片描述

上面两个大顶堆都是符合要求的合格大顶堆，大顶堆中最小元素值为9，它可能位于第④或第⑤或第⑥个位置上。所以在大顶堆中，并不能确认完全二叉树中的最小值所在确切位置。

若在输出堆顶的最小值之后，使得剩余n-1个元素的序列重又建成一个堆，则得到n个元素中的次小值。如此反复执行，便能得到一个有序序列，这个过程便称之为堆排序(heap sort)

堆排序过程

综上所述，堆排序过程分为几个过程：

首先需要对输入的n无序元素进行大顶堆化处理
交换堆顶元素和序列中的最后一个元素
再对前n-1元素进行大顶堆化处理
交换堆顶元素和序列中最后一个元素
重复上述操作直至序列中仅剩一个元素（最小元素）

3-1 输入无序元素进行大顶堆化处理过程

给定数组元素arr={4,10,3,5,1}，要求通过完全二叉树建立大顶堆，过程如下，

在这里插入图片描述

可以观察到，上面的完全二叉树为大顶堆，通过交换堆顶元素和最后一个元素的值，交换发生后，堆中的元素数量减1,并重新对堆中的元素大顶化处理。

在这里插入图片描述

最终排序结果arr={1,3,4,5,10}

在这里插入图片描述

堆排序实现

4-1 对调整函数的实现

已知H.r[s…m]中记录的关键字除H.r[s]之外的均满足堆的定义要求，本函数调整H.r[s]关键字，使H.r[s…m]成为一个大顶堆。

void heap_adjust(HeapType *heap, int s, int m)
{
    int j;
    RcdType rc;
    rc=heap->r[s];

    for(j=2*s;j<=m;j=j*2)
    {
        if(j<m && LT(heap->r[j].key,heap->r[j+1].key))
        {
            j++;
        }

        //if rc.key is less than heap->r[j].key(j is larger between two values)
        if(!LT(rc.key,heap->r[j].key))
        {
            break;
        }

        heap->r[s]=heap->r[j];
        s=j;
    }

    heap->r[s]=rc;

    return;
}

4-2 堆排序实现

void heap_sort(HeapType *heap)
{
    int i;
    int n;
    RcdType rc;

    n=heap->length;

    for(i=n/2;i>0;i--)
    {
        heap_adjust(heap,i,n);
    }

    for(i=n;i>1;i--) //if there is one left(>1) and it had been sorted
    {
        rc=heap->r[i];
        heap->r[i]=heap->r[1];
        heap->r[1]=rc;

        heap_adjust(heap, 1, i - 1);
    }

    return;
}