题目：

链接：剑指 Offer 68 - I. 二叉搜索树的最近公共祖先；LeetCode 235. 二叉搜索树的最近公共祖先
难度：中等

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

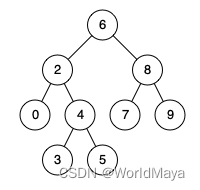
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

方法一：

根据二叉搜索树性质遍历：

已知在二叉搜索树中，对于一个节点，小于其节点值的节点一定在其左子树中，大于其节点值的节点一定在其右子树中，可得自顶向下的遍历搜索方法：

• 我们从根节点开始遍历；

• 如果当前节点的值大于 p 和 q 的值，说明 p 和 q 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；

• 如果当前节点的值小于 p 和 q 的值，说明 p 和 q 应该在当前节点的右子树，因此将当前节点移动到它的右子节点；

• 如果当前节点的值不满足上述两条要求，那么说明当前节点就是「分岔点」。此时，p 和 q 要么在当前节点的不同的子树中，要么其中一个就是当前节点。

代码一：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* ans = root;
        while(true) {
            if(ans->val > p->val && ans->val > q->val) ans = ans->left;
            else if(ans->val < p->val && ans->val < q->val) ans = ans->right;
            else break;
        }
        return ans;
    }
};

最坏时间复杂度O(N)，在二叉搜索树退化为链表时取得。
空间复杂度O(1)。

方法二：

搜索与回溯：

这个思路比较复杂，不考虑二叉搜索树的数值排序性质，直接找 p、q 节点，类似于后序遍历。用一个节点指针 *ans 记录找到的最近公共祖先。对于递归过程中的每个节点，先搜索它的左右子树中有没有 p 和 q ，在搜索左右子树的过程中，如果找到了 p 或 q ，会将 p 或 q 层层回溯传递，而如果已经找到了最近公共祖先ans，则直接将ans回溯传递；然后开始条件判断，如果已经在左右子树的搜索过程中找到了ans，那么直接回溯传递ans，如果root、左子树返回值 l 、右子树返回值 r 中有两个节点分别等于 p 和 q ，说明当前 root 就是最近公共祖先，赋值给 ans 并返回，如果root、l、r 中只有一个等于 p 或 q，则将这个节点回溯传递给上层判断，如果没找到 p 或 q 直接返回空值。

代码二：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    TreeNode *ans = nullptr;  // 最近公共祖先
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr) return nullptr;
        // 搜索左右子树
        TreeNode* l = lowestCommonAncestor(root->left, p, q);
        TreeNode* r = lowestCommonAncestor(root->right, p, q);
        // 条件判断
        if(ans != nullptr) return ans;
        bool pFound = (root == p || l == p || r == p);
        bool qFound = (root == q || l == q || r == q);
        if(pFound == true && qFound == true) {
            ans = root;
            return ans;
        }
        if(pFound == true) return p;
        if(qFound == true) return q;
        return nullptr;
    }
};

时间复杂度O(N)。
空间复杂度O(N)，取决于递归栈空间，在二叉搜索树退化为链表时取得。