1、约束编程求解器

$\qquad$ 约束编程是一种编程范式，旨在解决那些需要满足一系列约束条件的问题。在约束编程中，问题被定义为一组变量和约束条件，而不是指定解决问题的算法步骤。通过定义变量之间的关系和约束条件，约束编程系统能够自动找到满足所有约束条件的解。
$\qquad$ 在约束编程中，变量通常定义在一个特定的域中，该域包含了变量可能的取值范围。约束条件定义了变量之间的关系，可以是等式、不等式、逻辑关系等。这些约束条件可以是显式指定的，也可以是通过问题的规范隐含地定义的。
$\qquad$ 约束编程的求解器使用各种算法和技术来搜索满足所有约束条件的解。这些算法可以是基于回溯的，通过尝试不同的变量赋值和约束条件的满足程度来逐步搜索解空间。还可以使用启发式搜索、优化算法等方法来加速搜索过程。
$\qquad$ 约束编程可以应用于各种领域和问题，如排程问题、资源分配、路线规划、布局设计等。它的优势在于可以简化问题的建模过程，提供一种声明式的方式来描述问题，而不需要指定详细的求解步骤。此外，约束编程还能够处理复杂的约束条件和大规模问题。
$\qquad$ 一些常见的约束编程语言和工具包括Prolog、ECLiPSe、MiniZinc、Choco等。这些工具提供了丰富的约束库和求解器，可以帮助开发人员更轻松地建模和求解约束问题。
$\qquad$ 下面通过一个女娲补天问题来直观理解约束编程。
在这里插入图片描述
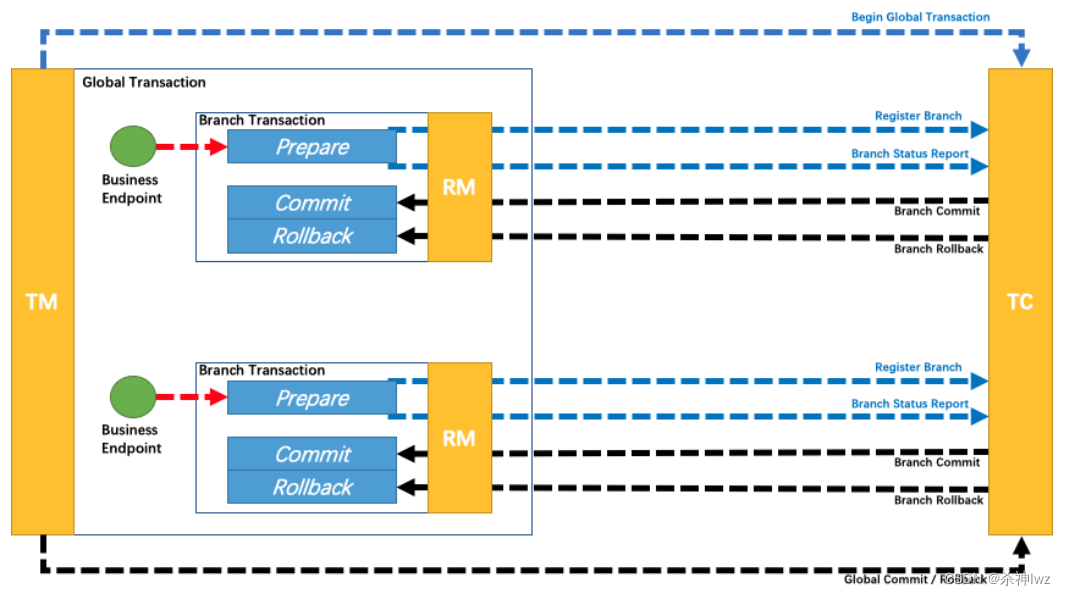
$\qquad$ 在一个9×9的矩阵中有一些数字和一些空格，需要在空格中填上1-9数字中的一个，使得每一行不能出现重复数字；每一列不能出现重复数字，每一个3×3的小方格中不能出现重复数字。这时候使用约束编程可以设定一个变量 $y_{i,j}$ 表示每一个小格 $i$ 是否放某个数字 $j$ ，之后通过约束推理和传播，解方案搜索(猜测)的方法一步步找到可行解，若某次搜索过程中无法找到可行方案，则回溯并撤回之前做的决定。重复上述过程，直到找到可行解，输出结果。从而可以知道约束编程的核心组成部分便是约束传播和搜索。
$\qquad$ 约束传播时，需要一次检查每一个约束，分析约束中的变量的可能数值并减少变量的可行域，重复上述过程知道没有进一步减少变量可行域的可能。
$\qquad$ 搜索时，需要通过猜测做出一个决定，之后将这个决定的影响在不同的约束中进行传播。重复上述过程，直至找到一个解或者失败(某些约束不能满足)，若出现失败的情况，则需要回溯到之前做过的决定，并撤回改用其他决定。

2、值域+传播器

$\qquad$ 值域：代表变量的可能数值。每一个变量 $X$ 的值域记作 $D (X)$ ，通常 $D (X)$ 是有限的，但可能回非常大。实质上，每一个变量 $X$ 代表了一个选择(猜测)，值域 $D (X)$ 代表了 $X$ 的可能选择。当 $D(X)=\empty$ 时，表示当前变量没有可行域。
$\qquad$ 赋值：一个赋值 $\theta$ 表示从变量到数值的映射，例如 $\{X\rightarrow3, Y\rightarrow 4\}$ 可以记作： $\theta(X)=3, \theta(Y)=4, vars(\theta)=\{X,Y\}$ 。若对于每一个 $X\in vars(\theta)$ 均满足 $\theta(X)\in D(X)$ ，则称一个赋值 $\theta \in D$ 。
$\qquad$ 一个解：是一个能够满足问题中所有约束的赋值。
$\qquad$ 赋值域： $D_{\theta}(X)=\{theta(X)\}, X \in vars(\theta)$
$\qquad$ 一个约束： $C$ 是一个对变量集合 $v a rs (C)$ 的赋值集合(约束的解)，如下示例所示：
在这里插入图片描述
$\qquad$ 传播器：一个传播器代表一个约束；可以利用传播器推断出在当前给定的值域下，变量的哪些数值是不可行的。
$\qquad$ 一个关于约束 $C$ 的传播器是一个从值域映射到另外一个值域的函数： $D^{'} = f (D)$ ；
$\qquad$ 传播器需要满足以下性质：

单调递减：即传播器只能加约束的值域变得越来越小，不能增大约束的值域： $\subseteq D(X)$
正确性：不会从 $D$ 中移除一个将会出现在约束 $C$ 的解中的数值，如若 $\theta$ 是C中某个变量的映射， $\theta \in D$ ，则一定需要满足 $\theta \in f(D)$
检查性：当某个约束 $C$ 中所有的变量都被固定了，那么传播器会返回一个空的值域；若被固定的所有变量恰好可以组成约束 $C$ 的解，则传播器返回这个解，即 $f(D_{\theta})=D_{\theta}$ 当且仅当 $\theta$ 是 $C$ 的一个解。
$\qquad$ 如下是一个传播器的例子：

$\qquad$ 值域传播器：对于约束 $C$ ，最强的传播器会移除值域 $D$ 中所有不属于 $C$ 的解的值，称这种最强的传播器为值域传播器，记为 $f(D)(X)=D(X)\cap \{\theta(X)|\theta \in C, \theta \in D\}$
$\qquad$ 支持和域相容：给定任意的 $X_i \in vars(C)$ ，对全部的 $v_i \in D(X_i)$ ，在 $C$ 的其他变量中均存在 $v_j \in D(X_j)$ ，使得 $\theta \in C$ ，则 $v_j$ 被称作 $v_i$ 的支持。约束 $C$ 中所有变量均满足上述要求时，则称约束 $C$ 的变量之间域相容。下面是一个值域传播器的示例：

$\qquad$ 对于线性方程 $\sum_i a_iX_i=b$ 来说，设计一个值域传播的时间复杂度是一个 $NP$ 难的问题；但是对于一个线性不等式 $\sum_i a_iX_i\leq b$ 来说，设计一个值域传播器的时间复杂度为 $O (n)$ 。