目录

一、列出物资调运平衡表和运价表

二、编制初始调运方案

三、初始方案的检验与调整 

 1）闭合回路法

 2）位势法

 3）调整调运方案 

表上作业法一般步骤： 

①列出调运物资的供需(产销)平衡表及运价表；

②按最小元素法建立初始调运方案；

③采用位势法计算初始方案每个空格的闭回路的检验数Dxij ；

④检查检验数，如果所有Dxij >=0，说明方案是最优的，已经得到我们想要的方案，结束求解；

⑤如果有某个或某几个Dxij<0，则选择负检验数中绝对值最大的闭回路进行调整，建立新的方案；

⑥重复3—5步，直至获得最优调运方案。

表上作业法的实质就是利用运价表在平衡表上进行求解。 

例题：某公司下属三个储存某种物资的仓库，供应四个工地的需要。三个仓库的供应量和四个工地的需求量以及由各仓库到各工地调运单位物资的运价(元／吨)由下表给出，试求运输费用最少的调运方案。

一、列出物资调运平衡表和运价表

供需平衡表

二、编制初始调运方案

        物资调运规划其总目的是寻求一个运输费用最少的最优调运方案。一般最优方案是由初始方案经过反复调整得到的。因此，编制出较好的初始调运方案非常重要。

        最好的调运方案是使运费最省的方案，因此可以用最小元素法来确定初始调运方案。

        最小元素法，就是按运价表依次挑选运费少的供——需点尽量优先安排供应的调运方法。

---

        ①首先，在运价表内找出最小的运价，对本例而言，方格(2，1)数值是1，最小，这样，供应点A2尽可能地满足B1工地的需要，于是在平衡表中有(2，1)＝300，即在空格(2，1)中填入数字300。  

        此时，由于工地B1已经全部得到满足，不需要其他仓库供应给它了，运价表中的第一列数字已不起作用，因此将运价表第一列划去，并标注符号①，

        相应地，由于仓库A2所储物资已全部供应完毕，因此，在运价表中与A2同行的运价也不再起作用，所以也将它们划去，并标注符号②。 

---

        ③仿照前面的方法，一直作下去，就得到如下图所示的运价表和平衡表。 

(1，4)＝300。这样就得到表4的初始调运方案。

        ④根据初始调运方案的运输量和单位运价，可以计算初始调运方案的运输费用为：

    S=1*300+4*600+3*400+2*100+10*300+5*300=8600(元)

三、初始方案的检验与调整 

 1）闭合回路法

    闭回路：对表上作业法的初始方案，从调运方案表上的一个空格出发，存在—条且仅存在一条以该空格(用 xij 表示)为起点，以其他填有数字的点为其他顶点的闭合回路，简称闭回路。

 空格(1，1)：  (1，1)—(1，3)—(2，3)—(2，1)一(1，1)

 空格(3，1)：  (3，I)—(2，1)—(2，3)—(1，3)一(1，4)—(3，4)—(3，1)

对所有的空格，都可以用同样的方法画出一条闭回路。

  检验数：调运方案的每个空格所形成的闭回路上，作单位物资的运量调整，总可以计算出相应的运费是增加还是减少。把所计算出来的每条闭回路上调整单位运量而使运输费用发生变化的增减值，称其为检验数。

最优方案的判定准则：

     初始调运方案中，如果它所有的检验数都是非负的，那么这个初始调运方案最优。否则。这一调运方案不一定是最优的。

   （如果所有空格的检验数都小于零，那么如果再对调运方案进行任何调整，都会增加运输费用）

2）位势法

第一步：求位势量

        首先将初始调运方案中填有运量的方格对应的运价填写好，然后将初始调运方案中填有运量的方格对应的运价cij分解为两部分，即：  

    cij =ui+vj ,(i=1,2,3; j=1,2,3,4，这里的i和j均为下标，下同)

其中ui和vj 分别为该方格对应于i行和j列的位势量.

然后列出所有方程

假定其中一个未知量为0（任意），如假定v1=0,则可以根据方程解出全部未知量。 

第二步：求准检验数 

第三步：求检验数 

        利用运价表与准检验数表求检验数

 

检验结果：检验数出现负值，根据最优方案判断准则，该方案不是最优方案。

    3）调整调运方案 

调整过程：

（1）作出负值所在空格的闭回路，本例为空格x24，闭回路如上图所示。

（2）沿闭回路在各奇数次转角点中挑选运量的最小数值作为调整量。本例是将x23方格的100作为调整量，将这个数填入空格x24内，同时调整该闭回路中其他转角点上的运量，使各行、列保持原来的供需平衡．这样使得到一个新的调运方案。

调整后的结果如下

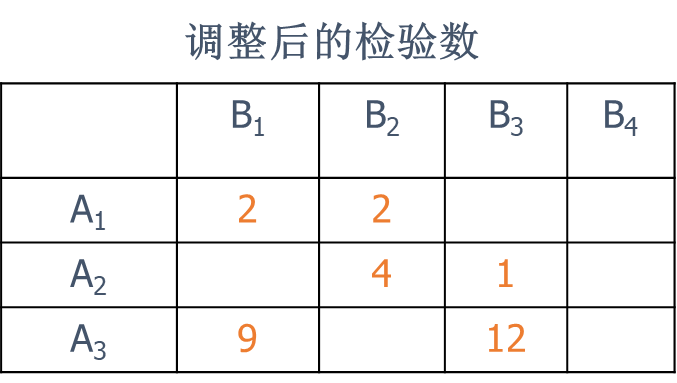
通过计算其检验数全部非负，此方案为最优方案。

运输费用为：S＝3×500十10×200十8×100十1×300十4×600十5×300＝8500(元)

该值小于初始调运方案的总运费。