魔方有 3 种不同的方块,分别为角块(8 个,每个角块有三种颜色),棱块(12 个,每个棱块有两种颜色)与中心块(6 个,每个中心块有一种颜色)。
魔方总共有 6 个面,每个面的颜色不一样,每个面被分为 9 个小面,我们称小面为 facelets,魔方总共有 54 个 facelets.
问题来了:魔方有多少种状态?
先给出答案:

为什么是这个数字呢?
三阶魔方总变化数可利用乘法原理计算,具体方法是:
-
8 个角块可以互换位置(8!),也可以旋转(3),所以分子里有 8 ! ∗ 3 8 8! * 3^{8} 8!∗38
-
但不能单独翻转一个角块,也就是说当前面 7 个角块都确定方向后,最后一个角块的方向也就确定了,所以分母有个 3
-
12 个棱块可以互换位置(12!),也可以翻转(2),所以分子里有 12 ! ∗ 2 12 12! * 2^{12} 12!∗212
-
但不能单独翻转一个棱块(也就是将其两个面对调),当前面 11 个棱块都确定方向后,最后一个棱块的方向就确定了,所以分母有个 2
-
你会发现分母里还有个 2,这是为什么呢?因为奇偶性。
角块和棱块同奇同偶
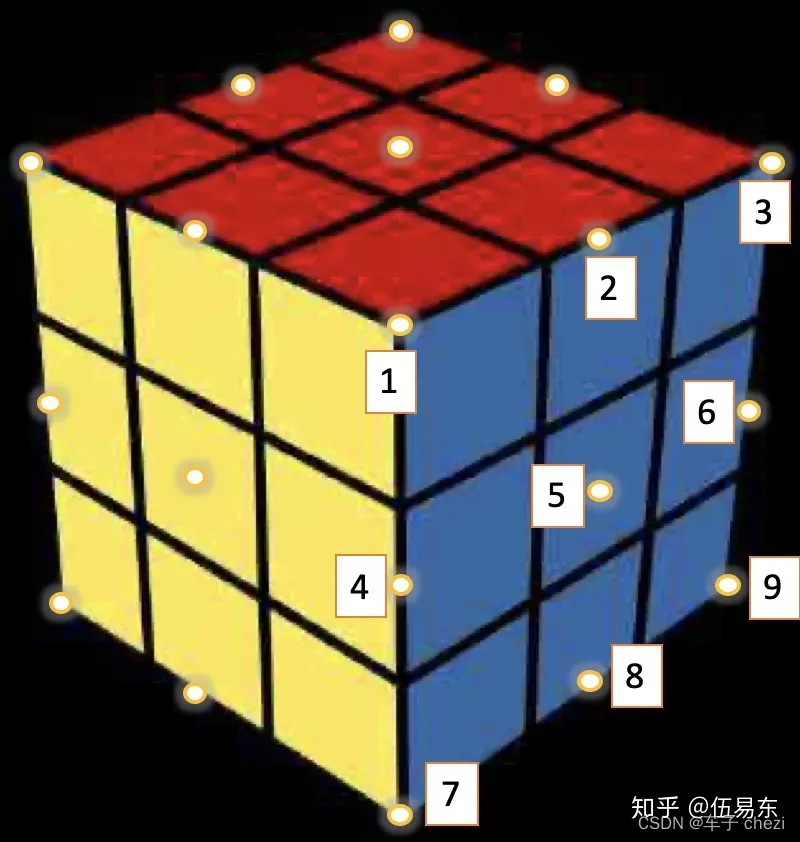
看这个魔方,我们以顺时针旋转蓝色的面为例子
对于角块,顺时针看,本来是 1 3 9 7,旋转后变成 7 1 3 9;
把这个变化拆解一下:
- 7 和 1 交换:7 3 9 1
- 1 和 9 交换:7 3 1 9
- 3 和 1 交换:7 1 3 9
也就是交换了 3 次,3 是奇数;同理,棱块的交换也是 3 次
不管旋转哪个面,只要是单次转动,对于角块和棱块都是奇置换,多次转动复合起来,角块和棱块的奇偶性会保持一致。(注意:两个偶置换的复合是偶的;两个奇置换的复合是偶的;一个奇置换与偶置换的复合是奇的)
所以,不可能仅交换一对角块,也不可能仅交换一对棱块。假设你给 8 个角块和前面 10 个棱块都安排好了位置,那这剩余的 2 个棱块,其位置是确定的:如果角块是奇置换(或偶置换),那这剩余的 2 个棱块要和前面的棱块凑成奇置换(或偶置换)。
于是分母还有一个 2,因为剩余的 2 个棱块在位置上没有选择。
不能单独翻转一个棱块
既然了解了偶置换和奇置换,那我们想一想为什么不能单独翻转一个棱块。
假设给 12 个棱块的每个面都标上序号(1~24),在单步转动中,其实是 2 组奇置换,复合起来是偶置换。多次转动复合起来,还是偶置换。而单独翻转一个棱块,是奇置换,所以不可能。
不能单独翻转一个角块
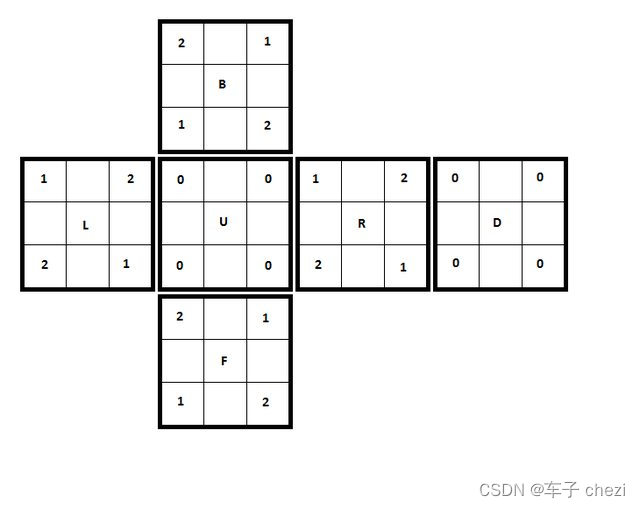
如图所示,我们给每个角块的 3 个小面都标上 0,1,2,这是初始状态。注意,对于每个角,沿魔方的体对角线看入时,是一个 Y 字型,0 在最上面,1 在左边,2 在右边
我们规定,角块的方向值是它在 U 面或者 D 面的数字。
对于 U 和 D 面,不管怎么转,角块的方向都不改变。
对于其他 4 个面,顺时针或逆时针转动的效果都一样,我们只需要研究一个面,例如 F:
我们把 F 面顺时针转动 90 度,看看受影响的 4 个角块的方向值增加了多少。
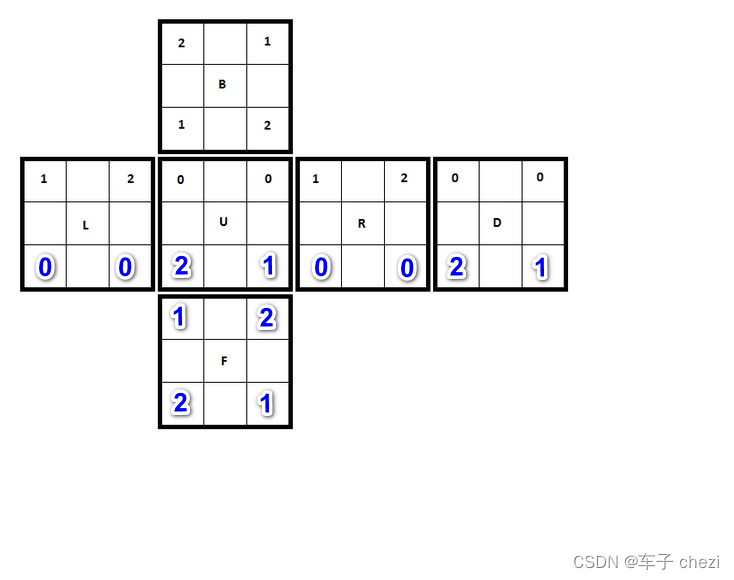
可以看到,4 个角块分别增加 2,1,2,1,这说明什么呢?
说明有 2 个角块逆时针旋转了 120°,另外 2 个角块顺时针旋转了 120°,这 4 个角块一共旋转了 0°
其他情况是类似的,我们就不分析了。
因此可以推出,不管魔方怎么转,8 个角块的方向值之和都是 0
所以不可能单独翻转一个角块,一个角块翻转了,必然伴随其他的角块也翻转,来维持方向值之和是 0
【完】
参考资料
【1】魔方中的数学2-置换的定义 - 知乎
【2】Why is a single-corner twist not a valid position on a Rubik’s cube? - Puzzling Stack Exchange
【3】为什么魔方在转动一个角块后无法复原?作者:鸿鹄