本文介绍了PEFT中Selective Methods的DiffPruning、 BitFit；重参数化方法中的LoRA和AdaLoRA；以及混合方法中的MAM Adapters和UniPELT。分类方法见PEFT综述论文《Scaling Down to Scale Up: A Guide to Parameter-Efficient Fine-Tuning》

四、Selective Methods

参考论文《Scaling Down to Scale Up: A Guide to Parameter-Efficient Fine-Tuning》

  选择性方法是对模型的现有参数进行微调的一种方法。可以根据层的深度、层的类型，甚至是某个参数进行选择。

4.1 DiffPruning（2020.10）

• 论文《Parameter-Efficient Transfer Learning with Diff Pruning》
• 知乎《Diff Pruning: 一种参数高效的迁移学习新方法》

  Adapter Tuning通过在模型的层之间插入针对特定任务的残差模块，并只优化这些残差模块。由于残差模块的参数更少（约3.6%），因此微调成本更低。

  本文提出的 Diff pruning 与Adapters类似，但 Diff pruning 不是修改模型的结构，而是通过一个特定任务的 diff 向量扩展基础模型，只需要微调0.5%的预训练参数，即Diff pruning 将特定任务的微调表述为学习一个 diff 向量${\delta }_{\tau }$，该向量被添加到预先训练的模型参数${\theta }_{pretrained}$（固定）中 ：
$${\theta }_{task}={\theta }_{pretrained}+{\delta }_{task}$$

差异向量用L0-norm惩罚的可微近似值进行重构，以鼓励稀疏性（详见知乎贴）。

  prompt tuning是微调一个soft prompt tokens，而DiffPruning也是冻结大部分语言模型参数只微调一个插入的diff向量，本质上是一样的。

4.2 BitFit（2021.6）

• 论文《BitFit: Simple Parameter-efficient Fine-tuning for Transformer-based Masked Language-models》
• 知乎《大模型参数高效微调技术原理综述（二）-BitFit、Prefix Tuning、Prompt Tuning》

理想状况下，我们希望有一种满足以下条件的高效微调方法：

• 到达能够匹配全量微调的效果。
• 仅更改一小部分模型参数。
• 使数据可以通过流的方式到达，而不是同时到达，便于高效的硬件部署。
• 改变的参数在不同下游任务中是一致的。

  Ben-Zaken等人（2021年）提出仅对网络的偏置进行微调。也就是说，在每个线性或卷积层中，权重矩阵W保持不变，只优化偏置向量b，伪代码如下：

params = (p for n, p
		in model.named_parameters()
		if "bias" in n)
optimizer = Optimizer(params)

  BitFit仅更新模型参数的约0.05%。原始论文证明了该方法在BERT模型（小于10亿个参数）中在低数据和中等数据情况下实现了类似或更好的性能。但在更规模更大的网络上，如T0-3B或GPT-3，BitFit效果低于fine-tuning和其他PEFT方法。

  对于Transformer模型而言，冻结大部分 transformer-encoder 参数，只更新bias参数跟特定任务的分类层参数。涉及到的bias参数有attention模块中计算query,key,value跟合并多个attention结果时涉及到的bias，MLP层中的bias，Layernormalization层的bias参数。

  通过在Bert-Large模型上基于GLUE数据集进行了 BitFit、Adapter和Diff-Pruning的效果对比，可以发现：

• BitFit在参数量远小于Adapter、Diff-Pruning的情况下，效果与Adapter、Diff-Pruning相当，某些任务上甚至更优。
• BitFit微调结果虽不及fine-tuning，但是远超固定全部模型参数的Frozen方式。

  同时，通过对比BitFit训练前后的参数，发现只有计算query以及FFN层的第一层（特征维度从N放大到4N）的bias参数变化最为明显，只更新这两类bias参数也能达到不错的效果，反之，固定其中任何一者，模型的效果都有较大损失。

4.3 Freeze and Reconfigure (FAR，2022)

  FAR（Vucetic等人，2022年）选择参数矩阵的列进行剪枝，并将线性层重新配置为可训练和冻结的状态。该方法分为两个阶段。

• 阶段一：确定参数矩阵中最重要的行进行更新。这个过程类似于结构化剪枝，并可以使用任何剪枝方法。
• 阶段二：将每个参数$W$拆分为可训练部分$W_t$和冻结部分$W_f$，对偏置也执行类似的操作，然后将结果连接起来，重新配置网络。

整个方法伪代码如下：

def far_layer(x):
	h1 = x @ W_t 	# W_t为可训练部分参数
	h2 = x @ W_f 	# W_f为冻结部分参数
	return concat([h1, h2], dim=-1)

  原始论文主要关注边缘场景，并在实验中使用了DistilBERT（66M）。FAR仅应用于前馈层，因为这些层占据了DistilBERT参数的大部分。作者表明，FAR在五个GLUE任务和SQuAD 2.0（Rajpurkar等人，2018年）上更新了6%的参数，并实现了与微调相似的性能。

4.4 FishMask（略）

五、Reparametrization-based methods（重参数化）

5.1 Intrinsic SAID（2020.12）

《Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning》

  虽然预训练语言模型可以通过微调在广泛的语言理解任务中产生最先进的结果，但这一过程的动态性尚不完全了解，特别是在低数据情况下。为什么我们可以使用相对传统的梯度下降算法（例如，没有强正则化）来微调具有数亿参数的模型，并仅使用数百或数千个标记示例的数据集？

  在Aghajanyan等人（2020年）的工作中，他们证明了常见的预训练模型具有非常低的内在维度，故存在一种低维度的重新参数化方式，使微调效果媲美fine-tuning。

  具体而言，他们使用Fastfood变换重新参数化模型权重的更新。他们的结果表明，与较小的模型相比，较大的模型需要在较低秩子空间中进行变化才能达到相同的微调性能。这个观察结果激发了对大型模型和参数效率微调的关注

  虽然可以优化的参数数量较低，但Fastfood的内存复杂度以及对所有模型参数的更新使得Intrinsic SAID在微调大型网络方面不实用。

5.2 LoRa（2021.6）

《LoRA: Low-Rank Adaptation of Large Language Models》、Microsoft/LoRA、stanford_alpaca

5.2.1 背景

  神经网络包含许多稠密层，这些层执行矩阵乘法。这些层中的权重矩阵通常具有满秩。Intrinsic SAID的研究表明，尽管预训练模型的参数量很大，但每个下游任务对应的Intrinsic Dimension（本征维度）并不大，即使在随机投影到较小子空间时，仍然可以有效学习。换句话说，理论上我们可以微调非常小的参数量，就能在下游任务取得不错的效果。

  受此启发，我们假设权重的更新在适应过程中也具有较低的intrinsic rank（内在秩）。对于一个预训练的权重矩阵$W_0\in {\mathbb{R}}^{d\times k}$，我们不直接微调$W_0$，而是微调一个增量$\Delta W$来更新模型。

5.2.2 算法

  具体来说，在原始的预训练模型PLM旁边增加一个新的通路（相当于一个外挂），通过前后两个矩阵A,B相乘，来模拟本征秩。外挂层和预训练模型层维度都为d，第一层会先将维度d通过全连接层降维至r，第二层再从r通过全连接层映射回d维度，其中，r<<d。

  这里的r是矩阵的秩，这样矩阵计算就从d x d变为d x r + r x d，参数量减少很多，这一步就叫做低秩分解。

图1：重参数化，只训练A和B

添加外挂层后，前向传播用公式来表示就是：
$$h=W_{0}x+\Delta Wx=W_{0}x+BAx$$

其中$W_0\in {\mathbb{R}}^{d\times k}$，$B\in {\mathbb{R}}^{d\times r}$，$A\in {\mathbb{R}}^{r\times k}$。

整个过程用伪代码表示就是：

def lora_linear(x):
	h = x @ W 			
	h += x @ W_A @ W_B  # 低秩分解
	return scale * h    # sacle为缩放因子，等于1/r

  第一个矩阵的A的权重参数会通过高斯函数初始化，而第二个矩阵的B的权重参数则会初始化为零矩阵，这样能保证训练开始时新增的通路BA=0从而对模型结果没有影响。

  在推理时，将左右两部分的结果加到一起即可，$h=W_{0}x+BAx=(W_0+BA)x$，所以只要将训练完成的矩阵乘积$BA$跟原本的权重矩阵$W_0$加到一起作为新权重参数替换原本PLM的$W_0$即可，对于推理来说，不会增加额外的计算资源。

5.2.3 实验

1. 对比其它PEFT方法的效果

表2：RoBERTa base，RoBERTa large和DeBERTa XXL在GLUE基准测试中使用不同的适应方法。我们报告了MNLI的整体（匹配和不匹配）准确率，CoLA的Matthew相关系数，STS-B的Pearson相关系数以及其他任务的准确率。所有指标都越高越好。*表示在之前的研究中发布的数字。†表示在设置类似于Houlsby等人（2019）的运行配置中进行了公平比较。

表3：使用不同的适应方法对GPT-2中型（M）和大型（L）模型在E2E NLG挑战赛上的表现。对于所有指标，数值越高越好。LoRA在可比较或更少的可训练参数情况下优于几个基线模型。我们运行的实验显示了置信区间。*表示在之前的研究中发布的数字。

2. 微调权重选择

Transformer的权重矩阵包括：

• Attention模块：
  • 计算query, key, value的$W_q$，$W_k$，$W_v$
  • 用于多头attention计算结果$hea{d}_1...hea{d}_n$拼接时的矩阵$W_o$
• MLP层的权重矩阵

  LoRA只应用于Attention模块中的4种权重矩阵，而且通过消融实验发现同时调整 $W_q$ 和 $W_v$ 会产生最佳结果。

  另外，保证权重矩阵的种类的数量比起增加隐藏层维度r更为重要，增加r并不一定能覆盖更加有意义的子空间。

3. 秩的选择，通常选4、8、16即可。

表18：LoRA在使用GPT-2 Medium模型时，根据不同的秩r在E2E NLG Challenge上实现的验证损失和测试集指标。与在GPT-3上r = 1适用于许多任务不同，在这里验证损失的性能在r = 16时达到峰值，而BLEU指标在r = 4时达到峰值，这表明GPT-2 Medium在适应性方面与GPT-3 175B具有类似的内在秩。请注意，我们的某些超参数是在r = 4上进行调整的，这与另一个基线的参数数量相匹配，因此对于其他r的选择可能不是最优的。

5.3 AdaLoRA（2023.3）

论文《Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning》、QingruZhang/AdaLoRA

5.3.1 背景

之前的Adapter tuning方法和下游任务增量的方法都存在一些问题：

• 添加小型网络模块：将小型网络模块添加到PLMs中，保持基础模型保持不变的情况下仅针对每个任务微调这些模块，可以用于所有任务。这样，只需引入和更新少量任务特定的参数，就可以适配下游的任务，大大提高了预训练模型的实用性。如：Adapter tuning、Prefix tuning、Prompt Tuning等。这类方法虽然大大减少了内存消耗。但是这些方法存在一些问题，比如：Adapter tuning引入了推理延时；Prefix tuning或Prompt tuning直接优化Prefix和Prompt是非单调的，比较难收敛，并且消耗了输入的token。
• 下游任务增量更新：对预训练权重的增量更新进行建模，而无需修改模型架构，即W=W0+△W。比如：Diff pruning、LoRA等， 此类方法可以达到与完全微调几乎相当的性能，但是也存在一些问题，比如：Diff pruning需要底层实现来加速非结构化稀疏矩阵的计算，不能直接使用现有的框架，训练过程中需要存储完整的∆W矩阵，相比于全量微调并没有降低计算成本。 LoRA则需要预先指定每个增量矩阵的本征秩 r 相同，忽略了在微调预训练模型时，权重矩阵的重要性在不同模块和层之间存在显著差异，并且只训练了Attention，没有训练FFN，事实上FFN更重要。

基于以上问题进行总结：

1. 我们不能预先指定矩阵的秩，需要动态更新增量矩阵的R，因为权重矩阵的重要性在不同模块和层之间存在显著差异。
2. 需要找到更加重要的矩阵，分配更多的参数，裁剪不重要的矩阵。找到重要的矩阵，可以提升模型效果；而裁剪不重要的矩阵，可以降低参数计算量，降低模型效果差的风险。

  为了弥补这一差距，作者提出了AdaLoRA，它根据权重矩阵的重要性得分，在权重矩阵之间自适应地分配参数预算。

5.3.2 算法

AdaLoRA是对LoRA的一种改进，它根据重要性评分动态分配参数预算给权重矩阵。具体做法如下：

• 调整增量矩分配。AdaLoRA将关键的增量矩阵分配高秩以捕捉更精细和任务特定的信息，而将较不重要的矩阵的秩降低，以防止过拟合并节省计算预算。
• 以奇异值分解的形式对增量更新进行参数化，并根据重要性指标裁剪掉不重要的奇异值，同时保留奇异向量。由于对一个大矩阵进行精确SVD分解的计算消耗非常大，这种方法通过减少它们的参数预算来加速计算，同时，保留未来恢复的可能性并稳定训练。

$$W=W^{(0)}+∆=W^{(0)}+P\Lambda Q$$

其中，$P\in {\mathbb{R}}^{d_1\times r}$，$Q\in {\mathbb{R}}^{r\times d_2}$，表示$\Delta$的左/右奇异向量。对角矩阵$\Lambda \in {\mathbb{R}}^{r\times r}$。

• 在训练损失中添加了额外的惩罚项，以规范奇异矩阵P和Q的正交性，从而避免SVD的大量计算并稳定训练。

5.3.3 实验

  通过实验证明，AdaLoRA 实现了在所有预算、所有数据集上与现有方法相比，性能更好或相当的水平。 例如，当参数预算为 0.3M 时，AdaLoRA 在RTE数据集上，比表现最佳的基线（Baseline）高 1.8%。

表1：在GLUE开发集上使用DeBERTaV3-base的结果。每个数据集上的最佳结果以粗体显示。我们报告了STS-B的平均相关性。Full FT、HAdapter和PAdapter分别代表完全微调、Houlsby适配器和Pfeiffer适配器。我们报告了使用不同随机种子进行的5次运行的平均值。

表2：在SQuAD v1.1和SQuAD v2.0上使用DeBERTaV3-base的结果。这里的# Params是相对于完全微调中的可训练参数数量。我们报告EM/F1。每个设置中的最佳结果以粗体显示。

六、混合方法

6.1 SparseAdapter（略）

6.2 MAM Adapters（2021.10）

• 论文《Towards a Unified View of Parameter-Efficient Transfer Learning》
• 参考《论文阅读：对参数高效迁移学习的统一看法》、知乎《大模型参数高效微调技术原理综述（六）-MAM Adapter、UniPELT》

6.2.1 背景

  最近的研究提出了多种参数高效的迁移学习方法，只微调少量（额外的）参数即可达到强大的性能。尽管这些方法有效，但对于成功的关键因素以及各种方法之间的联系了解甚少。

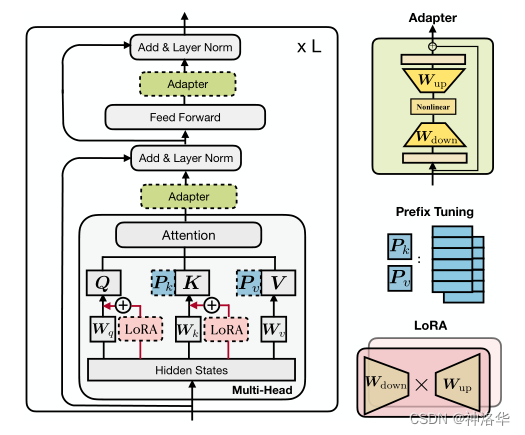
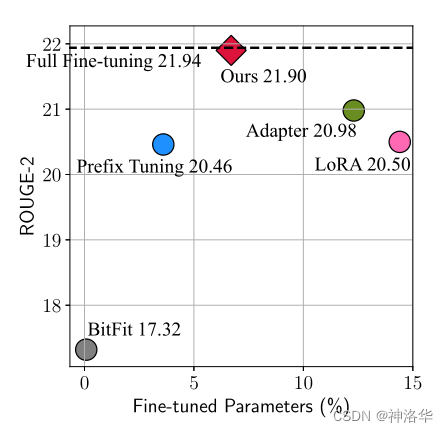
  例如下图展示了不同的微调方法，在Xsum数据集上做英文文本摘要任务的效果（ROUGE-2是该任务的评价指标（越大越好））以及其他高效微调方法参数量相对于全参数微调参数量的百分比。图中的左上角的位置是理想化的方法，从图中发现，Adapter,Prefix Tuning,LoRA都是性能比较好的方法。

图1：展示了Transformer架构和一些最先进的参数高效调整方法。我们使用带虚线边界的块来表示这些方法添加的模块。	图2：不同方法在XSum摘要任务上的性能。

这三种方法的数学表示整理如下：

  为什么看起来Adapter,Prefix Tuning,LoRA（在结构上和公式上）都不太一样，尤其是Prefix Tuning，但是这三种方法有近似的效果？

6.2.2 Prefix Tuning的进一步研究

  Prefix Tuning在每个层的多头注意力中，在key和value的前面添加了l个可调节的前缀向量。具体来说，两组前缀向量$P^k,P^v\in {\mathbb{R}}^{l\times d}$与原始键K和值V进行连接。然后在新的前缀键和值上执行多头注意力计算。多头注意力的第i个头的计算变为：

  Prompt-tuning是通过仅在第一层前缀输入词嵌入来简化了前缀调整；类似的工作还包括P-tuning。下面作者推导出了公式5的等效形式，并提供了前缀调整的另一种观点。

  其中，λ(x)是一个标量，表示前缀上归一化注意力权重的总和。公式7中的第一项$Attn(x{W}_q,C{W}_k,C{W}_v)$，是没有前缀的原始注意力，而第二项是独立于C的逐位置修改。公式7提供了前缀调整的另一种观点，它基本上通过线性插值对原始的头部注意力输出h进行逐位置修改：

我们重新定义$W_1=W_q{P}_k^T,W_2=P_v,f=softmax$，重写公式9则有：

  这种观点得出的公式与Adapter的公式$h\leftarrow h+f(h\cdot W_{down})\cdot W_{up}$非常相似，只是前缀调整执行的是加权相加，而适配器不进行加权。图3b展示了从这个视角看前缀调整的计算图，它允许将前缀调整抽象为类似适配器的插件模块。

  此外，我们注意到当l很小时，$W_1\in {\mathbb{R}}^{d_h\times l}$和$W_2\in {\mathbb{R}}^{l\times d_h}$是低秩矩阵，因此它们在功能上与适配器中的$W_{down}$和$W_{up}$矩阵类似。这种观点还表明，前缀向量的数量l在适配器中扮演类似瓶颈维度r的角色：它们都表示修改向量∆h计算时的秩限制。因此，我们将l也称为瓶颈维度。

秩限制意味着对于任何x，∆h都是同样的l（或≤l）个基向量的线性组合。

6.2.3 PEFT的统一框架

  上一节，通过对Prefix Tuning变换，发现Prefix Tuning和Adapters的公式高度相似。进一步的 ，作者对最先进的PEFT方法进行了解构，并提出了一个统一的框架来建立它们之间的联系。具体而言，我们将它们重新定义为对预训练模型中特定隐藏状态的修改（修改∆h），并定义了一组设计维度，包括计算修改的函数和应用修改的位置等，这些维度在不同方法之间存在变化。

  下图分析不同微调方法的内部结构和结构插入形式的相似之处。下图展示了高效微调方法Adapter、Prefix Tuning、LoRA以及新变体（通过更换一些元素，设计了前人的工作里没有的变体） Parallel Adapter、 Scaled PA的结构。

图3：现有方法和提出的变种的图形说明。"PLM模块"表示PLM（例如注意力或前馈网络）的某个子层被冻结。"Scaled PA"表示缩放的并行适配器

  下表展示了高效微调方法Adapter、Prefix Tuning、LoRA以及新变体在各个维度的对比。

• ∆h functional form：计算∆h的具体函数，这部分是需要学习的部分。所有这些方法的函数形式都类似于projdown→nonlinear→projup架构，而 nonlinear 在LoRA中退化为特征函数。
• Insertion form：添加模块的结构插入形式
• modified representation：新增结构在PLM修改的具体位置
• composition function：指修改后的向量∆h如何与原始的隐藏表达h组成，以形成新的隐藏表达。例如，适配器执行简单的加法合成，prefix tuning使用门控加法合成，而LoRA通过一个恒定的因子来缩放∆h，并将其添加到原始隐藏表示中

  其中，新增可训练参数结构形式为需要学习的部分（注：Prefix Tuning为经过转换后的格式）；插入形式有串联或并联；模型修改的具体位置有Attention、FFN层。

  这个统一的框架使我们能够沿着这些设计维度研究参数有效的微调方法，确定关键的设计选择，并有可能在不同的方法之间转移设计元素。基于此，我们能够实现新的参数高效微调方法MAM Adapters，其微调的参数比先前方法少，同时更加有效，在所有四个任务上实现了与微调所有参数相当的结果。

6.2.4 转移设计元素

  在图3中及表1中，我们设计了几个新的方法，这些方法可以通过我们上面的统一观点，在不同的方法之间转移设计元素而得到：

• Parallel Adapteris：通过将prefix tuning的平行插入转移到适配器的变体。 有趣的是，虽然我们因其与prefix tuning的相似性而提出了Parallel Adapteris，但同时进行的工作独立地提出了这个变体并对其进行了经验研究
• Multi-head Parallel Adapter：使适配器与prefix tuning更加相似的进一步措施：我们应用Parallel Adapteris来修改头的注意力输出，作为prefix tuning。
• Scaled Parallel Adapter：通过将LoRA的组成和插入形式转移到适配器中的变体，如图3e所示。

6.2.5 MAM Adapters

作者对Adapter的放置和soft prompt进行了详细的调查。得出如下结论（详见论文实验部分）：

• 缩放并行适配器（Scaled parallel adapter ）是修改FFN的最佳变体。并行放置的Adapter优于顺序放置的Adapter，与 FFN 并行放置的Adapter优于与多头注意力（MHA）并行放置的Adapter（如下图中所示，蓝色表示修改Attention、红色表示修改FFN）。
• 当参数预算非常小的时候，修改head attention显示出最好的结果，而FFN在较大的容量下可以更好地利用修改。
• soft prompt（例如 prefix tuning）可以通过仅更改 0.1% 的参数来实现强大的性能。

图5：在XSum（左图）和en-ro（右图）上的结果。PA表示并行适配器。蓝色和红色标记分别在注意力和FFN子层应用修改

  基于此，作者提出了MAM（mix-and-match），最终模型 MAM Adapter 是用 FFN 层的并行Adapter和软提示的组合。具体而言，我们在注意力子层使用具有较小瓶颈维度（l=30）的前缀调整，并将更多的参数预算分配给使用缩放并行适配器（r=512）修改FFN表示。

  在表6中，我们将MAM适配器与各种参数高效调整方法进行了比较。为了完整起见，我们还在表6中展示了其他组合版本的结果：同时在注意力和FFN层使用并行适配器，并将前缀调整（attn）与LoRA（ffn）相结合——这两种组合版本都可以改进各自的原型

表6：各种参数高效调整方法及其提出的变种的比较。对于最高性能的方法，我们使用3个随机种子运行，并报告均值和标准差。

  通过上图实验结果，可以看到 MAM Adapter 在仅用了6.7%参数量（相比全量微调）的情况下，在Xsum和MT这两个任务上达到了和全量微调相近的效果，并且该方法大大优于 BitFit 和 Prompt Tuning，并始终优于 LoRA、Adapter 和 Prefix Tuning。

6.3 UniPELT（2021.10）

《UniPELT: A Unified Framework for Parameter-Efficient Language Model Tuning》

6.3.1 背景

  近年来，涌现出了许多针对语言模型的参数高效微调（PELT）方法，在模型训练参数极大的减少的情况下，模型效果与全量微调相当。但是不同的PELT方法在同一个任务上表现差异可能都非常大，这让针对特定任务选择合适的方法非常繁琐。

  基于此，作者提出了UniPELT方法，将不同的PELT方法作为子模块，并通过门控机制学习激活最适合当前数据或任务的方法。

6.3.2 模型结构

UniPELT是 LoRA、Prefix Tuning和Adapter的门控组合，其中：

• LoRA：通过低秩分解，将优化预训练参数$W_0$转换为优化外挂层$W_{down},W_{up}$的参数矩阵$W_B,W_A$；
• Prefix Tuning：在每个层的多头注意力中，在key和value的前面添加了l个可调节的前缀向量。具体来说，两组前缀向量$P^k,P^v\in {\mathbb{R}}^{l\times d}$与原始键K和值V进行连接。然后在新的前缀键和值上执行多头注意力计算。
• Adapter：在Transformer块的feed-forward子层之后添加Adapter模块

  然后组合这三个模块，每个模块使用门控机制（实现为线性层）来控制，即通过GP参数控制Prefix-tuning方法的开关，GL控制LoRA方法的开关，GA控制Adapter方法的开关。所有可训练参数（图中蓝颜色部分）包括 LoRA 的重参数化矩阵 $W_B,W_A$，提示调优参数$P_k,P_v$、Adapter参数和门函数权重。整个结构如下图所示：

6.3.3 实验

1. 低数据性能对比
   UniPELT 仅用 100 个示例就在低数据场景中展示了相对于单个 LoRA、Adapter 和 Prefix Tuning 方法的显著改进。在更高数据的场景中，UniPELT 的性能与这些方法相当或更好。

表格1：在GLUE基准测试中使用K = {100,500,1000}个训练样本的结果。评估指标为CoLA的Matthew’s相关性、MRPC和QQP的F1值、STS-B的Spearman’s相关性以及其余任务的准确率。对于MNLI，我们在匹配数据集上进行评估。我们报告了在五个随机种子上的平均性能，标准差作为下标。在每个设置下，最佳和次佳方法使用粗体和下划线标注。

2. 高数据对比
   • 表3列出了使用所有训练样本时，不同方法的性能，UniPELT整体上依旧是最佳的，但是优势没有低资源环境下那么高。这也是可以理解的，因为现有的PELT方法在充足的训练数据和改进潜力的情况下通常与全量精调性能相当。
   • 此外，仅仅组合多个PELT方法而不使用门控机制（UniPELT-NoGate），在高资源环境下效果不佳（平均比UniPELT低了0.89）。

表3：使用所有训练样本时在GLUE基准测试上的结果

3. 训练参数量、训练/推理时间对比
   • 训练参数量：LoRA，BitFit，Prefix-tuning都比较小，UniPELT参数量相对会多一些。
   • 训练速度：UniPELT比之前微调的方法多一些，但是还在能接受的范围，
   • 推理速度：BitFit方法增加的最少，UniPELT方法时间增加了27%。
     表格4：各种PEFT方法相对于fine-tuning的可训练参数数量和训练/推断时间对比

6.4 Compacter（略）

6.5 S4（略）

七 、RLHF（有空再补）

目前最好的端到端实现是微软的DeepSpeedChat。