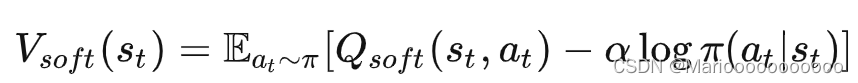算法SAC
- 基于动态规划的贝尔曼方城如下所示:
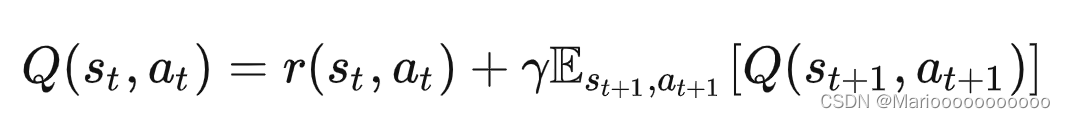
则,基于最大熵的软贝尔曼方程可以描述为如下的形式:
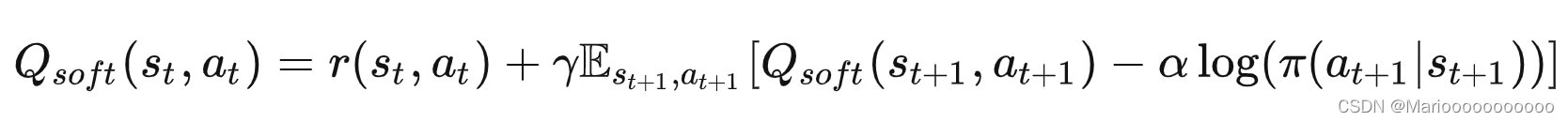
可以这么理解soft贝尔曼方程,就是在原有的贝尔曼方程的基础上添加了一个熵项。
另外一个角度理解soft-贝尔曼方程:
首先,将熵项作为奖励函数的一部分,写为如下的形式:
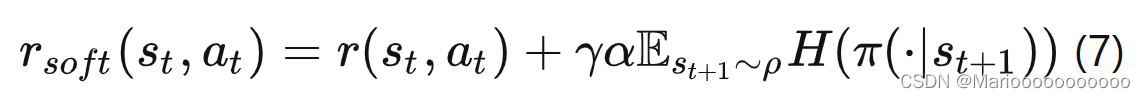
然后将这个 r s o f t r_{soft} rsoft带入到贝尔曼方程中去,然后通过进一步的转化形式,就可以得到可以得到如下的形式:
Q s o f t ( s t , a t ) = r ( s t , a t ) + γ α E s t + 1 ∼ ρ H ( π ( ⋅ ∣ s t + 1 ) ) + γ E s t + 1 , a t + 1 [ Q s o f t ( s t + 1 , a t + 1 ) ] = r ( s t , a t ) + γ E s t + 1 ∼ ρ , a t + 1 ∼ π [ Q s o f t ( s t + 1 , a t + 1 ) ] + γ α E s t + 1 ∼ ρ H ( π ( ⋅ ∣ s t + 1 ) = r ( s t , a t ) + γ E s t + 1 ∼ ρ , a t + 1 ∼ π [ Q s o f t ( s t + 1 , a t + 1 ) ] + γ E s t + 1 ∼ ρ E a t + 1 ∼ π [ − α log [ π ( a t + 1 ∣ s t + 1 ) ) = r ( s t , a t ) + γ E s t + 1 ∼ ρ [ E a t + 1 ∼ π [ Q s o f t ( s t + 1 , a t + 1 ) α log ( π ( a t + 1 ∣ s t + 1 ) ) ] ] = r ( s t , a t ) + γ E s t + 1 , a t + 1 [ Q s o f t ( s t + 1 , a t + 1 ) − α log [ π ( a t + 1 ∣ s t + 1 ) ) ] \begin{aligned} Q_{s o f t}\left(s_{t}, a_{t}\right) & =r\left(s_{t}, a_{t}\right)+\gamma \alpha \mathbb{E}_{s_{t+1} \sim \rho} H\left(\pi\left(\cdot \mid s_{t+1}\right)\right)+\gamma \mathbb{E}_{s_{t+1}, a_{t+1}}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right)\right] \\ & =r\left(s_{t}, a_{t}\right)+\gamma \mathbb{E}_{s_{t+1} \sim \rho, a_{t+1} \sim \pi}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right)\right]+\gamma \alpha \mathbb{E}_{s_{t+1} \sim \rho} H\left(\pi\left(\cdot \mid s_{t+1}\right)\right. \\ & =r\left(s_{t}, a_{t}\right)+\gamma \mathbb{E}_{s_{t+1} \sim \rho, a_{t+1} \sim \pi}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right)\right]+\gamma \mathbb{E}_{s_{t+1} \sim \rho} \mathbb{E}_{a_{t+1} \sim \pi}[-\alpha \operatorname{\log \left[\pi\left(a_{t+1} \mid s_{t+1}\right)\right)} \\ & =r\left(s_{t}, a_{t}\right)+\gamma \mathbb{E}_{s_{t+1} \sim \rho}\left[\mathbb{E}_{a_{t+1} \sim \pi}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right) \operatorname{\alpha } \log \left(\pi\left(a_{t+1} \mid s_{t+1}\right)\right)\right]\right] \\ & =r\left(s_{t}, a_{t}\right)+\gamma \mathbb{E}_{s_{t+1}, a_{t+1}}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right)-\alpha \log \left[\pi\left(a_{t+1} \mid s_{t+1}\right)\right)\right] \end{aligned} Qsoft(st,at)=r(st,at)+γαEst+1∼ρH(π(⋅∣st+1))+γEst+1,at+1[Qsoft(st+1,at+1)]=r(st,at)+γEst+1∼ρ,at+1∼π[Qsoft(st+1,at+1)]+γαEst+1∼ρH(π(⋅∣st+1)=r(st,at)+γEst+1∼ρ,at+1∼π[Qsoft(st+1,at+1)]+γEst+1∼ρEat+1∼π[−αlog[π(at+1∣st+1))=r(st,at)+γEst+1∼ρ[Eat+1∼π[Qsoft(st+1,at+1)αlog(π(at+1∣st+1))]]=r(st,at)+γEst+1,at+1[Qsoft(st+1,at+1)−αlog[π(at+1∣st+1))]
会得出同样的结论。
看上公式的最后一项,以及根据Q和v的关系函数:
Q
s
o
f
t
(
s
t
,
a
t
)
=
r
(
s
t
,
a
t
)
+
γ
E
s
t
+
1
,
a
t
+
1
[
Q
s
o
f
t
(
s
t
+
1
,
a
t
+
1
)
−
α
log
[
π
(
a
t
+
1
∣
s
t
+
1
)
)
]
\begin{aligned} Q_{s o f t}\left(s_{t}, a_{t}\right) & =r\left(s_{t}, a_{t}\right)+\gamma \mathbb{E}_{s_{t+1}, a_{t+1}}\left[Q_{s o f t}\left(s_{t+1}, a_{t+1}\right)-\alpha \log \left[\pi\left(a_{t+1} \mid s_{t+1}\right)\right)\right] \end{aligned}
Qsoft(st,at)=r(st,at)+γEst+1,at+1[Qsoft(st+1,at+1)−αlog[π(at+1∣st+1))]
Q
(
s
t
,
a
t
)
=
r
(
s
t
,
a
t
)
+
γ
E
s
t
+
1
∼
ρ
[
V
(
s
t
+
1
)
]
Q\left(s_t, a_t\right)=r\left(s_t, a_t\right)+\gamma \mathbb{E}_{s_{t+1} \sim \rho}\left[V\left(s_{t+1}\right)\right]
Q(st,at)=r(st,at)+γEst+1∼ρ[V(st+1)]
对比一下上面的这两个公式,也就是等号右侧应该是相等的,因此,软值函数形式为: