一、说明
信息熵是概率论在信息论的应用,它简洁完整,比统计方法更具有计算优势。在机器学习中经常用到信息熵概念,比如决策树、逻辑回归、EM算法等。本文初略介绍一个皮毛,更多细节等展开继续讨论。
二、关于信息熵的概念
2.1 要素描述
信息熵:熵是一种测量随机变量 X 的不确定性/随机性的方法。它有几个要素:
- 1)针对一个数据分布,现实中,是一组同母体的数据采样。
- 2)是对自身内部数据的不确定度量,这种度量是期望。
- 3)对于所有的分布,均匀分布不确定程度最大,没有更大的不确定性。
- 4)高斯分布不确定性程度最小,因为高斯分布有明确的核心,因此,很确定它就是一组μ附近的数据。
2.2 信息熵的数学表示:
1 连续概率分布:
2 离散概率分布
2.3 联合熵(Joint Entropy)
一对离散随机变量 X, Y ~ p (x, y) 的联合熵是指定它们的值平均所需的信息量。
联合熵是联合概率分布的不确定性或随机性的度量。它用于量化两个或多个随机变量一起包含的信息量。换句话说,联合熵是对由多个变量组成的系统中存在多少不确定性的度量。它通常用于信息论、通信理论和信号处理中,以评估信号或数据集中的信息量。在数学上,联合熵定义为所有可能结果的概率乘以它们的对数(以 2 为底)的负和。对于两个随机变量 X 和 Y,用 H(X,Y) 表示。
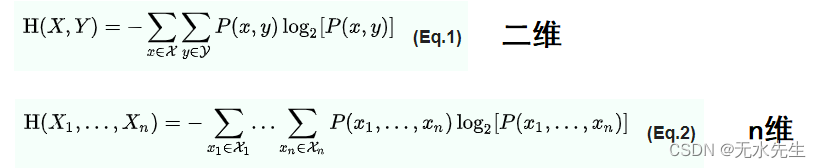
性质:
1)非负性:
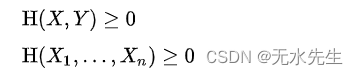
2)整体大于局部:(整体信息不确定程度大于局部)
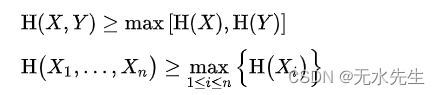
3)整体熵小于局部之和
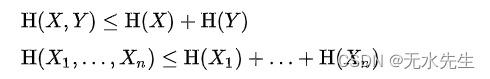
2.4 条件熵(Conditional Entropy)
条件熵:给定另一个 X 的随机变量 Y 的条件熵表示,在假定另一方知道 X 的情况下,一个人平均仍需要提供多少额外信息来传达 Y。
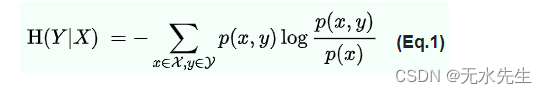
注意:条件熵也可以看成p(x,y)和p(x)的相对熵,也就是p(x,y)和p(x)的距离。
2.5 示例: 计算公平硬币的熵

这里,公平硬币的熵最大,即 1。随着硬币偏差的增加,信息/熵减少。下面是熵与偏差的关系图,曲线如下所示:

2.6 交叉熵:
交叉熵是给定随机变量或事件集的两个概率分布(p 和 q)之间差异的度量。换句话说,交叉熵是当我们使用模型 q 时对分布源 p 的数据进行编码所需的平均位数。
![]()
三、Kullback-Leibler 散度
3.1 KL散度定义
KL 散度是给定随机变量或事件集的两个概率分布之间的相对差异的度量。 KL 散度也称为相对熵。可以通过以下公式计算:
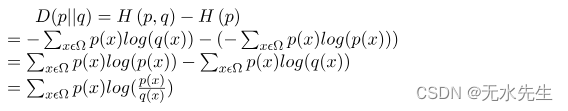
3.2 交叉熵和 KL 散度之间的区别
交叉熵计算表示分布 q 中的事件所需的总分布,而不是 p ,而 KL 散度表示表示分布中的事件所需的额外位数q 而不是 p。
3.3 KL 散度的性质
- D(p || q) 始终大于或等于 0。
- D(p || q) 不等于 D(q || p)。 KL 散度不具有交换性 。
- 如果 p=q,则 D(p || q) 为 0。
四、示例和实现
假设有两个盒子,里面装有 4 种类型的球(绿、蓝、红、黄)。从盒子中随机抽取一个具有给定概率的球。我们的任务是计算两个框的分布差异,即 KL 散度。
代码:解决这个问题的Python代码实现。
|
|
Output:
KL-divergence(box_1 || box_2): 0.057 KL-divergence(box_2 || box_1): 0.056 KL-divergence(box_1 || box_1): 0.000 Using Scipy rel_entr function KL-divergence(box_1 || box_2): 0.057 KL-divergence(box_2 || box_1): 0.056 KL-divergence(box_1 || box_1): 0.000
五、KL散度的应用:
熵和 KL 散度有许多有用的应用,特别是在数据科学和压缩方面。
熵可用于数据预处理步骤,例如特征选择。例如,如果我们想根据主题对不同的 NLP 文档进行分类,那么我们可以检查文档中出现的不同单词的随机性。 “计算机”一词出现在技术相关文档中的可能性更大,但“the”一词则不然。
熵还可以用于文本压缩和量化压缩。包含某种模式的数据比随机的数据更容易压缩。
KL 散度还用于许多 NLP 和计算机视觉模型(例如变分自动编码器)中,以比较原始图像分布和从编码分布生成的图像分布。