---

实验目的

1. 运用Python语言对多种格式数据进行读取；
2. 描述基于K均值模型的整个聚类过程；

---

实验内容

1. 使用Python语言读取事先标定的示例数据；
2. 从sklearn中导入K均值模型并对模型进行训练；
3. 对K均值模型进行分类性能评估和优化。

---

实验步骤

1、k均值聚类算法

1.1 k均值聚类算法的基本思想

       k均值聚类是基于样本集合划分的聚类算法。k均值聚类将样本集合划分为k个子集，构成k个类，将n个样本分到k个类中，每个样本到期所属类的中心的距离最小。每个样本只能属于一个类，所以k均值聚类是硬聚类。下面分别介绍k均值聚类的模型、策略、算法。
       k均值聚类的算法是一个迭代的过程，每一次迭代包括2个步骤。首先选择k个类的中心，将样本逐个指派到与其最近的中心的类中，得到一个聚类结果；然后更新每个类的样本的均值，作为类的新中新；重复以上步骤，直到收敛为止。

---

1.2 k均值聚类算法的聚类过程

k均值聚类算法的聚类过程主要包括以下几个步骤：
1、首先假设有k个聚类中心点，这些聚类中心点可以是从数据集随机选择的数据点。
2、对于一个给定的数据集，将每个数据点与距离其最近的聚类中心点相关联，从而将数据点分配给不同的聚类。
3、根据聚类中分配的数据点计算聚类中心点的平均值，并将该聚类中心点移动到该平均值处。
4、重复步骤2和3，直到聚类中心点不再变化，或达到预定的迭代次数。
5、最后，所有数据点将被分配到归属于它们所在的聚类中心点。

---

1.3 k均值聚类算法的算法叙述

输入：n个样本的集合X；
输出：样本集合的聚类C*。
具体实现过程：
1、初始化。令t=0，随机选择k个样本点作为初始聚类中心 。
2、对样本进行聚类。对固定的类中心，计算每个样本到类中心的距离，将每个样本指派到与其最近的中心的类中，构成聚类结果 。
3、计算新的类中心。对聚类结果 ，计算当前各个类中的样本的均值 。
4、如果迭代收敛或符合停止条件(中心点不再变化)，输出 ，否则，返回step(2)。

---

2、使用Python语言编写k均值聚类算法的源程序代码并分析其分类原理

---

2.1 读取文件数据并进行可视化

       使用pandas模块中的read_csv()函数读取"data.csv"文件，将数据集存储在一个DataFrame对象data中。
       通过调用drop()方法，删除data中的"labels"列，将特征值存储在X中，并将标签值存储在Y中。
       调用pd.value_counts()函数统计标签的种类及数量，并将结果输出到屏幕上。
       使用matplotlib模块中的pyplot子模块，绘制关于V1和V2的散点图。其中，plt.scatter()函数用于绘制散点图，plt.title()、plt.xlabel()和plt.ylabel()函数分别用于设置图表的标题、横坐标名称和纵坐标名称。最后通过plt.legend()函数添加图例，表明不同标签所代表的颜色。最后通过plt.show()函数显示图形。图1为将读取文件数据可视化后的结果：

---

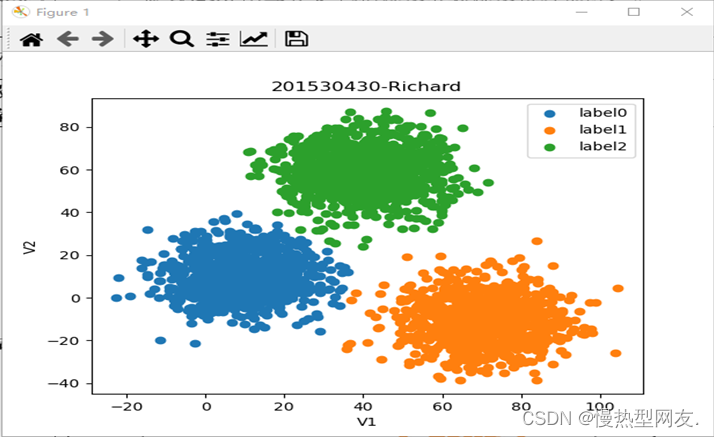
2.2 利用k均值算法对数据集进行聚类和可视化

       利用KMeans算法对数据集进行聚类，并对聚类结果进行可视化展示，具体步骤如下：
1、首先，使用sklearn.cluster模块中的KMeans类，创建一个KM对象。通过n_clusters参数指定聚类个数为3，通过random_state参数设置随机种子。
2、调用fit()方法，对数据集X进行聚类。
3、通过cluster_centers_属性获取聚类中心点的坐标，并将其存储在centers变量中。
4、通过matplotlib模块中的pyplot子模块，绘制关于V1和V2的散点图。
5、调用predict()方法，预测数据点所属的聚类标签，并用pd.value_counts()函数打印每个聚类的数据点数量。图2为聚类过程中的核心代码。

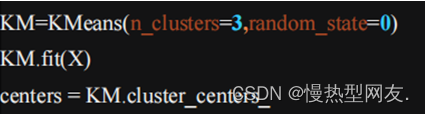
       这段代码主要是对数据集X进行了KMeans聚类操作，设置聚类数为3（即将数据划分为3个类别），并通过random_state参数设置了聚类初始化的随机数种子，保证每次运行程序时KMeans聚类结果的可重现性。

---

2.3 数据校正

2.3.1 第一次数据校正

       对数据进行了第一次校正，将 y_corrected 变量初始化为 y_predict，然后针对 y_corrected 中的值进行修改，使得簇的标签值发生变化。图3为第一次数据校正的代码。

       对聚类结果进行一次校正，将y_predict中标签为0和1的数据点的标签互换（因为原始数据集中标签0和1被反过来打上了标签）。图4为第一次数据校正结果。

---

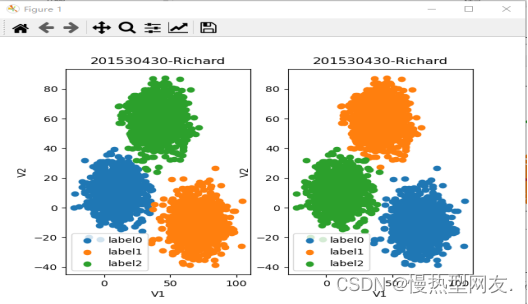
2.3.2 第二次数据校正

       使用pandas模块中的value_counts()函数，计算每个标签在y_corrected数组中的出现次数，并打印结果。
       将y_corrected转换为numpy数组类型，并使用sklearn.metrics模块中的accuracy_score()函数，计算真实标签Y和校正后的标签y_corrected之间的精度，并将结果存储在accuracy_corrected变量中。图4为第二次数据校正的代码。

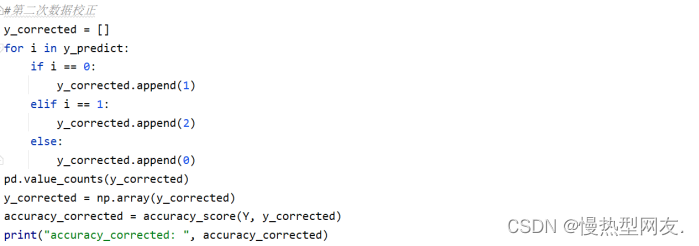
       对第一次聚类结果进行二次校正，将y_predict中标签为0、1和2的数据点的标签互换（因为原始数据集中标签0、1和2被反过来打上了标签）。图5为第二次数据校正的结果。

---

2.4 精度得分

       使用pandas模块中的value_counts()函数，计算每个标签在y_corrected数组中的出现次数，并打印结果。在上述两次数据校正过程中输出了两个数据，分别为accuracy_original，accuracy_corrected。图7为两个精度得分。

---

实验小结

       通过本次实验，我能够熟练叙述K均值聚类算法的基本思想；描述K均值聚类的整个聚类过程。可以根据实验内容完成使用Python语言编写K均值聚类的源程序代码并分析其分类原理。在实验过程中遇到了很多硬件或者是软件上的问题，请教老师，询问同学，上网查资料，都是解决这些问题的途径。最终将遇到的问题一一解决最终完成实验。
K均值聚类算法的优缺点：
优点：
1、属于无监督学习，无须准备训练集。
2、原理简单，实现起来较为容易。
3、结果可解释性较好。
缺点：
1、K 值需要预先给定，属于预先知识，很多情况下 K 值的估计是非常困难的，对于像计算全部微信用户的交往圈这样的场景就完全没有办法用 K-means 进行。此外，不合理的 k 值会使结果缺乏解释性。
2、K-means 算法对初始选取的聚类中心点比较敏感，不同的随机种子点得到的聚类结果完全不同；
3、该算法并不适合所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇，且对于异常点和离群点较为敏感；
4、易陷入局部最优解，在大规模数据集上收敛较慢。