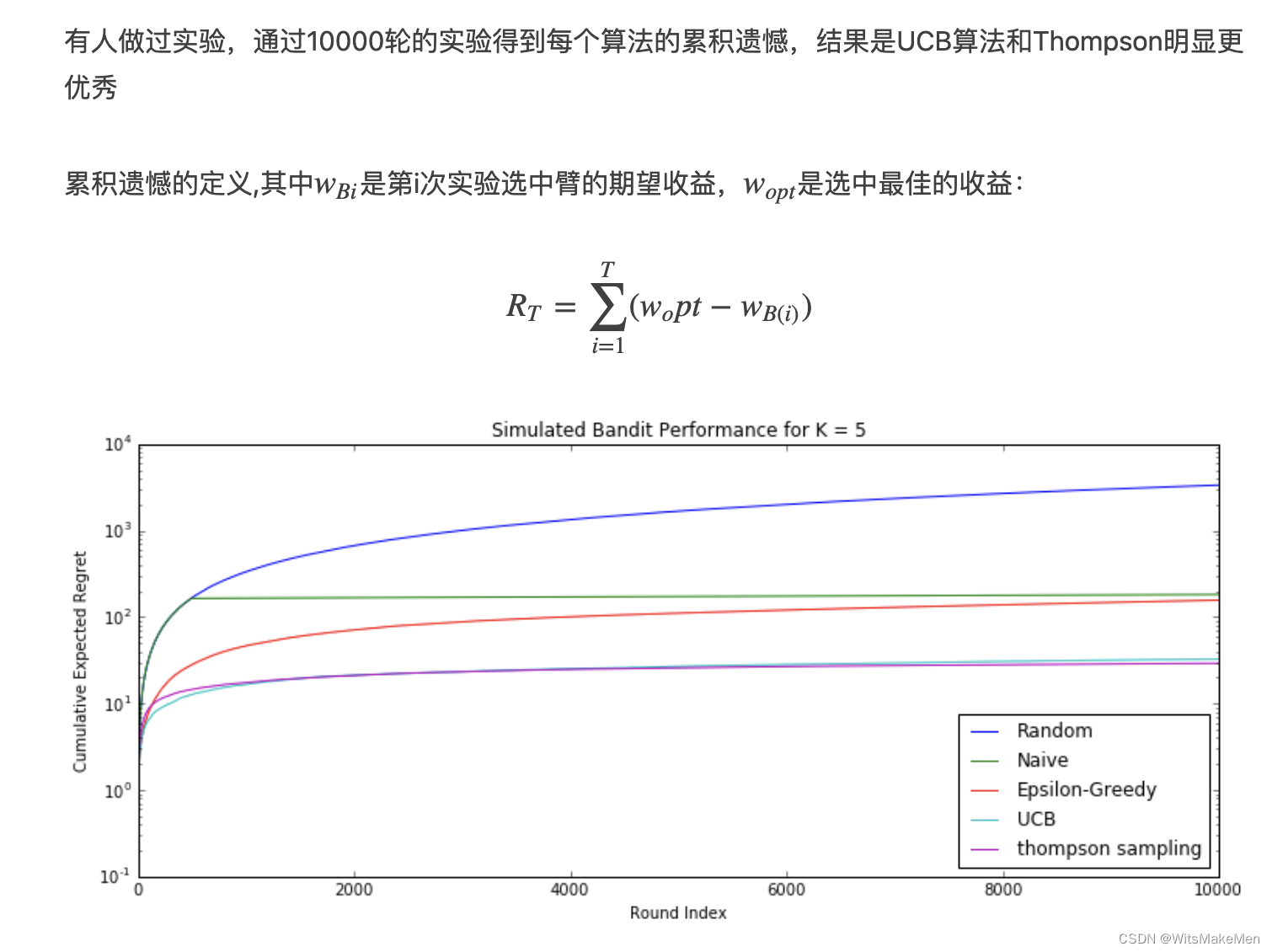
人生中有很多选择问题,当每天中午吃饭的时候,需要选择吃饭的餐馆,那么就面临一个选择,是选择熟悉的好吃的餐馆呢,还是冒风险选择一个没有尝试过的餐馆呢。同样的,推荐系统处处也面临着这样的选择,是推荐一个已经熟悉的点击率很高的物品呢,还是选择一个新的物品呢。这些都可以泛化成一个经典问题,多臂老虎机问题,也是一个研究很广的问题,这里介绍一些常用的bandit算法。
Topmpson sampling(汤普森采样)
假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为 p。
我们不断地试验,去估计出一个置信度较高的 “概率 p 的概率分布” 就能近似解决这个问题了。
怎么能估计 “概率 p 的概率分布” 呢? 答案是假设概率 p 的概率分布符合 beta(wins, lose)分布,它有两个参数: wins, lose。
每个臂都维护一个 beta 分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的 wins 增加 1,否则该臂的 lose 增加 1。
每次选择臂的方式是:用每个臂现有的 beta 分布产生一个随机数 b,选择所有臂产生的随机数中最大的那个臂去摇。
可以很简洁的用一行pyhton代码实现
import numpy as np
import pymc
N = 100
i = 0
win = [0 ,1, 3, 6, 10, 100]
trials = [0, 2, 5, 30, 21, 205]
while i<100:
choice = np.argmax(pymc.rbeta(1 + wins, 1 + trials - wins))
wins[choice] += 1
trials[choice] += 1
i += 1
这个算法中重要点的理解:

UCB算法(Upper Confidence Bound)

Epsilon-Greedy 算法

总结