前言
Gitee 代码地址:https://gitee.com/futurelqh/Multi-objective-evolutionary-optimization
理论分析
\quad\quad Srinivas 和 Deb 于 1993 年提出 了 NSGA (non-dominated sorting in genetic algorithm) (Srinivas et al, 1994)。NSGA 主要有三个方面的不足:一是没有最优个体 (elitist) 保留机制,有关研究表明(如文献Zitzler et al, 2000; Rudolph, 2001),最优个体保留机制一方面可以提高 MOEA 的性能,同时也能防止优秀解的丢失;二是共享参数问题,在进化过程中,主要是采用共享参数 σ s h a r e \sigma_{share} σshare 来维持解群体的分布性(基于共享机制的小生境技术),但共享参数的大小不容易确定, 参数的动态修改和调整更是一件困难的工作;三是构造 Pareto 最优解集(通常是构造进化群体的非支配集)的时间复杂度高,为 O ( r N 3 ) O(rN^3) O(rN3) (这里 r r r 为目标数, N N N 为进化群体的规模),因为每一代进化都需要构造非支配集,这样一来,当进化群体规模较大时,算法执行的时间开销就很大。为此,Deb 等于 2000 年在 NSGA 的基础上,提出了 NSGAII (Deb et al, 2000)。
\quad\quad 在 NSGA-II 中,将进化群体按支配关系分为若干层,第一层为进化群体的非支配个体集合,第二层为在进化群体中去掉第一层个体后所求得的非支配个体集合,第三层为在进化群体中去掉第一层和第二层个体后所求得的非支配个体集合,依此类推。选择操作首先考虑第一层非支配集,按照某种策略从第一层中选取个体;然后再考虑在第二层非支配个体集合中选择个体,依此类推,直至满足新进化群体的大小要求。
\quad\quad 下面从非支配集的构造方法、维持解集分布性的策略等方面进行比较详细的讨论。
\quad\quad 1. 非支配集的构造方法
\quad\quad 设群体 P o p Pop Pop 的规模大小为 N N N,将群体 P o p Pop Pop 按某种策略进行分类排序为 m m m 个子集 P 1 、 P 2 、 . . . 、 P m P_1、P_2、...、P_m P1、P2、...、Pm, 且满足下列性质:
\quad\quad ① ∪ p ∈ { P 1 , P 2 , . . . , P m } P = P o p \cup_{p \in \{P_1, P_2, ..., P_m\}} P = Pop ∪p∈{P1,P2,...,Pm}P=Pop (所有子集的并集为 P o p Pop Pop)
\quad\quad ② ∀ i , j ∈ { 1 , 2 , . . . , m } \forall i, j \in \{1, 2, ..., m\} ∀i,j∈{1,2,...,m} 且 i ≠ j , P i ∩ P j = ∅ i ≠ j,P_i \cap P_j = \emptyset i=j,Pi∩Pj=∅ (所有子集不存在相同的个体)
\quad\quad ③ P 1 ≻ P 1 ≻ ⋅ ⋅ ⋅ ≻ P m P_1 \succ P_1 \succ ··· \succ P_m P1≻P1≻⋅⋅⋅≻Pm,即 P k + 1 P_{k+1} Pk+1 中的个体直接受 P k P_k Pk 中个体的支配 ( k = 1 , 2 , . . . , m − 1 ) (k=1, 2, ..., m-1) (k=1,2,...,m−1)。
\quad\quad 对群体 P o p Pop Pop 进行分类排序的目的是为了将其划分成若干个满足上述三个性质的互不相交的子群体。对个体分类排序的依据为 P a r e t o Pareto Pareto 支配关系。
\quad\quad 设两个向量 { n p } \{n_p\} {np} 和 { s p } \{s_p\} {sp},其中 p ∈ P o p , n p p \in Pop,n_p p∈Pop,np 记录支配个体 p p p 的个体数, { s p } \{s_p\} {sp} 记录被个体 p p p 支配的个体的集合,即有
n p = ∣ { q ∣ q ≻ p p , q ∈ P o p } ∣ n_p = |\{q|q \succ p \quad p, q \in Pop\}| np=∣{q∣q≻pp,q∈Pop}∣
s p = ∣ { q ∣ p ≻ q p , q ∈ P o p } ∣ s_p = |\{q|p \succ q \quad p, q \in Pop\}| sp=∣{q∣p≻qp,q∈Pop}∣
\quad\quad 首先通过一个二重循环计算每个个体的 n p n_p np 和 s p s_p sp ,则 P 1 = { q ∣ n q = 0 , q ∈ P o p } P_1 = \{q~|~n_q = 0,q \in Pop\} P1={q ∣ nq=0,q∈Pop}。 然后依次按方法 P k = { 所 有 个 体 q ∣ n q − k + 1 = 0 } P_k = \{所有个体~ q~ | ~n_q - k + 1 = 0\} Pk={所有个体 q ∣ nq−k+1=0} 求 P 2 、 P 3 ⋅ ⋅ ⋅ P_2、P_3 ··· P2、P3⋅⋅⋅。
\quad\quad 构造分类子集的具体过程如算法 6.2 所示,其中, P 1 P_1 P1 为非支配集。

\quad\quad 算法 6.2 由两部分组成,第一部分用于计算 n i n_i ni 和 s i s_i si,并求得 P 1 P_1 P1, 所需要的时间为 ( r N 2 ) (rN^2) (rN2) ,这里 r r r 为目标数, N N N 为进化群体规模;第二部分用于求 P 2 、 P 3 、 ⋅ ⋅ ⋅ 、 P m P_2、P_3、···、P_m P2、P3、⋅⋅⋅、Pm, 最坏情况下一个规模为 N N N 的进化群体有 N N N 层边界集 (Pareto front),即 m = N m=N m=N , 此时其时间复杂度为 O ( N 2 ) O(N^2) O(N2)。由此可得,算法 6.2 的总时间复杂度为 O ( r N 2 ) 十 O ( N 2 ) O(rN^2)十O(N^2) O(rN2)十O(N2),即为 O ( r N 2 ) O(rN^2) O(rN2)。
\quad\quad Deb 等于 2002 年又提出了一种新的构造非支配集的方法 (Debet al, 2002),其时间复杂度仍为 O ( N 2 ) O(N^2) O(N2)
\quad\quad 2. 保持解群体分布性和多样性的方法
\quad\quad 为了保持解群体的分布性和多样性,Deb 等在文献 (Debet al, 2000) 中,首先通过计算进化群体中每个个体的聚集距离,然后依据个体所处的层次及其聚集距离,定义一个偏序集 (partial order set),构造新群体时依次在偏序集中选择个体。
\quad\quad 在产生新群体时,通常将优秀且 聚集密度 比较小的个体保留并参与下一代进化。聚集密度小的个体其聚集距离反而大,一个个体的聚集距离可以通过计算与其相邻的两个个体在每个子目标上的距离差之和来求取。如图 6.6 所示,设有两个子目标 f 1 f_1 f1 和 f 2 f_2 f2,个体 i i i 的聚集距离是图中虚线四边形的长与宽之和。设 P [ i ] d i s t a n c e P[i]_{distance} P[i]distance 为个体 i i i 的聚集距离, P [ i ] . m P[i].m P[i].m 为个体 i i i 在子目标 m m m 上的函数值,则图 6.6 中个体 i i i 的聚集距离为
P [ i ] d i s t a n c e = ( P [ i + 1 ] . f 1 − P [ i − 1 ] . f 1 ) + ( P [ i + 1 ] . f 2 − P [ i − 1 ] . f 2 ) P[i]_{distance} = (P[i + 1].f_1 - P[i-1].f_1) + (P[i + 1].f_2 - P[i-1].f_2) P[i]distance=(P[i+1].f1−P[i−1].f1)+(P[i+1].f2−P[i−1].f2)

\quad\quad 一般情况下,当有 r r r 个子目标时个体 i i i 的聚集距离为
P [ i ] d i s t a n c e = ∑ k = 1 r ( P [ i + 1 ] . f k − P [ i − 1 ] . f k ) P[i]_{distance} = \sum_{k=1}^{r}( P[i + 1].f_k - P[i-1].f_k) P[i]distance=k=1∑r(P[i+1].fk−P[i−1].fk)
\quad\quad 为了计算每个个体的聚集距离,需要对群体 P P P 按每个子目标函数值进行排序,当釆用最好的排序方法时(如快速排序、堆排序等),若群体规模为 N N N,最坏情况下对 r r r 个子目标分别进行排序的时间复杂度为 O ( r N l o g N ) O(rNlogN) O(rNlogN)
\quad\quad 计算个体聚集距离的方法如算法 6.3 所示(TamakietaL 1995)

\quad\quad 算法 6.3 在最坏情况下对 r r r 个子目标分别进行排序的时间为 O ( r N l o g N ) O(rNlogN) O(rNlogN),计算每个个体的聚集距离的时间为 O ( r N ) , O(rN), O(rN), 因此算法的时间复杂度为 O ( r N l o g N ) O(rNlogN) O(rNlogN)。
\quad\quad 3. Deb 的 NSGA-II
\quad\quad 在具体讨论 NSGA-II 之前,先讨论建立在进化群体上的一类偏序关系,因为 NSGA-II 在构造新群体时,将依据这种偏序关系进行选择操作。定义进化群体的偏序关系时,主要考虑下列两个因素:
\quad\quad ① 个体 i i i 的分类序号 i r a n k , i r a n k = k i_{rank},i_{rank}=k irank,irank=k 当且仅当 i ∈ P k i \in P_k i∈Pk \quad (根据支配关系给每个个体编号: i r a n k i_{rank} irank = 支配 i i i 的个体数 + 1, i ∈ P k i \in P_k i∈Pk:表示 i i i 是属于第 k 层非支配集)
\quad\quad ② 个体 i i i 的聚集距离 P [ i ] d i s t a n c e P[i]_{distance} P[i]distance \quad\quad 详细介绍见 3.2
\quad\quad 得到偏序关系的定义如下。
\quad\quad 定义 6.1 \quad 设个体 i i i 和 j j j 为进化群体中的任意个体,个体之间的偏序(partial order) 关系 ≻ n \succ_n ≻n 为
i ≻ n j i f ( i r a n k < j r a n k ) o r ( i r a n k = j r a n k ) a n d ( P [ i ] d i s t a n c e > P [ j ] d i s t a n c e ) i \succ_n j \quad if(i_{rank} < j_{rank})~ or~ (i_{rank} = j_{rank}) ~and~ (P[i]_{distance} > P[j]_{distance}) i≻njif(irank<jrank) or (irank=jrank) and (P[i]distance>P[j]distance)
\quad\quad 定义 6.1 表明,当两个个体属于不同的分类排序子集时,优先考虑序号 i r a n k i_{rank} irank 小的个体; 当序号 i r a n k i_{rank} irank 相同时,则优先考虑聚集距离大或者说聚集密度小的个体。 聚集距离,聚集密度详细介绍见 3.
\quad\quad 在 NSGA-II 中,开始时随机产生一个初始群体 P 0 P_0 P0,在此基础上采用二元锦标赛选择 (binary tournament selection) 、交叉(crossover)和变异操作(mutation) 产生一个新群体 Q 0 Q_0 Q0, P 0 P_0 P0 和 Q 0 Q_0 Q0 的群体规模均为 N N N。将 P t P_t Pt 和 Q t Q_t Qt 并入到 R t R_t Rt 中(初始时 t = 0 t = 0 t=0),对 R t R_t Rt 进行分类排序,然后根据需要计算某个分类排序子集中所有个体的聚集距离,并按照定义 6.1 建立偏序集。接下来从偏序集依次选取个体进入 P t + 1 P_{t+1} Pt+1,直至 P t + 1 P_{t+1} Pt+1 的规模为 N N N。具体过程如算法 6.4 所示。

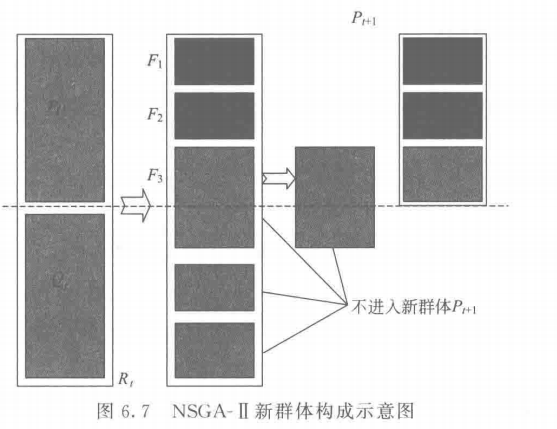
\quad\quad 算法 6.4 中,通过 F = nondominated-sort( R t R_t Rt) 产生了若干个分类子集 F = ( F 1 , F 2 , ⋅ ⋅ ⋅ ) F=(F_1, F_2, ···) F=(F1,F2,⋅⋅⋅),但被选入新群体的只有一部分。如图 6.7 所示,分类子集 F 1 F_1 F1 和 F 2 F_2 F2 中的所有个体均被选入了新群体 P t + 1 P_{t +1} Pt+1,但分类子集 F 3 F_3 F3 中只有一部分个体被选入新群体 P t + 1 P_{t + 1} Pt+1。 一般地,若 ∣ F 1 ∣ + ∣ F 2 ∣ + ⋅ ⋅ ⋅ + ∣ F i − 1 ∣ ≤ N |F_1| + |F_2| + ··· + |F_{i-1}| ≤ N ∣F1∣+∣F2∣+⋅⋅⋅+∣Fi−1∣≤N 且 ∣ F 1 ∣ + ∣ F 2 ∣ + ⋅ ⋅ ⋅ + ∣ F i ∣ > N |F_1| + |F_2| + ··· + |F_{i}| > N ∣F1∣+∣F2∣+⋅⋅⋅+∣Fi∣>N,则称 F i F_i Fi 为临界层分类子集,图 6.7 中的 F 3 F_3 F3 为临界层分类子集。
\quad\quad 算法 6-4 的时间开销主要由三部分组成(其中 r r r 为目标数):
\quad\quad ① 构造分类子集(non-dominated sort) : O ( r ( 2 N ) 2 ) O(r(2N)^2) O(r(2N)2)。
\quad\quad ② 计算聚集距离(crowding distance assignment): O ( r ( 2 N ) l o g ( 2 N ) ) O(r(2N )log(2N)) O(r(2N)log(2N))。
\quad\quad ③ 构造偏序集(sorting on >〃): O ( 2 N I o g ( 2 N ) ) O(2NIog(2N)) O(2NIog(2N))。
\quad\quad 由此可得算法 6.4 的总时间复杂度为 O ( r N 2 ) O(rN^2) O(rN2),其中主要的时间开销花费在构造边界集上,因此一个快速的构造分类子集(或构造非支配集)的方法有利于提高 MOEA 的效率。
算法运行效果
当选用 DTLZ1 作为测试函数,目标数设置为 3 时

代码实现
main.m
function main()
% UserInput.Probleme = problem;
% UserInput.ObjectNum = dimension;
[UserInput] = GetUserInput()
switch (UserInput.Probleme)
case 1
AlgoName = 'DTLZ1';
case 2
AlgoName = 'DTLZ2';
case 3
AlgoName = 'DTLZ3';
case 4
AlgoName = 'DTLZ4';
end
NSGAII(AlgoName, UserInput.ObjectNum);
end
NSGAII.m
function NSGAII(Problem,M)
% Function: NSGAII(Problem,M)
%
% Description: 执行 NSGAII 算法的所有逻辑
%
%
% Syntax:
%
%
% Parameters:
% Problem:选择测试函数,例如:'DTLZ1',注意输出字符
% M : 目标函数个数
%
% Return:
% 无
%
% Young99
% Revision:1.0 Data: 2022-12-06
%*************************************************************************
clc;
format compact;% 空格紧凑
tic; % 记录运行时间
% 参数设定
Generations = 700; % 迭代次数
if M == 2 % 目标数量
N = 100; % 种群大小
else M == 3
N = 105;
end
% 初始化种群,返回初始化种群和决策变量上下限
[Population,Boundary] = Objective(0, Problem, M, N);
FunctionValue = Objective(1,Problem,M,Population);% 计算目标函数值
% 进行非支配排序
FrontValue = NonDominateSort(FunctionValue,0);
CrowdDistance = CrowdDistances(FunctionValue,FrontValue); % 计算聚集距离
%开始迭代
for Gene = 1 : Generations
%产生子代。
MatingPool = Mating(Population,FrontValue,CrowdDistance); % 交配池选择。2 的锦标赛选择方式
Offspring = NSGA_Gen(MatingPool,Boundary,N); % 交叉,变异,越界处理并生成新的种群
%% 精英保留策略
Population = [Population; Offspring]; % 种群合并
FunctionValue = Objective(1,Problem,M,Population); % 计算目标函数值
[FrontValue,MaxFront] = NonDominateSort(FunctionValue,1); % 进行非支配排序
CrowdDistance = CrowdDistances(FunctionValue,FrontValue); % 计算聚集距离
% 选出非支配的个体
Next = zeros(1,N);
NoN = numel(FrontValue,FrontValue<MaxFront);
Next(1:NoN) = find(FrontValue<MaxFront);
% 选出最后一个面的个体
Last = find(FrontValue==MaxFront);
[~,Rank] = sort(CrowdDistance(Last),'descend');
Next(NoN+1:N) = Last(Rank(1:N-NoN));
% 下一代种群
Population = Population(Next,:);
FrontValue = FrontValue(Next);
CrowdDistance = CrowdDistance(Next);
FunctionValue = Objective(1,Problem,M,Population);
cla;%cla 从当前坐标区删除包含可见句柄的所有图形对象
%绘图
for i = 1 : MaxFront
FrontCurrent = find(FrontValue==i);
DrawGraph(FunctionValue(FrontCurrent,:));
hold on;
switch Problem %
case 'DTLZ1'
if M == 2
pareto_x = linspace(0,0.5);
pareto_y = 0.5 - pareto_x;
plot(pareto_x, pareto_y, 'r');
elseif M == 3
[pareto_x,pareto_y] = meshgrid(linspace(0,0.5));
pareto_z = 0.5 - pareto_x - pareto_y;
axis([0,1,0,1,0,1]);
mesh(pareto_x, pareto_y, pareto_z);
end
otherwise
if M == 2
pareto_x = linspace(0,1);
pareto_y = sqrt(1-pareto_x.^2);
plot(pareto_x, pareto_y, 'r');
elseif M == 3
[pareto_x,pareto_y,pareto_z] =sphere(50);
axis([0,1,0,1,0,1]);
mesh(1*pareto_x,1*pareto_y,1*pareto_z);
end
end
pause(0.01);
end
clc;
end
end
Objective.m:进行种群初始化

function [Output,Boundary] = Objective(Operation,Problem,M,Input)
% Function: [Output,Boundary] = Objective(Operation,Problem,M,Input)
%
% Description: Initial population and compute objective function value
%
%
% Syntax:
%
%
% Parameters:
% Operation: if Operation is 0, Initial population. if Operation is 1,
% comput funcitn value
% Problem:Test function name. such as 'DTLZ1'
% M: function numbers
% Input: Population numbers
%
% Return:
% Output: if Operation is 0, Output is Initial result, Operation is 1,
% Output is functionvalue
%
% Boundary: function boundary
%
% Young99
% Revision: 1.0 Data: 2022-12-06
%*************************************************************************
% input:N 种群规模
persistent K; % 定义持久变量
% 持久变量是声明它们的函数的局部变量;
% 但其值保留在对该函数的各次调用所使用的内存中。
Boundary = NaN;
switch Operation % 选择操作模式 0/1
% 0:初始化种群
case 0
k = find(~isstrprop(Problem,'digit'),1,'last'); % 判断输入的 Problem 有几个英文字母
%“~” 对0/1数组取反
K = [5 10 10 10 10];
K = K(str2double(Problem(k+1:end))); %'DTZL2'K=10
%str2double是一种函数,其功能是把字符串转换数值,
D = M + K-1; % D:变量数量, M:目标函数个数 K: K = D - M + 1
MaxValue = ones(1,D);
MinValue = zeros(1,D);
Population = rand(Input,D); % 确定种群大小:( N * D)
Population = Population.*repmat(MaxValue,Input,1)+(1-Population).*repmat(MinValue, Input, 1);
% 产生新的初始种群
Output = Population;
Boundary = [MaxValue;MinValue];
% 1:计算目标函数值;这里只包含 DTLZ1~DTZL4 函数问题
case 1
Population = Input; % 已经初始化完成的种群
FunctionValue = zeros(size(Population,1),M);
switch Problem
case 'DTLZ1'
g = 100*(K+sum((Population(:,M:end)-0.5).^2-cos(20.*pi.*(Population(:,M:end)-0.5)),2));
for i = 1 : M % 计算第 i 维目标函数值
FunctionValue(:,i) = 0.5.*prod(Population(:,1:M-i),2).*(1+g);
if i > 1
FunctionValue(:,i) = FunctionValue(:,i).*(1-Population(:,M-i+1));
end
end
case 'DTLZ2'
g = sum((Population(:,M:end)-0.5).^2,2);
for i = 1 : M
FunctionValue(:,i) = (1+g).*prod(cos(0.5.*pi.*Population(:,1:M-i)),2);
if i > 1
FunctionValue(:,i) = FunctionValue(:,i).*sin(0.5.*pi.*Population(:,M-i+1));
end
end
case 'DTLZ3'
g = 100*(K+sum((Population(:,M:end)-0.5).^2-cos(20.*pi.*(Population(:,M:end)-0.5)),2));
for i = 1 : M
FunctionValue(:,i) = (1+g).*prod(cos(0.5.*pi.*Population(:,1:M-i)),2);
if i > 1
FunctionValue(:,i) = FunctionValue(:,i).*sin(0.5.*pi.*Population(:,M-i+1));
end
end
case 'DTLZ4'
Population(:,1:M-1) = Population(:,1:M-1).^100;
g = sum((Population(:,M:end)-0.5).^2,2);
for i = 1 : M
FunctionValue(:,i) = (1+g).*prod(cos(0.5.*pi.*Population(:,1:M-i)),2);
if i > 1
FunctionValue(:,i) = FunctionValue(:,i).*sin(0.5.*pi.*Population(:,M-i+1));
end
end
case 'DTLZ5'
g = sum((Population(:,M:end)-0.5).^2,2);
for i = 1 : M
theta =(pi./(4*(1+g))).*(1+2.*g.*Population(:,1:M-i));
FunctionValue(:,i) = (1+g).*prod(cos(0.5.*pi.*theta),2);
if i > 1
FunctionValue(:,i) = FunctionValue(:,i).*sin(0.5.*pi.*(pi./(4*(1+g))).*(1+2.*g.*Population(:,M-i+1)));
end
end
end
Output = FunctionValue;
end
end
NonDominateSort.m:构造非支配集
function [FrontValue,MaxFront] = NonDominateSort(FunctionValue,Operation)
% Function: [FrontValue,MaxFront] = NonDominateSort(FunctionValue,Operation)
%
% Description: 进行非支配排序
%
%
% Syntax:
%
%
% Parameters:
% FunctionValue, 待排序的种群(目标空间),的目标函数值
% Operation, 可指定仅排序第一个面,排序前一半个体,或是排序所有的个体, 默认为排序所有的个体
%
% Return:
% FrontValue, 排序后的每个个体所在的前沿面编号, 未排序的个体前沿面编号为inf
% MaxFront, 排序的最大前面编号
%
%
% Young99
% Revision: 1.0 Data: 2022-12-06
%*************************************************************************
if Operation == 1
Kind = 2;
else
Kind = 1;
end
[N,M] = size(FunctionValue);
MaxFront = 0;
cz = zeros(1,N); %% 记录个体是否已被分配编号
FrontValue = zeros(1,N)+inf; % 每个个体的前沿面编号初始化为无穷:inf
[FunctionValue,Rank] = sortrows(FunctionValue);
% sortrows:由小到大以某行的方式进行排序(默认为第一行),返回排序结果和检索到的数据(按相关度排序)在原始数据中的索引
%开始迭代判断每个个体的前沿面,采用改进的 deductive sort,Deb 非支配排序算法
% 代码思路:最外层的 while 表示,
% 当 kind = 1,,且所有个体均编号了,退出循环,
% 或 kind = 2,一般个体已经被选出编号了
% 或 kind = 3,并且只选出第一层非支配集
% while 内嵌套了三层 for 循环,最外层 for 循环固定一个个体,
% 内层 for 循环将后面其他所有个体与此个体进行两两比较,将被次个体支配的个体标号 d(j) = 1,
% 在后面循环中直接跳过(~d(i)),下次进入 if 语句的第一个个体,即为与个体 i 同层级的个体(与 i 是非支配关系)
% 从而在 for 遍历完所有个体后,可选出当前层级的所有个体,并执行 d = cz,在后续筛选个体时,跳过上一次已经筛选出的个体
% MaxFront 用于对当前层级的个体进行编号,即第一轮为支配集 P1,第二轮个体为 P2
while (Kind==1 && sum(cz)<N) || (Kind==2 && sum(cz)<N/2) || (Kind==3 && MaxFront<1)
MaxFront = MaxFront + 1;
d = cz;
% 最外层两个 for 循环用于个体之间两两比较,最内层的 for 循环用于,选出的两个个体进行每个函数值的比较
for i = 1 : N
if ~d(i)
for j = i + 1 : N
if ~d(j)
k = 1; % 作为标记
for m = 2 : M
if FunctionValue(i,m) > FunctionValue(j,m) %比较函数值,判断个体的支配关系
k = 0;
break;
end
end
if k == 1
d(j) = 1; % 将所有被 i 支配的都标记为 1
end
end
end
FrontValue(Rank(i)) = MaxFront;
cz(i) = 1; % 将当前的个体标记为 1,表示已经确定所在的非支配层级
end
end
end
end
%% 非支配排序伪代码
% def fast_nondominated_sort( P ):
% F = [ ]
% for p in P:
% Sp = [ ] #记录被个体p支配的个体
% np = 0 #支配个体p的个数
% for q in P:
% if p > q: #如果p支配q,把q添加到Sp列表中
% Sp.append( q ) #被个体p支配的个体
% else if p < q: #如果p被q支配,则把np加1
% np += 1 #支配个体p的个数
% if np == 0:
% p_rank = 1 #如果该个体的np为0,则该个体为Pareto第一级
% F1.append( p )
% F.append( F1 )
% i = 0
% while F[i]:
% Q = [ ]
% for p in F[i]:
% for q in Sp: #对所有在Sp集合中的个体进行排序
% nq -= 1
% if nq == 0: #如果该个体的支配个数为0,则该个体是非支配个体
% q_rank = i+2 #该个体Pareto级别为当前最高级别加1。此时i初始值为0,所以要加2
% Q.append( q )
% F.append( Q )
% i += 1
CrowdDistances.m:计算拥挤距离

function CrowdDistance = CrowdDistances(FunctionValue,FrontValue)
% Function: CrowdDistance = CrowdDistances(FunctionValue,FrontValue)
%
% Description: 分前沿面计算种群中每个个体的拥挤距离
%
%
% Syntax:
%
%
% Parameters:
% FunctionValue:每个个体的目标函数值
% FrontValue:每个个体的最大前沿面编号
%
% Return:
% CrowdDistance:每个个体的拥挤距离
%
% Young99
% Revision: Data:
%*************************************************************************
[N,M] = size(FunctionValue);
CrowdDistance = zeros(1,N);
Fronts = setdiff(unique(FrontValue),inf);
for f = 1 : length(Fronts)
Front = find(FrontValue==Fronts(f));
Fmax = max(FunctionValue(Front,:),[],1);
Fmin = min(FunctionValue(Front,:),[],1);
for i = 1 : M
[~,Rank] = sortrows(FunctionValue(Front,i));
CrowdDistance(Front(Rank(1))) = inf;
CrowdDistance(Front(Rank(end))) = inf;
for j = 2 : length(Front)-1
CrowdDistance(Front(Rank(j))) = CrowdDistance(Front(Rank(j)))+(FunctionValue(Front(Rank(j+1)),i)-FunctionValue(Front(Rank(j-1)),i))...
/(Fmax(i)-Fmin(i)); % 除以最大值 - 最小值,即对其标准化处理
end
end
end
end
Mating.m:二元锦标赛选择个体
function MatingPool = Mating(Population,FrontValue,CrowdDistance)
% Function:MatingPool = Mating(Population,FrontValue,CrowdDistance)
%
% Description: 通过二元锦标赛选择方式,选择后代个体
% 模拟自然界中一个普遍存在的规律,即优秀个体有更大的概率能够繁衍后代。
%
% Syntax:
%
%
% Parameters:
% Population:种群
% FrontValue:每个种群对应的最大前沿面
% CrowdDistance:每个种群的拥挤距离
%
% Return:
% MatingPool:经过交配池留下的种群
%
% Young99
% Revision:1.0 Data: 2022-12-06
%*************************************************************************
[N,D] = size(Population);
% 二元联赛选择
MatingPool = zeros(N,D);
Rank = randperm(N); % randperm 将一列序号随机打乱,序号必须是整数
Pointer = 1;
for i = 1 : 2 : N
%选择父母
k = zeros(1,2);
for j = 1 : 2
if Pointer >= N
Rank = randperm(N);
Pointer = 1;
end
p = Rank(Pointer);
q = Rank(Pointer+1); % 规模为2的锦标赛选择方式
if FrontValue(p) < FrontValue(q)
k(j) = p;
elseif FrontValue(p) > FrontValue(q)
k(j) = q;
elseif CrowdDistance(p) > CrowdDistance(q)
k(j) = p;
else
k(j) = q;
end
Pointer = Pointer + 2;
end
MatingPool(i,:) = Population(k(1),:);
MatingPool(i+1,:) = Population(k(2),:);
end
end
NSGA_Gen.m:模拟二进制交叉、多项式变异
function Offspring = NSGA_Gen(MatingPool,Boundary,MaxOffspring)
% Function: Offspring = NSGA_Gen(MatingPool,Boundary,MaxOffspring)
%
% Description: 通过遗传算法利用模拟二进制交叉,多项式变异生成新的种群
%
%
% Syntax:
%
%
% Parameters:
% MatingPool, 交配池, 其中每第 i 个和第 i+1 个个体交叉产生两个子代, i 为奇数
% Boundary, 决策空间, 其第一行为空间中每维的上界, 第二行为下界
% MaxOffspring, 返回的子代数目, 若缺省则返回所有产生的子代, 即和交配池的大小相同
%
% Return:
% Offspring, 产生的子代新种群
%
% Young99
% Revision: Data:
%*************************************************************************
[N,D] = size(MatingPool);
if nargin < 3 || MaxOffspring < 1 || MaxOffspring > N
MaxOffspring = N;
end
% 遗传操作参数
ProC = 1; % 交叉概率
ProM = 1/D; % 变异概率
DisC = 20; % 交叉参数
DisM = 20; % 变异参数
% 模拟二进制交叉
Offspring = zeros(N,D);
for i = 1 : 2 : N
beta = zeros(1,D);
miu = rand(1,D);
beta(miu<=0.5) = (2*miu(miu<=0.5)).^(1/(DisC+1));
beta(miu>0.5) = (2-2*miu(miu>0.5)).^(-1/(DisC+1));
beta = beta.*(-1).^randi([0,1],1,D);
beta(rand(1,D)>ProC) = 1;
Offspring(i,:) = (MatingPool(i,:)+MatingPool(i+1,:))/2+beta.*(MatingPool(i,:)-MatingPool(i+1,:))/2;
Offspring(i+1,:) = (MatingPool(i,:)+MatingPool(i+1,:))/2-beta.*(MatingPool(i,:)-MatingPool(i+1,:))/2;
end
Offspring = Offspring(1:MaxOffspring,:); % 用于选取自带个体数 MaxOffspring
% 多项式变异
if MaxOffspring == 1
MaxValue = Boundary(1,:);
MinValue = Boundary(2,:);
else
MaxValue = repmat(Boundary(1,:),MaxOffspring,1);
MinValue = repmat(Boundary(2,:),MaxOffspring,1);
end
k = rand(MaxOffspring,D); % 随机选定要变异的基因位
miu = rand(MaxOffspring,D); % 采用多项式变异
Temp = k<=ProM & miu<0.5; % 要变异的基因位
Offspring(Temp) = Offspring(Temp)+(MaxValue(Temp)-MinValue(Temp)).*((2.*miu(Temp)+(1-2.*miu(Temp)).*(1-(Offspring(Temp)-MinValue(Temp))./(MaxValue(Temp)-MinValue(Temp))).^(DisM+1)).^(1/(DisM+1))-1);
Temp = k<=ProM & miu>=0.5;
Offspring(Temp) = Offspring(Temp)+(MaxValue(Temp)-MinValue(Temp)).*(1-(2.*(1-miu(Temp))+2.*(miu(Temp)-0.5).*(1-(MaxValue(Temp)-Offspring(Temp))./(MaxValue(Temp)-MinValue(Temp))).^(DisM+1)).^(1/(DisM+1)));
%越界处理
Offspring(Offspring>MaxValue) = MaxValue(Offspring>MaxValue); %子代越上界处理
Offspring(Offspring<MinValue) = MinValue(Offspring<MinValue); %子代越下界处理
end
DrawGraph.m:绘图
function Handle = DrawGraph(FigureData,FigureFormat)
% Function:Handle = DrawGraph(FigureData,FigureFormat)
%
% Description: 绘制出指定数据的图形
%
%
% Syntax:
%
%
% Parameters:
% FigureData, 待绘制的数据矩阵(即点的坐标集合)
% FigureFormat, 图形的格式, 可省略
%
% Return:
% Handle, 图形的句柄
%
% Young99
% Revision: 1.0 Data: 2022-12-06
%*************************************************************************
A = 1;
switch size(FigureData,2)
case 2
hold on;box on
set(gca, 'Fontname', 'Times New Roman', 'Fontsize', 13)
if nargin < 2 || ~ischar(FigureFormat)
Handle = plot(FigureData(:,1),FigureData(:,2),'ok','MarkerSize',6,'Marker','o','Markerfacecolor',[0 0 0]+0.4,'Markeredgecolor',[0 0 0]+0.7);
else
Handle = plot(FigureData(:,1),FigureData(:,2),FigureFormat);
end
axis tight
xlabel('f_1')
ylabel('f_2')
case 3
hold on;box on
set(gca, 'Fontname', 'Times New Roman', 'Fontsize', 13)
if nargin < 2 || ~ischar(FigureFormat)
Handle = plot3(FigureData(:,1),FigureData(:,2),FigureData(:,3),'ok','MarkerSize',8,'Marker','o','Markerfacecolor',[0 0 0]+0.4,'Markeredgecolor',[0 0 0]+0.7);
else
Handle = plot3(FigureData(:,1),FigureData(:,2),FigureData(:,3),FigureFormat);
end
axis tight
xlabel('f_1')
ylabel('f_2')
zlabel('f_3')
view(135,30)
otherwise
hold on;box on;
if A == 1
Num = size(FigureData,1);
for i = 1 : Num
plot(FigureData(i,:),'bo-');
end
Handle = NaN;
elseif A == 2
M = size(FigureData,2);
SumM = sum([1:M-1]);
RowValue = floor(sqrt(SumM));
while mod(SumM,RowValue) ~= 0
RowValue = RowValue - 1;
end
LineValue = SumM / RowValue;
Num = 1;
for i = 1 : M
for j= i+1 : M
subplot(RowValue,LineValue,Num);
plot(FigureData(:,i),FigureData(:,j),'b*');
Num = Num + 1;
end
end
Handle = NaN;
end
end
end





![[附源码]Python计算机毕业设计Django校园帮平台管理系统](https://img-blog.csdnimg.cn/2f83f9c90409425daffdf885597f9685.png)

![[附源码]计算机毕业设计面向高校活动聚AppSpringboot程序](https://img-blog.csdnimg.cn/b77492b393d94f8a808c7dce383ad822.png)