一、模型概览

扩散模型的灵感来自于非平衡热力学。定义了一个扩散步骤的马尔可夫链（当前状态只与上一时刻的状态有关），慢慢地向真实数据中添加随机噪声（前向过程），然后学习反向扩散过程（逆扩散过程），从噪声中构建所需的数据样本。

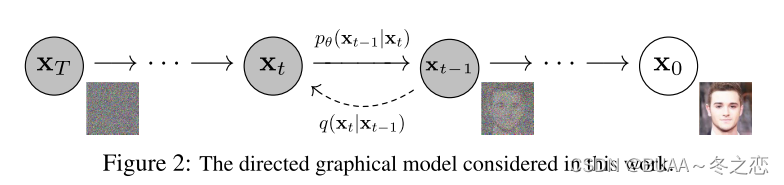
扩散模型有两个过程，分别为扩散过程和逆扩散过程。

如上图所示，扩散过程为从右到左$(X_0\to X_T)$的过程，表示对图片逐渐加噪，且$X_{t+1}$是在$X_t$上加噪得到的，其只受$X_t$的影响，因此扩散过程是一个马尔科夫过程。$X_0$表示从真实数据集中采样得到的一张图片，对$X_0$添加$T$次噪声，图片逐渐变得模糊，当$T$足够大时，$X_T$为标准正态分布。在训练过程中，每次添加的噪声是已知的，即$q(X_t|X_{t-1})$是已知的，根据马尔科夫过程的性质，我们可以递归得到$q(X_t|X_0)$，即$q(X_t|X_0)$是已知的。扩散过程最主要的就是$q(X_t|X_0)$和$q(X_t|X_{t-1})$的推导，推导细节见下文的扩散过程。

如上图所示，逆扩散过程为从左到右$(X_T\to X_0)$的过程，表示从噪声中逐渐复原出图片。如果我们能够在给定$X_t$条件下知道$X_{t-1}$的分布，即如果我们可以知道$q(X_{t-1}|X_t)$，那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。显然我们很难知道$q(X_{t-1}|X_t)$，因此我们才会用$p_{\Theta }(X_{t-1}|X_t)$来近似$q(X_{t-1}|X_t)$，$p_{\Theta }(X_{t-1}|X_t)$就是我们要训练的网络，在原文中就是个U-Net。而很妙的是，虽然我们不知道$q(X_{t-1}|X_t)$，但是$q(X_{t-1}|X_t{X}_0)$却是可以用$q(X_t|X_0)$和$q(X_t|X_{t-1})$表示的，即$q(X_{t-1}|X_t{X}_0)$是可知的，因此我们可以用$q(X_{t-1}|X_t{X}_0)$来指导$p_{\Theta }(X_{t-1}|X_t)$进行训练。逆扩散过程最主要的就是$q(X_{t-1}|X_t{X}_0)$的推导，推导细节见下文的逆扩散过程。

二、扩散过程

如上图所示，扩散过程为从右到左$(X_0\to X_T)$的过程，表示对图片逐渐加噪，它是不含可学习参数的，且$X_{t+1}$是在$X_t$上加噪得到的，其只受$X_t$的影响，因此扩散过程是一个马尔科夫过程。且每一步扩散的步长受变量 { β t ∈ ( 0 , 1 ) } t = 1 T \{β_{t} \in (0,1)\}_{t=1}^{T} {βt​∈(0,1)}t=1T​的影响，且${\beta }_1<{\beta }_2<\cdots <{\beta }_T$，这意味着所加的噪声是越来越大的。$q(X_t|X_{t-1})$可写为如下形式，即给定$X_{t-1}$的条件下，$X_t$服从均值为$\sqrt{1-{\beta }_t}{X}_{t-1}$ ，方差为${\beta }_{t}I$的正态分布:$$q(X_t|X_{t-1})=N(X_t;\sqrt{1-{\beta }_t}{X}_{t-1},{\beta }_{t}I)$$用重参数化技巧表示$X_t$，令${\alpha }_t=1-{\beta }_t$，$Z_t\sim N(0,1),t\ge 0$，即：$$X_t=\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{Z}_{t-1}$$为了计算$q(X_t|X_0)$，首先由于定义为马尔可夫链，所以给定$x_0$条件下$x_{1:T}$的联合概率分布为$$q(X_{1:T}|X_0)=\prod _{t=1}^{T}q(X_t|X_{t-1})$$上述式子计算$q(X_t|X_0)$需要不断迭代，我们希望给定$X_0,{\beta }_t$就可以计算出来。给定${\alpha }_t=1-{\beta }_t,{\bar{\alpha }}_t={\prod }_{t=1}^T{\alpha }_t$，则有：$$\begin{array}{rl}{X}_t& =\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{Z}_{t-1}\\ & =\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{Z}_{t-2})+\sqrt{1-{\alpha }_t}{Z}_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{Z}_{t-2}+\sqrt{1-{\alpha }_t}{Z}_{t-1}(由于两个正态分布X\sim N({\mu }_1,{\sigma }_1),Y\sim N({\mu }_2,{\sigma }_2)叠加后的分布aX+bY的均值是a{\mu }_1+b{\mu }_2，方差是a^2{\sigma }_1^2+b^2{\sigma }_2^2，所以\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{Z}_{t-2}+\sqrt{1-{\alpha }_t}{Z}_{t-1}的均值为0，方差为1-{\alpha }_t{\alpha }_{t-1}，再利用重参数化)\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{Z}}_{t-2}(这里{\bar{Z}}_{t-2}不同于Z_{t-2})\\ & =\cdots \\ & =\sqrt{{\bar{\alpha }}_t}{X}_0+\sqrt{1-{\bar{\alpha }}_t}\bar{Z}\end{array}$$所以，$$X_t=\sqrt{{\bar{\alpha }}_t}{X}_0+\sqrt{1-{\bar{\alpha }}_t}\bar{Z},\bar{Z}\sim N(0,I)$$$$q(X_t|X_0)=N(X_t;\sqrt{{\bar{\alpha }}_t}{X}_0,(1-{\bar{\alpha }}_t)I)$$至此，我们推出了$q(X_t|X_{t-1})$和$q(X_t|X_0)$。

三、逆扩散过程

如果我们能够在给定$X_t$条件下知道$X_{t-1}$的分布，即如果我们可以知道$q(X_{t-1}|X_t)$，那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。显然我们很难知道$q(X_{t-1}|X_t)$，因此我们才会用$p_{\Theta }(X_{t-1}|X_t)$来近似$q(X_{t-1}|X_t)$，$p_{\Theta }(X_{t-1}|X_t)$就是我们要训练的网络。由于扩散过程中我们每次加的噪声很小，所以我们假设$p_{\Theta }(X_{t-1}|X_t)$也是一个高斯分布，可以使用神经网络进行拟合，逆过程也是一个马尔科夫链过程。$$p_{\Theta }(X_{t-1}|X_t)=N(X_{t-1};{\mu }_{\theta }(X_t,t),{\Sigma }_{\theta }(X_t,t))$$$$p_{\Theta }(X_{0:T})=p(X_T)\prod _{t=1}^T{p}_{\theta }(X_{t-1}|X_t)$$

而很妙的是，虽然我们不知道$q(X_{t-1}|X_t)$，但是$q(X_{t-1}|X_t{X}_0)$却是可以用$q(X_t|X_0)$和$q(X_t|X_{t-1})$表示的，即$q(X_{t-1}|X_t{X}_0)$是可知的。下面对$q(X_{t-1}|X_t{X}_0)$进行推导:$$\begin{array}{rl}q(X_{t-1}|X_t{X}_0)& =\frac{q(X_0{X}_{t-1}{X}_t)}{q(X_0{X}_t)}\\ & =\frac{q(X_0{X}_{t-1}{X}_t)}{q(X_0{X}_{t-1})}\frac{q(X_0{X}_{t-1})}{q(X_0{X}_t)}\\ & =q(X_t|X_{t-1}{X}_0)\ast \frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}\end{array}$$由于扩散过程是马尔科夫过程，因此$$q(X_t|X_{t-1}{X}_0)=q(X_t|X_{t-1})$$$$q(X_{t-1}|X_t{X}_0)=q(X_t|X_{t-1})\ast \frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}$$至此，已经把$q(X_{t-1}|X_t{X}_0)$用$q(X_t|X_0)$和$q(X_t|X_{t-1})$进行表示，下面对$q(X_{t-1}|X_t{X}_0)$的表达式进行推导:$$q(X_t|X_{t-1})=N(X_t;\sqrt{1-{\beta }_t}{X}_{t-1},{\beta }_{t}I)=\frac{1}{\sqrt{2\pi (1-{\alpha }_t)}}exp\left(-\frac{1}{2}\frac{(X_t-\sqrt{{\alpha }_t}{X}_{t-1}{)}^2}{1-{\alpha }_t}\right)$$$$q(X_t|X_0)=N(X_t;\sqrt{{\bar{\alpha }}_t}{X}_0,(1-{\bar{\alpha }}_t)I)=\frac{1}{\sqrt{2\pi (1-{\bar{\alpha }}_t)}}exp\left(-\frac{1}{2}\frac{(X_t-\sqrt{{\bar{\alpha }}_t}{X}_0{)}^2}{1-{\bar{\alpha }}_t}\right)$$$$q(X_{t-1}|X_0)=N(X_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{X}_0,(1-{\bar{\alpha }}_{t-1})I)=\frac{1}{\sqrt{2\pi (1-{\bar{\alpha }}_{t-1})}}exp\left(-\frac{1}{2}\frac{(X_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{X}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}\right)$$
$$q(X_{t-1}|X_t{X}_0)=\frac{1}{\sqrt{2\pi \frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t}}exp\left(-\frac{1}{2\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t}{X}_{t-1}^2-2\left(\frac{(1-{\bar{\alpha }}_{t-1})\sqrt{{\alpha }_t}{X}_t}{1-{\bar{\alpha }}_t}+\frac{{\beta }_t\sqrt{{\bar{\alpha }}_{t-1}}{X}_0}{1-{\bar{\alpha }}_t}\right)X_{t-1}+C(X_0,X_t)\right)$$$$q(X_{t-1}|X_t{X}_0)=N\left(X_{t-1};\frac{(1-{\bar{\alpha }}_{t-1})\sqrt{{\alpha }_t}{X}_t}{1-{\bar{\alpha }}_t}+\frac{{\beta }_t\sqrt{{\bar{\alpha }}_{t-1}}{X}_0}{1-{\bar{\alpha }}_t},\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t\right)$$因为$$X_t=\sqrt{{\bar{\alpha }}_t}{X}_0+\sqrt{1-{\bar{\alpha }}_t}Z,Z\sim N(0,I)$$所以$$\begin{array}{rl}\bar{\mu }(X_t,X_0)& =\frac{(1-{\bar{\alpha }}_{t-1})\sqrt{{\alpha }_t}{X}_t}{1-{\bar{\alpha }}_t}+\frac{{\beta }_t\sqrt{{\bar{\alpha }}_{t-1}}{X}_0}{1-{\bar{\alpha }}_t}\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{X}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\left(\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left(X_t-\sqrt{1-{\bar{\alpha }}_t}Z\right)\right)\#(已知X_t的情况下，X_0可以用X_t表示)\\ & =\frac{{\alpha }_t(1-\frac{{\bar{\alpha }}_t}{{\alpha }_t})}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{X}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}(1-{\alpha }_t)}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\alpha }_t}\sqrt{{\bar{\alpha }}_{t-1}}}\left(X_t-\sqrt{1-{\bar{\alpha }}_t}Z\right)\\ & =\frac{{\alpha }_t-{\bar{\alpha }}_t+1-{\alpha }_t}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{X}_t-\frac{1-{\alpha }_t}{\sqrt{{\alpha }_t}\sqrt{1-{\bar{\alpha }}_t}}Z\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left(X_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}Z\right)\end{array}$$所以$$q(X_{t-1}|X_t{X}_0)=N\left(X_{t-1};\frac{1}{\sqrt{{\alpha }_t}}\left(X_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}Z\right),\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t\right),Z\sim N(0,I)$$至此，得到了$q(X_{t-1}|X_t{X}_0)$的分布表达式。接下来，我们介绍怎么用$q(X_{t-1}|X_t{X}_0)$来监督$p_{\Theta }(X_{t-1}|X_t)$进行训练。