目录
- 1. 作者介绍
- 2. LDA和PCA算法介绍
- 2.1 LDA算法
- 2.2 PCA算法
- 2.3 两个算法的区别与联系
- 3. 实验过程
- 3.1 数据集介绍
- 3.2 算法流程
- 3.3 核心算法介绍
- 3.4 完整代码
- 3.5 实验结果与分析
1. 作者介绍
王鑫,男,西安工程大学电子信息学院,2022级研究生
研究方向:机器视觉与人工智能
电子邮件:30581433@qq.com
路治东,男,西安工程大学电子信息学院,2022级研究生,张宏伟人工智能课题组
研究方向:机器视觉与人工智能
电子邮件:2063079527@qq.com
2. LDA和PCA算法介绍
2.1 LDA算法
LDA(线性判别式分析 Linear Discriminant Analysis)是一个经典的 二分类算法,属于机器学习中的监督学习算法,常用来做特征提取、数据降 维和任务分类。在人脸识别、人脸检测等领域发挥重要作用。
主要思想:给定训练样本集,设法将样本投影到一条直线上,使得同类 的样本的投影尽可能的接近、异类样本的投影尽可能的远离(即最小化类内 距离和最大化类间距离)。
2.2 PCA算法
PCA全称为主成分分析算法,是最常用的线性降维方法,它的目标是通过某种线性投影, 将高维的数据映射到低维的空间中,并期望在所投影的维度上数据的信息量最大(方差最大), 以此使用较少的数据维度,同时保留住较多的原数据点的特性。
PCA降维的目的,就是为了在尽量保证“信息量不丢失”的情况下,对原始特征进行降维,也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影。将原特征投影到这些维度 上,使降维后信息量损失最小。
2.3 两个算法的区别与联系
相同点:
1.均是降维方法。
2.降维时均使用了矩阵特征分解的思想。
3.两者都假设数据符合高斯分布。
不同点:
1.PCA是无监督的降维方法,而LDA是有监督的降维方法。
2.LDA除了可以降维,还可以用于分类。
3.LDA降维最多降到类别数 k-1的维数(k是样本类别的4.LDA选择的是分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
这点从下图1可以形象的看出,在某些数据分布下LDA比PCA降维较优。然而,某些某些数据分布下PCA比LDA降维较优,如下图2所示所示:

3. 实验过程
3.1 数据集介绍
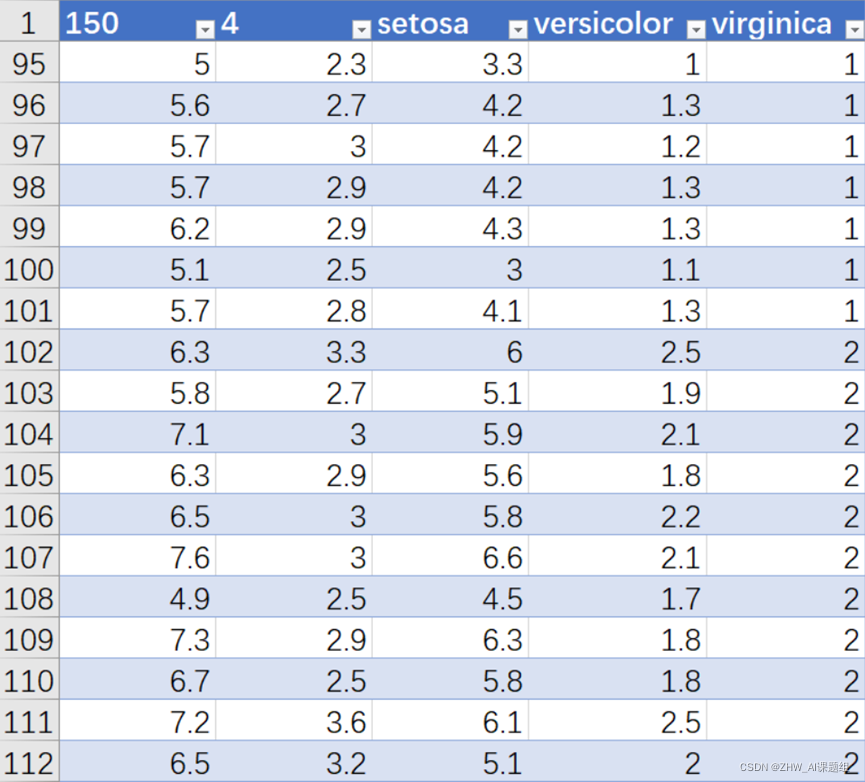
Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预 测鸢尾花卉属于(Setosa(山鸢尾),Versicolour(杂色鸢尾),Virginica(维吉尼亚鸢尾))三个种类中的哪一类。鸢尾花(iris) 数据集,它共有4个属性列和一个品种类别列:sepal length(萼片长度)、sepal width(萼片宽度)、petal length(花瓣 长度)、petal width (花瓣宽度),单位都是厘米。3个品种类别是Setosa、Versicolour、Virginica,样本数量150个,每 类50个。

数据集的部分数据如图所示
3.2 算法流程
基于LDA与PCA算法的鸢尾花数据集二维投影比较的算法实现流程如下:
1.加载鸢尾花数据集:使用相关库加载鸢尾花数据集,包括特征向量和对应的类别标签。
2.LDA降维:使用LDA算法对特征向量进行降维。首先,计算各个类别的均值向量和类内散度矩阵。然后,计算类间散度矩阵,并求解广义特征值问题,得到投影方向(特征向量)。选择最大的k个特征值对应的特征向量作为投影方向,其中k是要降低到的维度数。最后,使用选定的投影方向将特征向量映射到新的低维空间中,得到降维后的数据。
3.PCA降维:使用PCA算法对特征向量进行降维。首先,对特征向量进行均值中心化处理。然后,计算特征向量的协方差矩阵。接下来,求解协方差矩阵的特征值和特征向量。选择最大的k个特征值对应的特征向量作为投影方向,其中k是要降低到的维度数。最后,使用选定的投影方向将特征向量映射到新的低维空间中,得到降维后的数据。
4.绘制结果:使用可视化库绘制两种降维方法得到的二维投影结果。可以使用散点图展示不同类别的样本,使用不同的颜色标记不同的类别。
5.比较结果:将LDA和PCA的投影结果放在同一个画面中进行比较。可以使用子图来分别显示LDA和PCA的结果,或者使用不同的颜色或标记在同一个子图中展示两种方法的结果。
通过比较LDA和PCA的降维结果,可以观察它们在鸢尾花数据集上的效果差异,以及它们在保留数据信息和类别可分性方面的表现。
3.3 核心算法介绍
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data #将鸢尾花数据集的特征数据存储在X变量中
y = iris.target #将鸢尾花数据集的标签存储在y变量中
target_names = iris.target_names #将鸢尾花数据集的目标类别名称存储在target_names变量中
# 使用LDA进行降维
lda = LinearDiscriminantAnalysis(n_components=2) #创建一个LinearDiscriminantAnalysis对象,指定要降到的维度为2
X_lda = lda.fit_transform(X, y) # 使用线性判别分析对特征数据进行降维,得到降维后的结果存储在X_lda变量中
# 使用PCA进行降维
pca = PCA(n_components=2) #创建一个PCA对象,指定要降到的维度为2
X_pca = pca.fit_transform(X) #使用主成分分析对特征数据进行降维,得到降维后的结果存储在X_pca变量中
加载鸢尾花数据集,将鸢尾花数据集的特征数据存储在X变量中,将鸢尾花数据集的标签存储在y变量中,将鸢尾花数据集的目标类别名称存储在target_names变量中。
创建一个LinearDiscriminantAnalysis对象,指定要降到的维度为2;使用线性判别分析对特征数据进行降维,得到降维后的结果存储在X_lda变量中;创建一个PCA对象,指定要降到的维度为2;使用主成分分析对特征数据进行降维,得到降维后的结果存储在X_pca变量中。
# 绘制LDA结果
plt.figure(figsize=(12, 6)) #创建一个图形窗口,指定图形的大小为12x6
plt.subplot(121) #创建一个子图,在整个图形窗口中创建一个1x2的子图布局,并定位到第一个子图
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): #迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素。zip()函数用于将这三个列表中的对应元素组合在一起,使得在每次循环中,color、i和target_name分别表示三个列表中对应位置的元素
plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], color=color, alpha=.8, lw=2, label=target_name) #使用scatter()函数绘制LDA降维后的结果的散点图。X_lda[y == i, 0]表示选择标签值等于i的样本在降维结果中的第一维度数据,X_lda[y == i, 1]表示选择标签值等于i的样本在降维结果中的第二维度数据。color表示散点图的颜色,alpha表示散点图的透明度,lw表示散点图中点的边框线宽度,label表示每个散点图的标签。
plt.legend(loc='best', shadow=False, scatterpoints=1) #添加图例,loc='best'表示图例放置在最佳位置,shadow=False表示不显示图例的阴影,scatterpoints=1表示图例中只显示一个散点
plt.title('LDA of IRIS dataset') #添加子图的标题为'LDA of IRIS dataset'
# 绘制PCA结果
plt.subplot(122) #定位到第二个子图
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): #同样地,迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=.8, lw=2, label=target_name) #使用scatter()函数绘制PCA降维后的结果的散点图。与步骤17类似,但是这里是使用PCA降维后的结果进行绘制
plt.legend(loc='best', shadow=False, scatterpoints=1) # 添加图例
plt.title('PCA of IRIS dataset') #添加子图的标题为'PCA of IRIS dataset'
创建一个图形窗口,指定图形的大小为12x6;创建一个子图,在整个图形窗口中创建一个1x2的子图布局,并定位到第一个子图;迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素。zip()函数用于将这三个列表中的对应元素组合在一起,使得在每次循环中,color、i和target_name分别表示三个列表中对应位置的元素;使用scatter()函数绘制LDA降维后的结果的散点图。X_lda[y = =i, 0]表示选择标签值等于i的样本在降维结果中的第一维度数据,X_lda[y = = i, 1]表示选择标签值等于i的样本在降维结果中的第二维度数据。color表示散点图的颜色,alpha表示散点图的透明度,lw表示散点图中点的边框线宽度,label表示每个散点图的标签;添加图例,loc=‘best’表示图例放置在最佳位置,shadow=False表示不显示图例的阴影,scatterpoints=1表示图例中只显示一个散点;添加子图的标题为’LDA of IRIS dataset‘。
定位到第二个子图;同样地,迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素;使用scatter()函数绘制PCA降维后的结果的散点图。与前面类似,但是这里是使用PCA降维后的结果进行绘制;添加图例;添加子图的标题为‘PCA of IRIS dataset’。
3.4 完整代码
import numpy as np
import matplotlib.pyplot as plt #导入Matplotlib库的pyplot模块,用于绘制图形
from sklearn import datasets #从Scikit-learn库中导入datasets模块,用于加载数据集
from sklearn.decomposition import PCA #从Scikit-learn库中导入PCA模块,用于主成分分析降维
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis #从Scikit-learn库中导入LinearDiscriminantAnalysis模块,用于线性判别分析降维
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data #将鸢尾花数据集的特征数据存储在X变量中
y = iris.target #将鸢尾花数据集的标签存储在y变量中
target_names = iris.target_names #将鸢尾花数据集的目标类别名称存储在target_names变量中
# 使用LDA进行降维
lda = LinearDiscriminantAnalysis(n_components=2) #创建一个LinearDiscriminantAnalysis对象,指定要降到的维度为2
X_lda = lda.fit_transform(X, y) # 使用线性判别分析对特征数据进行降维,得到降维后的结果存储在X_lda变量中
# 使用PCA进行降维
pca = PCA(n_components=2) #创建一个PCA对象,指定要降到的维度为2
X_pca = pca.fit_transform(X) #使用主成分分析对特征数据进行降维,得到降维后的结果存储在X_pca变量中
# 绘制LDA结果
plt.figure(figsize=(12, 6)) #创建一个图形窗口,指定图形的大小为12x6
plt.subplot(121) #创建一个子图,在整个图形窗口中创建一个1x2的子图布局,并定位到第一个子图
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): #迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素。zip()函数用于将这三个列表中的对应元素组合在一起,使得在每次循环中,color、i和target_name分别表示三个列表中对应位置的元素
plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], color=color, alpha=.8, lw=2, label=target_name) #使用scatter()函数绘制LDA降维后的结果的散点图。X_lda[y == i, 0]表示选择标签值等于i的样本在降维结果中的第一维度数据,X_lda[y == i, 1]表示选择标签值等于i的样本在降维结果中的第二维度数据。color表示散点图的颜色,alpha表示散点图的透明度,lw表示散点图中点的边框线宽度,label表示每个散点图的标签。
plt.legend(loc='best', shadow=False, scatterpoints=1) #添加图例,loc='best'表示图例放置在最佳位置,shadow=False表示不显示图例的阴影,scatterpoints=1表示图例中只显示一个散点
plt.title('LDA of IRIS dataset') #添加子图的标题为'LDA of IRIS dataset'
# 绘制PCA结果
plt.subplot(122) #定位到第二个子图
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): #同样地,迭代处理颜色列表、[0, 1, 2]列表和目标类别名称列表中的元素
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=.8, lw=2, label=target_name) #使用scatter()函数绘制PCA降维后的结果的散点图。与步骤17类似,但是这里是使用PCA降维后的结果进行绘制
plt.legend(loc='best', shadow=False, scatterpoints=1) # 添加图例
plt.title('PCA of IRIS dataset') #添加子图的标题为'PCA of IRIS dataset'
# 显示图形
plt.tight_layout() #调整子图的布局,使其紧凑显示
plt.show() #显示图形
该代码的作用是加载鸢尾花数据集,使用LDA和PCA算法对数据进行降维,然后将降维结果分别绘制在两个子图中,其中LDA结果在左侧,PCA结果在右侧。
每个子图中的散点图表示不同类别的样本,并通过图例进行标注。最后,显示图形并呈现比较结果。
3.5 实验结果与分析

基于鸢尾花数据集的LDA和PCA二维投影的比较总结如下:
LDA在保留类别信息方面表现优秀。LDA通过最大化类间散度和最小化类内散度,能够在降维的同时最大化不同类别之间的可分性。在二维投影中,LDA能够有效地将不同鸢尾花类别分开,并展现出明显的聚类效果。
PCA在数据展示和压缩方面具有优势。PCA通过选择方差最大的投影方向,能够在保留数据的主要信息的同时,实现较好的数据压缩效果。在二维投影中,PCA将数据集分布在两个主要方向上,并显示出数据的整体分布情况。
综上所述,对于鸢尾花数据集,LDA在保留类别信息和类别区分方面表现出色,而PCA则更适合用于数据的展示和压缩。根据具体任务需求,我们可以选择适合的降维算法来获得最佳的数据表示。