机器学习——KNN算法（手动代码，含泪）

news2024/10/6 16:17:17

徒手实现代码的过程，真是含泪和心酸，浪费了生命中的三天，以及工作中的划水一小时
终于滤清思路后，自己实现了KNN
都说KNN是最基础，最简单的分类器
放屁！骗纸！！！它的想法是简单的，但实现的过程何其复杂！！！
问题何其之多！！是我实现感知机、逻辑回归分类、线性回归、朴素贝叶斯中，最难实现的分类算法！！！！
给多少时间都无法将这个槽吐尽，甚至算法都没完全弄好，但只剩收尾工作了

1. KNN 分类思想

首先，KNN思想很简单，找到离目标对象最近的K个对象，以K个对象中数量最多的那个类型为预测结果。

就好像：要对一个有喉结、短头发、平胸的对象进行性别的分类，那么特征最相近的K个人，如果男性居多，则将该对象分类为男性。如果女性居多，则分类为女性。

KNN搜索特征最相近的精髓，在于建立KD树——二叉树

2. KNN 分类流程

2.1 构建KD树

构建KD树的原因是，我们不能逐一去计算某个对象与所有对象的特征距离。

那就对所有对象的特征，进行KD树的分组，分组规则别人说的非常清晰明了，我看了之后有种恍然大悟、拍手叫好的激动
kd树的搜索过程到底是怎么进行的？ - 月来客栈的文章 - 知乎

但是当我自己去实现时，遇到重重的困难

先来实现 KD树：应用二叉树的原理

# 构建一个二叉树节点
class Node_1():
    def __init__(self,X_value):
        self.left = None
        self.right = None
        self.value = []
        self.X = X_value # {"特证名":"x","划分标准":"aaaaaa"}
# 根据节点，构建一个二叉树
class Tree():
    def __init__(self):
        self.root = None
    def get_value_1(self,X_arg,node_arg=None):
        node = node_arg
        if self.root == None:
            node = Node_1(X_arg)
            self.root = node
        # 获取所有特征各自对应的方差
        vars = [X_arg[i].var() for i in X_arg.columns[0:2]]
        # 如果这些方差中，最大的那个方差为0或是无法计算，则说明数据已经分的很清楚了
        """重点：停止迭代的条件：所有特征的方差均为0 或无法计算"""
        if max(vars) == 0 or math.isnan(max(vars)):
            return
        """以方差最大的那个特征，作为分组的维度，根据该特征的中位数进行分组:
        pandas中的median中位数，与统计学稍微不同
        统计学中偶数个数据的中位数，是中间两个数据的均值
        pandas中偶数个数据的中位数，是中间两个数据的其中一个
        因此，用pandas的median计算中位数，还需要考虑一个非常坑的问题：如果最后只剩两个数据，中位数到底是偏大的那个，还是偏小的那个，这决定了我们分组到底能不能分清楚！！！"""   
        X_name = X_arg.columns[vars.index(max(vars))]
        med = X_arg[X_name].median()
        if med == X_arg[X_name].max():
            """要根据中位数，分为左组、右组：涉及到pandas的分组条件筛选【抄网上】"""
            left = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] < med].index]).reset_index(drop=True)
            right = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] >= med].index]).reset_index(drop=True)
        else:
            left = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] <= med].index]).reset_index(drop=True)
            right = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] > med].index]).reset_index(drop=True)
        """如果左右组有一个为空，说明这个节点已经分完了"""
        if left.empty or right.empty:
            return
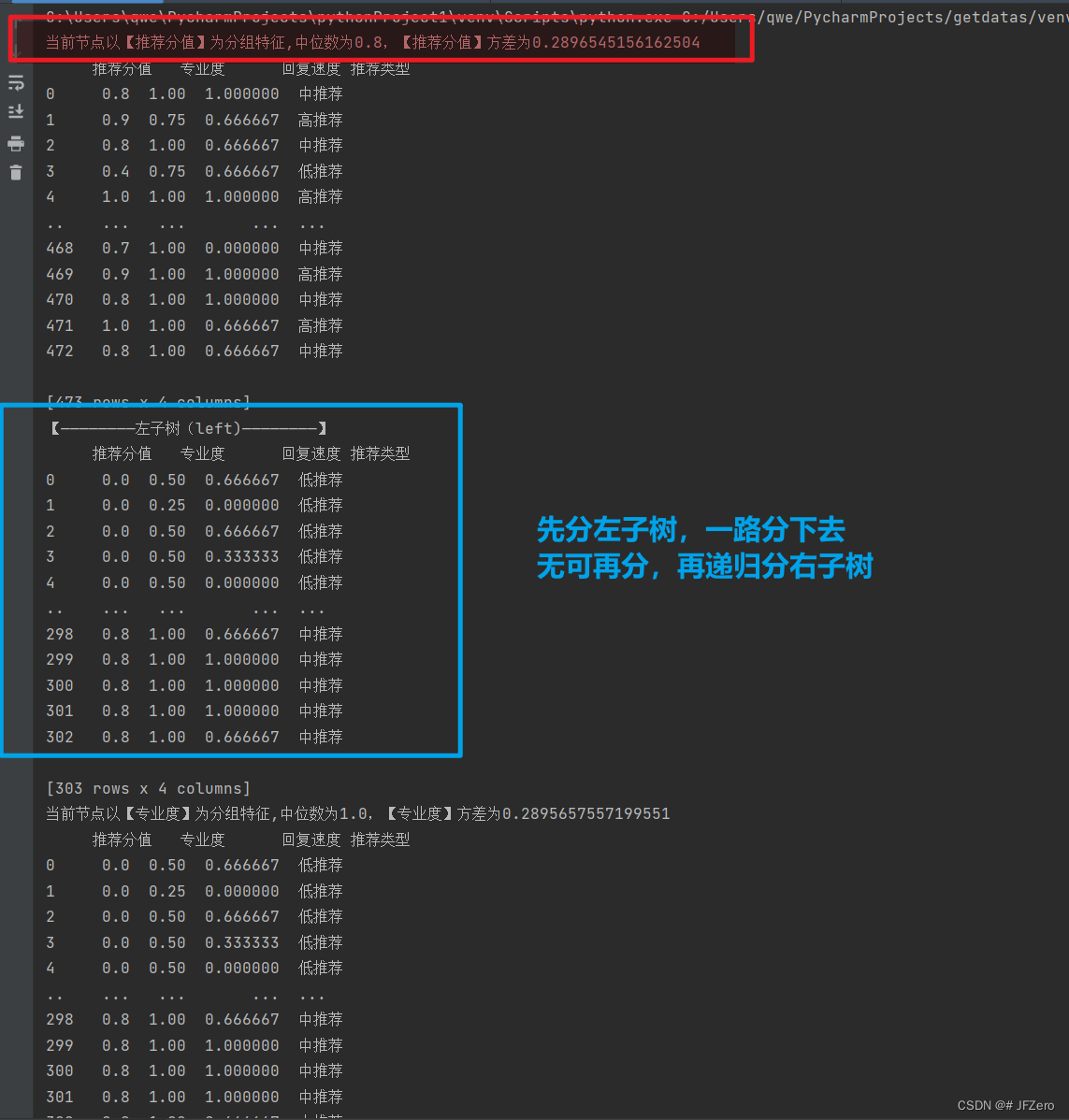
        # print(f"当前节点以【{X_name}】为分组特征,中位数为{med}，【{X_name}】方差为{X_arg[X_name].std()}")
        # print(X_arg)
        node.value=[X_name,med]
        # print(f"【————————左子树（left)————————】")
        # print(left)
        node_left = Node_1(left)
        node.left = node_left
        self.get_value_1(left, node_left)
        # print(f"【————————右子树(right)————————】")
        # print(right)
        node_right = Node_1(right)
        node.right = node_right
        self.get_value_1(right, node_right)

分的过程，很漂亮，我看了很多次。。。肉眼数它是怎么分的！！！瞎了
在这里插入图片描述

最终分组后的数据，都分在叶子节点上【全挂在树梢，中间节点不挂】

2.2 搜索最近邻&K近邻

搜索最近邻和K近邻也并不容易，用到了递归

我现在对递归，真的是轻车熟路！！！！
痛苦，总是让人印象深刻

最近邻，主要还是用到了欧式距离的计算

class Find_KD_Tree:
    def __init__(self):
        self.k = 10
        self.K_list = []
        self.min_point = []
        # self.X = X_arg
    def find_K(self,node_arg, X_arg):
        # global k, K_list, min_point
        columns_1 = len(node_arg.X.columns)
        if not node_arg.value:
            k_distance = ((node_arg.X.loc[0][0:columns_1 - 1] - X_arg[0:columns_1 - 1]) ** 2).sum()
            if (not self.min_point) or (k_distance < self.min_point[0]):  # 当没有最小值，或比最小值更小时
                self.min_point = [k_distance, node_arg]
            if len(self.K_list) < self.k:
                row, columns = node_arg.X.shape
                for i in range(row):
                    # print(f"添加的距离为{k_distance},添加的数据为")
                    # print(node_arg.X.loc[i])
                    if len(self.K_list) <= self.k:
                        self.K_list.append([k_distance, node_arg.X.loc[i]])
                        self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    elif k_distance < self.K_list[-1][0]:
                        # print(f"出现了替代值{k_distance},当前列表最末为{[i[0] for i in self.K_list]}")
                        self.K_list.pop()
                        self.K_list.append([k_distance, node_arg.X.loc[i]])
                        self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    else:
                        break
                        # print(K_list)
                        # K_list.sort()
            elif k_distance < self.K_list[-1][0]:
                row, columns = node_arg.X.shape
                for i in range(row):
                    # print(f"添加的距离为{k_distance},添加的数据为")
                    # print(node_arg.X.loc[i])
                    # print(f"出现了替代值{k_distance},当前列表最末为{[i[0] for i in K_list]}")
                    self.K_list.pop()
                    self.K_list.append([k_distance, node_arg.X.loc[i]])
                    self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    if k_distance > self.K_list[-1][0]:
                        break
                # print(K_list)
                # K_list.sort()
        else:
            # 计算叶子与当前数据的欧式距离：叶子上都是一样的数据，选择其中一个数据与当前数据进行计算即可。
            X_name = node_arg.value[0]
            X_value = node_arg.value[1]
            node_distance = (X_arg[X_name] - X_value) ** 2
            # print("cecece测试",node_distance)
            # 选择方向-回溯搜索K近邻
            if X_arg[X_name] <= X_value:
                # print(f'当前节点按{X_name}来分，且往左节点搜索')
                self.find_K(node_arg.left, X_arg)
                # print(f'当前节点距维度的距离为{node_distance},最近邻距离min为{self.min_point[0]}')
                if node_distance <= self.min_point[0]:
                    # print(f'当前节点按{X_name}来分，且可往右right右节点，有可能搜索到近邻k')
                    self.find_K(node_arg.right, X_arg)
            else:
                # print(f'当前节点按{X_name}来分，且往右节点搜索')
                self.find_K(node_arg.right, X_arg)
                # print(f'当前节点距维度的距离为{node_distance},最近邻距离min为{self.min_point[0]}')
                if node_distance <= self.min_point[0]:
                    # print(f'当前节点按{X_name}来分，且可往右left左节点，有可能搜索到近邻k')
                    self.find_K(node_arg.left, X_arg)

最终将每一条数据的K近邻，存储在一个二维列表中，输出结果如下

有些K近邻的列表，不足k个（我设为10个）元素，主要还是因为回溯到上一个维度时，维度距离超过了全局最小距离，因此就不再搜索另一边的树了。
搜索最近邻和K近邻的过程，比较简单：（主要是要细讲逻辑，太复杂了。。。放弃细讲。。。）

在这里插入图片描述

2.3 预测分类

最终，只需要将上述每个对象的K近邻，通过统计，得出它们各自类型最多的那个分类，即为预测分类的结果。

相比于前边徒手建立二叉树，和徒手进行K近邻、最近邻的回溯搜索来说，这一步真是太过easy，我都已经不稀罕浪费脑细胞来详写了！！！

待回头，收拾旧心情，再来写

3. KNN - 手动代码（缺2.3）

""" 难点：构思要如何建立KD树，如何回溯找出最近邻和K近邻"""
import math
import time
import pandas as pd


# 获取所需数据：'推荐分值', '专业度','回复速度','用户群活跃天数'
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐类型','推荐分值', '专业度','回复速度']
datas_1 = datas[important_features]

# 明确实值Y为'推荐分值'，X分别为'专业度','回复速度','用户群活跃天数'
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)
# X 归一化处理
data = (X-X.min())/(X.max()-X.min())
data["推荐类型"] = Y
# print(data)
"""
构建KNN二叉树
# 构造二叉树的节点、构造二叉树的内容
    ① 二叉树的节点是node：包含 4 个属性 - 值value、左left、右left、数据组
    ② 二叉树的内容是三个节点：根节点、左节点、右节点
# 迭代创建二叉树的三个关键：
    ① 停止迭代的条件：特征方差为0或Nan（无法计算方差）
    ② 如何分组迭代：选择方差最大的特征，按该特征的中位数，对数据进行分组，再对组调用构造二叉树的方法
"""



# 构建一个二叉树节点
class Node_1():
    def __init__(self,X_value):
        self.left = None
        self.right = None
        self.value = []
        self.X = X_value # {"特证名":"x","划分标准":"aaaaaa"}
# 根据节点，构建一个二叉树
class Tree():
    def __init__(self):
        self.root = None
    def get_value_1(self,X_arg,node_arg=None):
        node = node_arg
        if self.root == None:
            node = Node_1(X_arg)
            self.root = node
        vars = [X_arg[i].var() for i in X_arg.columns[0:2]]
        if max(vars) == 0 or math.isnan(max(vars)):
            return
        X_name = X_arg.columns[vars.index(max(vars))]
        med = X_arg[X_name].median()
        if med == X_arg[X_name].max():
            """要根据中位数，分为左组、右组：涉及到pandas的分组条件筛选"""
            left = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] < med].index]).reset_index(drop=True)
            right = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] >= med].index]).reset_index(drop=True)

        else:
            left = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] <= med].index]).reset_index(drop=True)
            right = X_arg.groupby(X_name).apply(lambda x: x.loc[x.loc[x[X_name] > med].index]).reset_index(drop=True)
        if left.empty or right.empty:
            return
        print(f"当前节点以【{X_name}】为分组特征,中位数为{med}，【{X_name}】方差为{X_arg[X_name].std()}")
        print(X_arg)
        node.value=[X_name,med]


        print(f"【————————左子树（left)————————】")
        print(left)
        node_left = Node_1(left)
        node.left = node_left
        self.get_value_1(left, node_left)

        #
        print(f"【————————右子树(right)————————】")
        print(right)
        node_right = Node_1(right)
        node.right = node_right
        self.get_value_1(right, node_right)

    def pre_print(self,root):
        if root is None:
            return
        # if not root.left and not root.right:
        #     print(f"现在root的节点按【{root.X}】来分")

        # print(f"print：{root.X}")
        self.pre_print(root.left)
        self.pre_print(root.right)




class Find_KD_Tree:
    def __init__(self):
        self.k = 10
        self.K_list = []
        self.min_point = []
        # self.X = X_arg
    def find_K(self,node_arg, X_arg):
        # global k, K_list, min_point
        columns_1 = len(node_arg.X.columns)
        if not node_arg.value:
            k_distance = ((node_arg.X.loc[0][0:columns_1 - 1] - X_arg[0:columns_1 - 1]) ** 2).sum()
            if (not self.min_point) or (k_distance < self.min_point[0]):  # 当没有最小值，或比最小值更小时
                self.min_point = [k_distance, node_arg]
            if len(self.K_list) < self.k:
                row, columns = node_arg.X.shape
                for i in range(row):
                    # print(f"添加的距离为{k_distance},添加的数据为")
                    # print(node_arg.X.loc[i])
                    if len(self.K_list) <= self.k:
                        self.K_list.append([k_distance, node_arg.X.loc[i]])
                        self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    elif k_distance < self.K_list[-1][0]:
                        # print(f"出现了替代值{k_distance},当前列表最末为{[i[0] for i in self.K_list]}")
                        self.K_list.pop()
                        self.K_list.append([k_distance, node_arg.X.loc[i]])
                        self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    else:
                        break
                        # print(K_list)
                        # K_list.sort()
            elif k_distance < self.K_list[-1][0]:
                row, columns = node_arg.X.shape
                for i in range(row):
                    # print(f"添加的距离为{k_distance},添加的数据为")
                    # print(node_arg.X.loc[i])
                    # print(f"出现了替代值{k_distance},当前列表最末为{[i[0] for i in K_list]}")
                    self.K_list.pop()
                    self.K_list.append([k_distance, node_arg.X.loc[i]])
                    self.K_list = sorted(self.K_list, key=lambda cus: cus[0], reverse=False)
                    if k_distance > self.K_list[-1][0]:
                        break
                # print(K_list)
                # K_list.sort()
        else:
            # 计算叶子与当前数据的欧式距离：叶子上都是一样的数据，选择其中一个数据与当前数据进行计算即可。
            X_name = node_arg.value[0]
            X_value = node_arg.value[1]
            node_distance = (X_arg[X_name] - X_value) ** 2
            # print("cecece测试",node_distance)
            # 选择方向-回溯搜索K近邻
            if X_arg[X_name] <= X_value:
                # print(f'当前节点按{X_name}来分，且往左节点搜索')
                self.find_K(node_arg.left, X_arg)
                # print(f'当前节点距维度的距离为{node_distance},最近邻距离min为{self.min_point[0]}')
                if node_distance <= self.min_point[0]:
                    # print(f'当前节点按{X_name}来分，且可往右right右节点，有可能搜索到近邻k')
                    self.find_K(node_arg.right, X_arg)
            else:
                # print(f'当前节点按{X_name}来分，且往右节点搜索')
                self.find_K(node_arg.right, X_arg)
                # print(f'当前节点距维度的距离为{node_distance},最近邻距离min为{self.min_point[0]}')
                if node_distance <= self.min_point[0]:
                    # print(f'当前节点按{X_name}来分，且可往右left左节点，有可能搜索到近邻k')
                    self.find_K(node_arg.left, X_arg)

    def predict(self):
        all_predict.append([i[1][-1] for i in self.K_list])
        # print(f"{[i[1][-1] for i in self.K_list]}")

a = Tree()
a.get_value_1(data)
all_predict = []
# print("____++++++++__________")
# a.pre_print(a.root)
# k = 5

def func(datas_arg):
    # print(datas_arg)
    ob = Find_KD_Tree()
    ob.find_K(a.root,datas_arg)
    # print("++++++++++++++++++++++++++++")
    ob.predict()
data.apply(func,axis = 1)
for i in all_predict:
    print(i)

附：KNN - sklearn代码（too easy)

from sklearn import neighbors
import time
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report

# 获取所需数据：'推荐分值', '专业度','回复速度','用户群活跃天数'
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐类型','推荐分值', '专业度','回复速度','用户群活跃天数']
datas_1 = datas[important_features]

# 明确实值Y为'推荐分值'，X分别为'专业度','回复速度','用户群活跃天数'
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)

start_time = time.time()
# 1. 建立模型
classifier = neighbors.KNeighborsClassifier(10)
classifier.fit(X,Y)

# 2. 学习模型
classifier.fit(X,Y)
Y_predict = classifier.predict(X)
result_P = classifier.predict_proba(X)
end_time = time.time()

# 3. 衡量模型
accurency = classifier.score(X,Y)
PRF = classification_report(Y,Y_predict)


# 输出模型最优状态下的参数及衡量模型的指标
print(f"KNN 耗时{end_time-start_time}秒")
print("KNN的分类【准备率】为：",accurency)
print("KNN的精确率、召回率、F1分数为：")
print(PRF)

print('【模型分类，实际分类】的对比如下：')
for index,value in enumerate(zip(Y_predict,Y)):
    print(value)
    print(result_P[index])
# print(result_P)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/663399.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

第八章——向量代数与空间解析几何

第八章——向量代数与空间解析几何

目录 一、运算公式 二、平面的法线向量 注&#xff1a;加粗体为向量 一、运算公式 1.若a//b&#xff0c;那么aλb 若a⊥b&#xff0c;那么a*b0 2.若A(x1,y1,z1)&#xff0c;B(x2,y2,z2) 中点坐标&#xff1a;AB中点M(x1x2/2,y1y2/2,z1z2/2) 两点间的距离和模的计算&#x…
阅读更多...
第3章 信息系统治理

第3章 信息系统治理

文章目录 3.1.1 IT治理基础1. IT治理的驱动因素2. IT治理的目标价值3. IT治理的管理层次 3.1.2 IT治理体系1. IT治理关键决策2. IT治理体系框架3. IT治理核心内容4. IT治理机制经验&#xff08;建立IT治理机制的原则&#xff1a;简单、透明、适合&#xff09; 3.1.3 IT治理任务…
阅读更多...
工作流引擎Flowable

工作流引擎Flowable

这里写目录标题 1.Flowable基础1.1 入门学习 2.流程图设计器2.1 FlowableUI2.1.1 绘制流程图 1.Flowable基础 官方手册 1.1 入门学习 一、依赖 <dependencies><dependency><groupId>org.flowable</groupId><artifactId>flowable-engine</…
阅读更多...
jenkins——Git版本管理

jenkins——Git版本管理

这里写目录标题 一、Jenkins Git 版本管理1、Git 的集成2、在执行job的机器上安装好Git3、无法连接仓库&#xff0c;问题解决解决方法1&#xff1a;&#xff08;不推荐&#xff09;1、把仓库设置成公开的&#xff0c;然后重新添加仓库地址 解决方法2&#xff1a;通过凭证的方式…
阅读更多...
打破Spring的垄断，云原生Java框架Micronaut

打破Spring的垄断，云原生Java框架Micronaut

文章目录 什么是Micronaut&#xff1f;Micronaut的功能特性相较于Spring的优势 Micronaut框架的使用安装Micronaut cli创建Micronaut项目 Micronaut应用的部署micronaut反应式编程 MCNU云原生&#xff0c;文章首发地&#xff0c;欢迎微信搜索关注&#xff0c;更多干货&#xff…
阅读更多...
基于springboot的文件的上传到本地和云上传（阿里云）

基于springboot的文件的上传到本地和云上传（阿里云）

1.文件上传 1.介绍 文件上传&#xff0c;是指将本地图片、视频、音频等文件上传到服务器&#xff0c;供其他用户浏览或下载的过程。文件上传在项目中应用非常广泛&#xff0c;我们经常发微博、发微信朋友圈都用到了文件上传功能。 2.前端的文件上传–form表单 将静态的页面…
阅读更多...
接口自动化测试面试问题及答案

接口自动化测试面试问题及答案

目录 1.请问你是如何做接口测试的&#xff1f; 2.接口测试如何设计测试用例&#xff1f; 3.接口测试执行中需要比对数据库吗&#xff1f; 4.接口测试质量评估标准是什么&#xff1f; 5.接口产生的垃圾数据如何清理 6.其他接口要先获取接口信息&#xff0c;如何让登录的接口…
阅读更多...
化工园区人员全过程轨迹化安全解决方案

化工园区人员全过程轨迹化安全解决方案

1、项目背景 化工园区化工厂是生产安全重点单位&#xff0c;对人员定位管理需求强烈。对人员定位主要需求是&#xff1a;一般区域人数统计、人员轨迹、重点区域人员实时精准定位。 华安联大安全化工园区人员全过程轨迹化安全解决方案通过人员实时定位管理、移动轨迹追溯、险情…
阅读更多...
《项目实战》构建SpringCloud alibaba项目（二、构建微服务鉴权子工程store-authority-service）

《项目实战》构建SpringCloud alibaba项目（二、构建微服务鉴权子工程store-authority-service）

系列文章目录 构建SpringCloud alibaba项目&#xff08;一、构建父工程、公共库、网关&#xff09; 构建SpringCloud alibaba项目&#xff08;二、构建微服务鉴权子工程store-authority-service&#xff09; 文章目录 系列文章目录前言1、在公共库增加 UserInfo类2、微服务鉴权…
阅读更多...
初识SLAM

初识SLAM

SLAM的作用 想象一个叫小萝卜的机器人&#xff0c;小萝卜在未知环境走&#xff0c;肯定想让小萝卜在脑海中记住两件事&#xff1a; 1. 我在什么地方&#xff1f;——定位。 2. 周围环境是什么样&#xff1f;——建图。 这就和我们逛一个旅游景点一样&#xff0c;我们会潜意识…
阅读更多...
清华青年AI自强作业hw3_3：用NN网络拟合MNIST手写数字分类

清华青年AI自强作业hw3_3：用NN网络拟合MNIST手写数字分类

清华青年AI自强作业hw3_3&#xff1a;用NN网络拟合MNIST手写数字分类 实现过程具体思路多分类网络模型训练结果分析 相关链接 一起学AI系列博客&#xff1a;目录索引 hw3_3&#xff1a;用NN网络拟合MNIST手写数字分类 体会神经网络设计和TF框架编程 对比hw3_1两者的模型、效果…
阅读更多...
CLIP和GPT

CLIP和GPT

CLIP CLIP下游应用&#xff1a;VQGAN、DALL-ECLIP-Event:Connecting Text and Images with Event StructuresHierarchical Text-Conditional Image Generation with CLIP LatentsGPT系列算法GPT-1&#xff1a;GPT-2&#xff1a;GPT-3&#xff1a;GPT-3应用&#xff1a;Evaluati…
阅读更多...
关于Win搜索太慢我自己写了一个Everything

关于Win搜索太慢我自己写了一个Everything

文章目录 前言使用工具使用技术实现功能关于使用的技术比较OUTJDBC构建数据库FileMetasize处理文件最后修改时间equals重写其他方法 dao数据库源头获取连接关闭资源连接 FileDao初始化插入文件/目录到数据库中查询数据删除数据 特殊处理方法实现测试 服务初始化服务方法 操作单…
阅读更多...
简要介绍 | 基于Python的图像形态学处理概述

简要介绍 | 基于Python的图像形态学处理概述

注1&#xff1a;本文系“简要介绍”系列之一&#xff0c;仅从概念上对基于Python的图像形态学处理进行非常简要的介绍&#xff0c;不适合用于深入和详细的了解。 基于Python的图像形态学处理概述 Digital terrain models from airborne laser scanning for the automatic extra…
阅读更多...
蓝牙芯片PHY6222的一些基本信息

蓝牙芯片PHY6222的一些基本信息

摘要&#xff1a;本文简要介绍一下硬件工程师需要关注的PHY6222蓝牙芯片重点信息。 这个蓝牙芯片&#xff0c;支持蓝牙5.2. 内核是ARM Cortex™-M0 32-bit processor &#xff0c;这就证明它可以像开发STM32那样来为它开发程序。 具有SWD调试接口&#xff0c;那么就可以用少到…
阅读更多...
论文解读：Splicing ViT Features for Semantic Appearance Transfer

论文解读：Splicing ViT Features for Semantic Appearance Transfer

Project webpage: https://splice-vit.github.io Abstruct 将两张图片中语义相近的目标的结构和风格&#xff08;外观&#xff09;拼接 • 输入一个 Structure/ Appearence 图像对 &#xff1a; 训练生成器 。 • 关键思想是利用 预训练 和固定的视觉转换器 ( ViT ) 模型&…
阅读更多...
Smartbi内置用户登陆绕过漏洞复现

Smartbi内置用户登陆绕过漏洞复现

0x01 产品简介 Smartbi大数据分析产品融合BI定义的所有阶段&#xff0c;对接各种业务数据库、数据仓库和大数据分析平台&#xff0c;进行加工处理、分析挖掘和可视化展现&#xff1b;满足所有用户的各种数据分析应用需求&#xff0c;如大数据分析、可视化分析、探索式分析、复杂…
阅读更多...
Push vs Pull

Push vs Pull

Push好在两点&#xff1a;1.把结果下推到下流节点&#xff0c;与控制流解耦合&#xff0c;有利于cache 2.对于有向无环图&#xff0c;而不仅仅是树的query plan有更好的效果 解释&#xff1a; pull伪代码 push 伪代码 解释一下push&#xff0c;就是把操作下推到叶子节点&#…
阅读更多...
4-JVM类加载

4-JVM类加载

目录 1.类加载过程 1.1.加载&#xff08;去车站&#xff09; 1.2.验证&#xff08;过安检&#xff09; 1.3.准备&#xff08;候车&#xff09; 1.4.解析&#xff08;检票&#xff09; 1.5.初始化&#xff08;上车&#xff09; 2.双亲委派模型 2.1.什么是双亲委派模型&a…
阅读更多...
首次曝光！乔布斯这些从未公开的照片，揭露乔布斯的另一面

首次曝光！乔布斯这些从未公开的照片，揭露乔布斯的另一面

昨个&#xff0c;大神在群里分享了一本关于乔布斯的书籍。 这本书收录了他的照片、电子邮件、演讲稿和访谈&#xff0c;很多私人的邮件和访谈是第一次看到。 书中用乔布斯自己的视角&#xff0c;记录了他一生的轨迹&#xff0c;包括他的童年&#xff0c;创立、离开、重归苹果的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023