目录

一、运算公式

二、平面的法线向量

---

注：加粗体为向量

一、运算公式

1.若a//b，那么a=λb

   若a⊥b，那么a*b=0

2.若A(x1,y1,z1)，B(x2,y2,z2)

   中点坐标：AB中点M(x1+x2/2,y1+y2/2,z1+z2/2)

   两点间的距离和模的计算：|AB|=|AB|=√(x2-x1)^2+(y2-y1)^2+(z2-z1)^2

3.a*b=|a|*|b|cosθ

   a*a=|a|^2

4.向量叉乘

   a×b=c

   |c|=|a||b|sinθ

   c的方向：垂直于a、b所在平面

二、平面的点法式

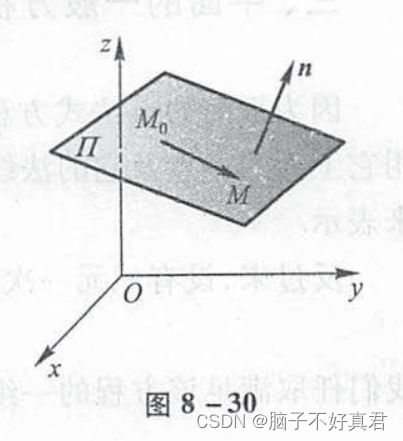
平面的点法式方程需要的量是平面内的一个向量MM0和平面的法线向量n。M0为已知点，M为假设的点。

若n=(A,B,C)，M0=(x0，y0，z0)，那么平面点法式方程为：

 2.平面的一般式

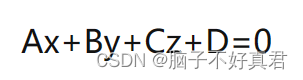
 平行于哪个轴，对应的A、B、C就为0。如果D=0，那么平面过原点。

例1：求平行于x0z面且经过点(2,-5,3)的平面方程。

例2：求过直线x-1/-1=y-1/0=z-1/-2并且垂直于平面x+y+z=0的平面方程。

直线过平面，则该直线上的每一个点都在此平面上，实际上计算该直线在平面上。

将(1,1,1)代入直线成立，说明(1,1,1)在直线上，也在平面上。

法向量垂直于该平面并且过一个点(我的理解)。

三、直线的点向式

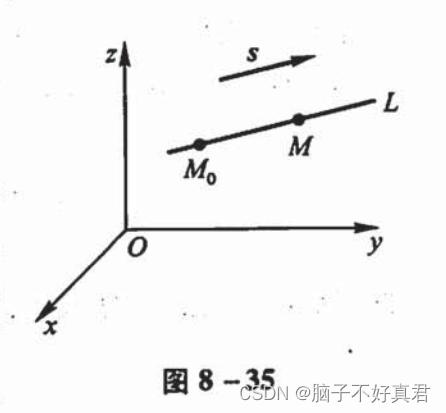
直线的点向式方程需要的量是直线上的两个点，M0、M为假设的点和方向向量。

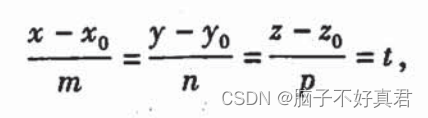
例1：求过点(1,-2,4)并且与平面2x-3y+z-4=0垂直的直线方程。

如图，s与n平行，所以s=λn，此时λ=1。

例2：求过点(0,2,4)并且与两平面x+2z=1和y-3z=2平行的直线方程。