Win10任务栏一直转圈圈不能操作怎么办?Win10电脑用户遇到了任务栏一直转圈圈不能操作的问题,不知道怎么操作才能解决,这时候用户可以打开桌面上的控制面板,点击卸载更新补丁,也可以通过打开命令提示符窗口,输入命令来解决此问题,解决后用户即可正常使用Win10任务栏。
解决办法:
方法一(前提桌面有控制面板)
1、打开桌面的控制面板,点击卸载程序。
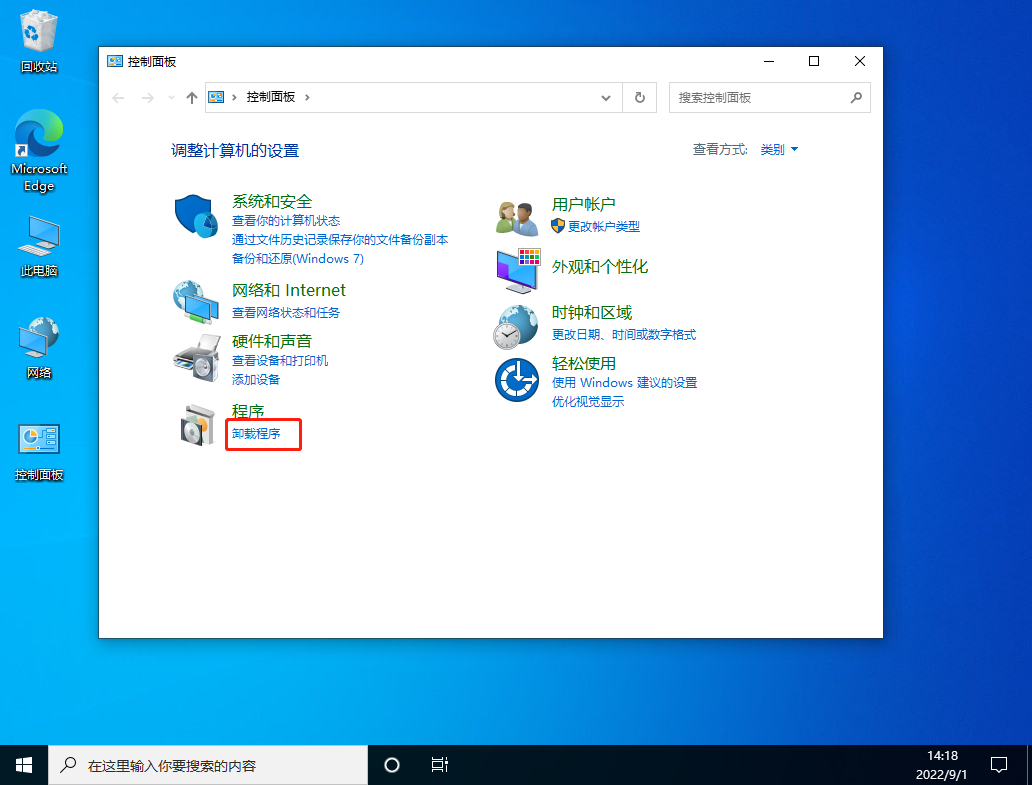
2、进入后,在左侧点击查看已安装的更新。
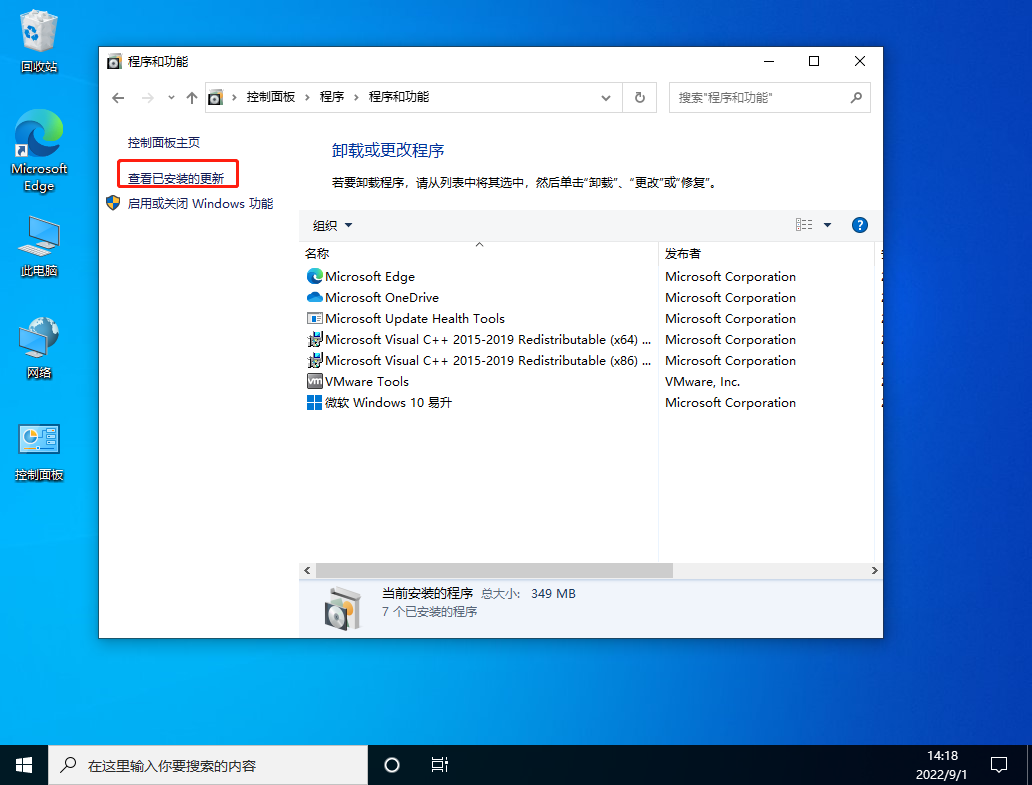
3、然后找到对应的KB5008212补丁,鼠标右键点击卸载即可。
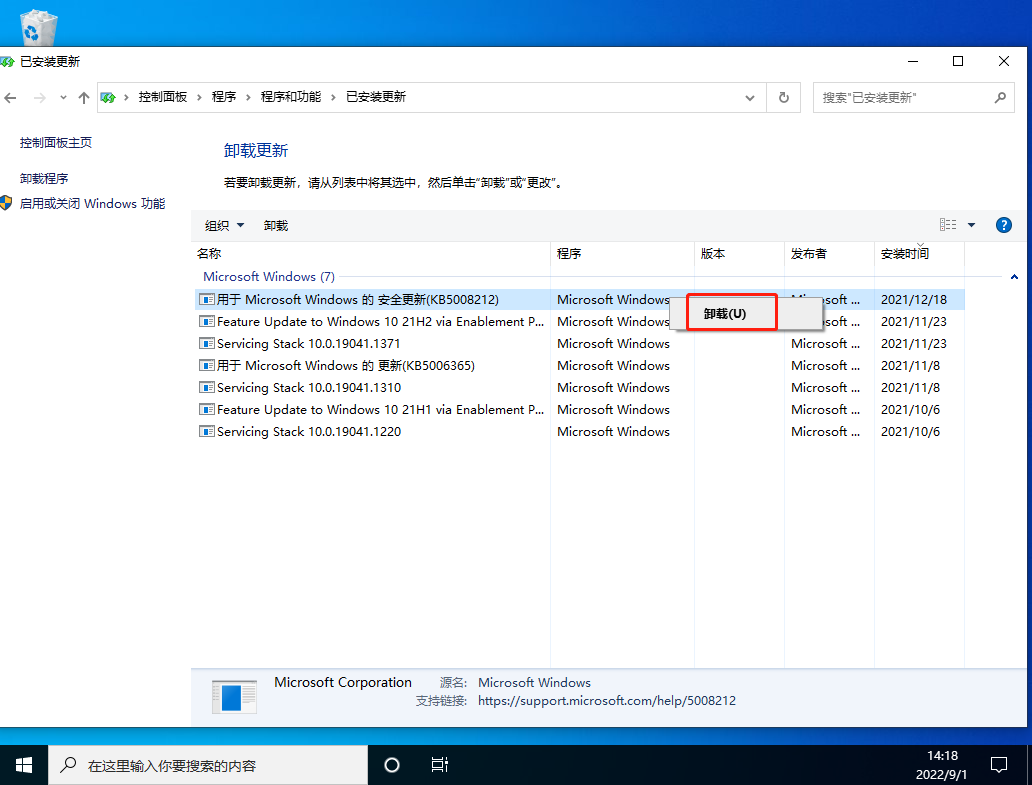
方法二
1、键盘按住Ctrl+shift+esc打开任务管理器。
2、在右上角点击文件,运行新任务。
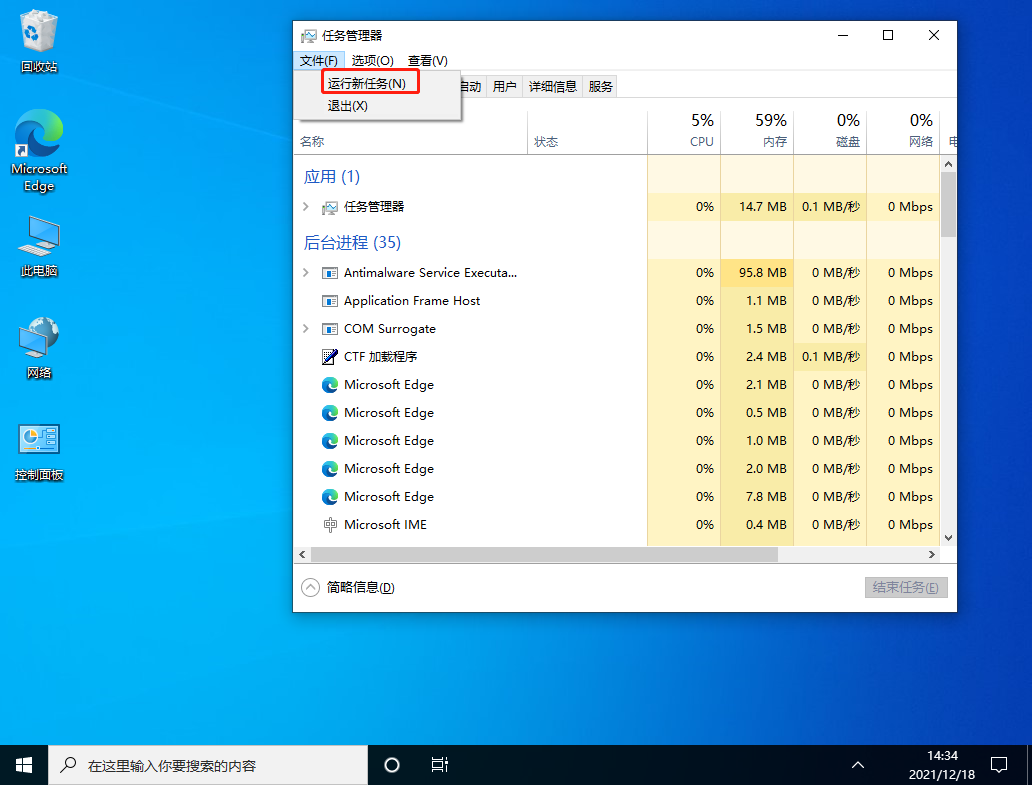
3、输入cmd,并且勾选以系统管理权限创建此任务。
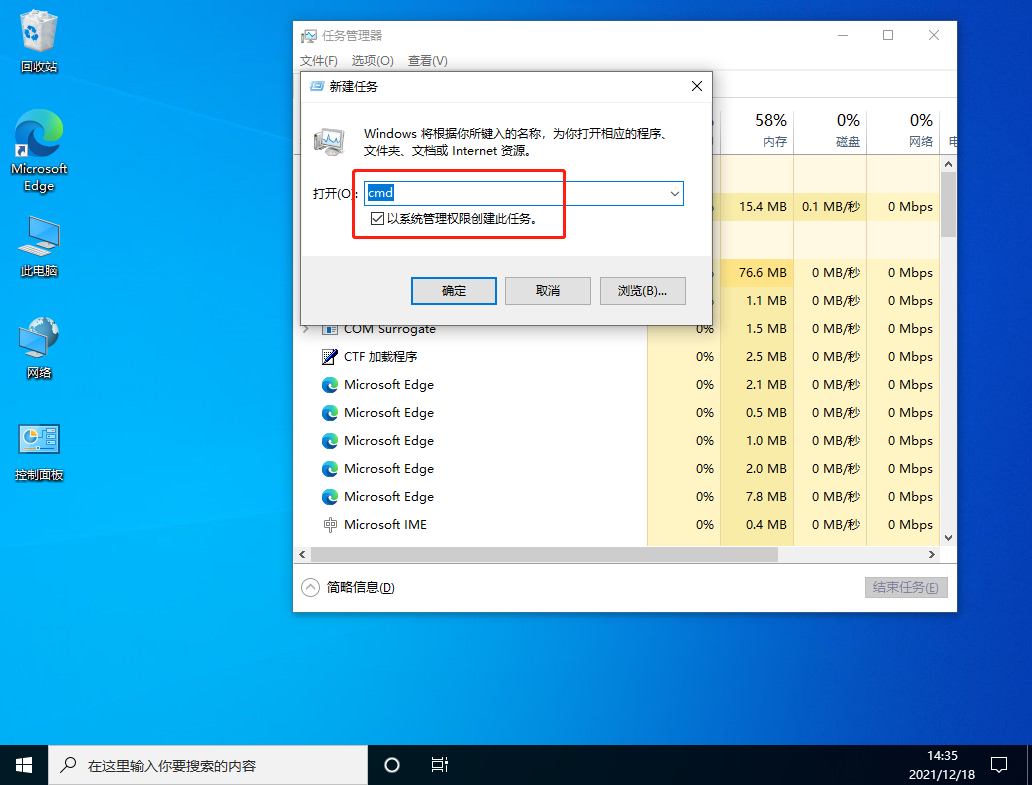
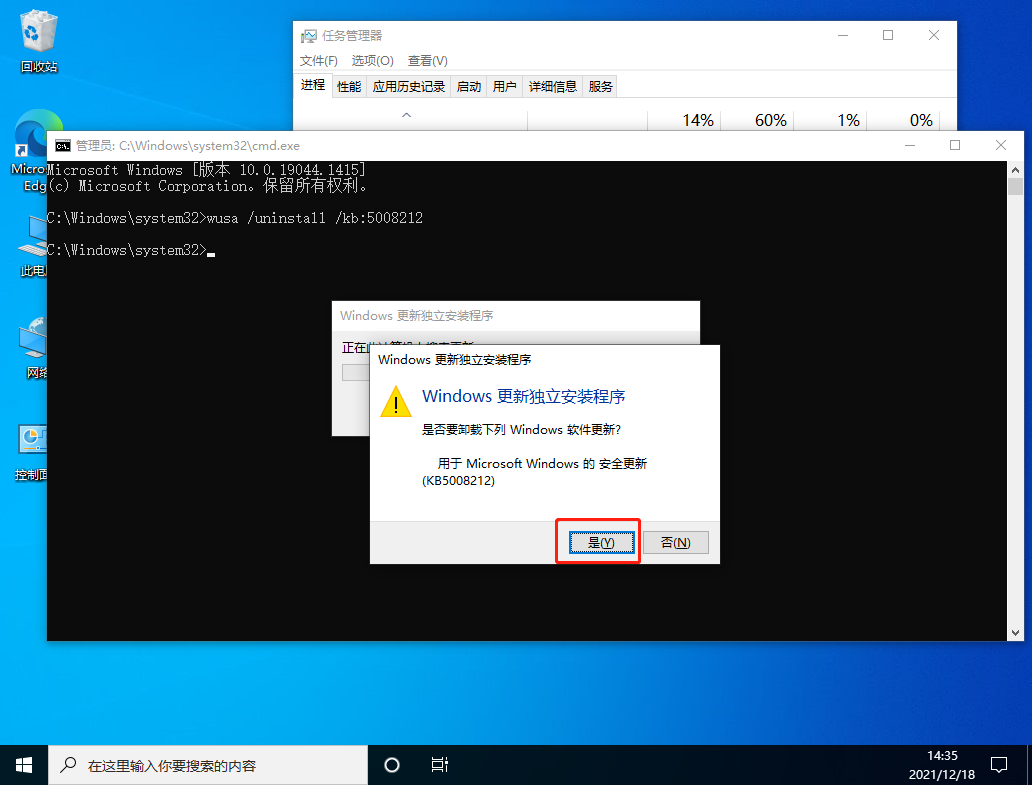
4、进入后,输入wusa /uninstall /kb:500821,在弹出的窗口选择是,等待卸载完成重启即可。
方法三
1、关闭无线网络和有线网络连接,让电脑处于断网状态。
2、重启电脑,进入系统。
3、断网后,系统任务栏设置等可以正常使用。
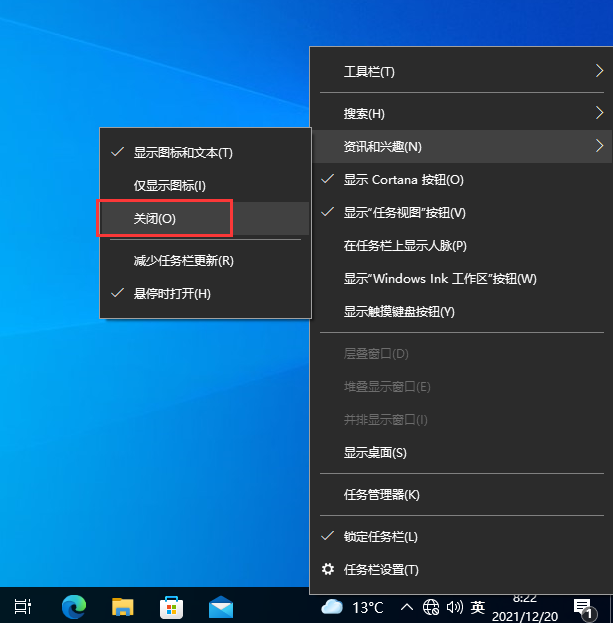
4、然后右键点击任务栏的空白处或资讯和兴趣上,选择关闭即可。







![强化学习从基础到进阶-常见问题和面试必知必答[1]:强化学习概述、序列决策、动作空间定义、策略价值函数、探索与利用、Gym强化学习实验](https://img-blog.csdnimg.cn/229b8254abd044448e19911f8255e473.png#pic_center)