引言

上一节介绍了对包含配分函数的概率分布——使用极大似然估计求解模型参数的梯度(对数似然梯度)，本节将基于上述结论，介绍随机最大似然(Stochastic Maximum Likelihood)。

回顾：对数似然梯度

已知样本集合 X = { x ( i ) } i = 1 N \mathcal X = \{x^{(i)}\}_{i=1}^N X={x(i)}i=1N​，且随机变量 X = { x 1 , ⋯   , x p } \mathcal X = \{x_1,\cdots,x_p\} X={x1​,⋯,xp​}在$p$维实数域上有意义($\mathcal{X}\in {\mathbb{R}}^p$)。
$\text{ML Learning : }$针对包含配分函数的概率模型$\mathcal{P}(\mathcal{X};\theta )$中对模型参数$\theta$进行求解。以极大似然估计为例，最优模型参数$\hat{\theta }$表示如下：
$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}\log \prod _{i=1}^N\mathcal{P}(x^{(i)};\theta )\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^N\log \left[\frac{1}{\mathcal{Z}(\theta )}\hat{\mathcal{P}}(x^{(i)};\theta )\right]\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^N\left[\log \hat{\mathcal{P}}(x^{(i)};\theta )-\log \mathcal{Z}(\theta )\right]\end{array}$$
其中$\hat{\mathcal{P}}(\mathcal{X};\theta )$表示不包含配分函数的概率模型结果；$\mathcal{Z}(\theta )$表示配分函数(Partition Function)，假设$\mathcal{X}$是连续型随机变量，配分函数可表示为：
$$\begin{array}{rl}\mathcal{Z}(\theta )& ={\int }_{\mathcal{X}}\hat{\mathcal{P}}(\mathcal{X};\theta )d\mathcal{X}\\ & ={\int }_{x_1},\cdots ,{\int }_{x_p}\hat{\mathcal{P}}(x_1,\cdots ,x_p;\theta )d(x_1,\cdots ,x_p)\end{array}$$
将上式进行整理，可表示为如下表达：
$$\{\begin{array}{l}\mathcal{L}(\theta )=\frac{1}{N}{\sum }_{i=1}^N\log \hat{\mathcal{P}}(x^{(i)};\theta )-\log \mathcal{Z}(\theta )\\ \\ \hat{\theta }=\underset{\theta }{\mathrm{argmax}}\mathcal{L}(\theta )\end{array}$$
针对最大值的求解，常用方法是梯度上升法。对目标函数$\mathcal{L}(\theta )$关于$\theta$求梯度：
$${\nabla }_{\theta }\mathcal{L}(\theta )=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )-{\nabla }_{\theta }\log \mathcal{Z}(\theta )$$
通常将$\frac{1}{N}{\sum }_{i=1}^N{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )$看作正相，将${\nabla }_{\theta }\log \mathcal{Z}(\theta )$看作负相。
针对负相计算中的难点，将$\mathcal{Z}(\theta )$展开，最终化为期望形式：
$${\nabla }_{\theta }\log \mathcal{Z}(\theta )={\mathbb{E}}_{\mathcal{P}(\mathcal{X};\theta )}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )\right]$$
最终目标函数梯度${\nabla }_{\theta }\mathcal{L}(\theta )$可表示为如下形式：
$${\nabla }_{\theta }\mathcal{L}(\theta )=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )-{\mathbb{E}}_{\mathcal{P}(\mathcal{X};\theta )}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )\right]$$
关于正相部分可以使用如基于$\text{Batch/mini-Batch}$的梯度上升方法(因为样本是给定的)；关于负相部分可以使用马尔可夫链蒙特卡洛方法进行近似求解。

关于${\nabla }_{\theta }\mathcal{L}(\theta )$的简化

为了将正相与负相的格式统一，也将正相写成期望形式，这里引入一个概率分布——真实分布${\mathcal{P}}_{data}$。

早在第一节极大似然估计与最大后验概率估计介绍过概率模型的概念。一个真实模型${\mathcal{P}}_{data}(\mathcal{X};\theta )$，可以通过模型参数$\theta$生成无穷无尽的样本，而我们的样本集合$\mathcal{X}$只是其中的一个 子集。由于噪声的原因，我们可能无法将真实模型的分布精确的求解出来，但可以通过样本集合$\mathcal{X}$对真实分布进行近似。样本量越多，样本分布结果越接近真实分布。
简单理解为，真实分布是基于问题客观存在的，但是它很‘缥缈’,我们只能得到它的近似结果。
通过已有样本集合$\mathcal{X}$估计出的‘近似分布’称为‘经验分布’(Empirical Distribution)。

但是在这里，虽然经验分布只是真实分布的一个近似，但是在这里将正相看作是基于真实分布的期望。因为正相确实是通过采样真实样本的方式更新梯度的。
相比之下，概率模型$\mathcal{P}(\mathcal{X};\theta )=\frac{1}{\mathcal{Z}(\theta )}\hat{\mathcal{P}}(\mathcal{X};\theta )$是基于概率图结构的假设。与${\mathcal{P}}_{data}$相对应，称其为${\mathcal{P}}_{model}$。

至此，关于${\nabla }_{\theta }\mathcal{L}(\theta )$的简化结果可表示为：
$$\begin{array}{rl}{\nabla }_{\theta }\mathcal{L}(\theta )& =\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )-{\mathbb{E}}_{\mathcal{P}(\mathcal{X};\theta )}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )\right]\\ & ={\mathbb{E}}_{{\mathcal{P}}_{data}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )]-{\mathbb{E}}_{{\mathcal{P}}_{model}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )]\end{array}$$

之所以称${\mathbb{E}}_{{\mathcal{P}}_{data}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )]$为正相，是因为 正向的增加了${\nabla }_{\theta }\mathcal{L}(\theta )$梯度上升的过程；相反，由于负相${\mathbb{E}}_{{\mathcal{P}}_{model}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )]$的增加使得${\nabla }_{\theta }\mathcal{L}(\theta )$梯度上升的过程放缓(起到反作用)。

基于MCMC求解负相

之前介绍过了，如果负相能够轻松地求解出结果，那么可以直接使用梯度上升法(Gradient Ascent)对模型参数$\theta$进行近似求解：
$\eta$表示学习率~
$${\theta }^{(t+1)}\Leftarrow {\theta }^{(t)}+\eta {\nabla }_{\theta }\mathcal{L}(\theta )$$
如果负相无法求解出精确结果，那么通常采用马尔可夫链蒙特卡洛方法,如吉布斯采样(Gibbs Sampling)进行求解。

而这个采样过程本质上是迭代过程。否则就是从分布${\mathcal{P}}_{model}=\mathcal{P}(\mathcal{X};\theta )$中进行采样，而$\theta$是我们要求解的量，两者之间相互矛盾。

如果想要求解$t+1$次迭代的负相，需要从上一迭代的分布${\mathcal{P}}_{model}=\mathcal{P}(\mathcal{X};{\theta }^{(t)})$中进行采样：
《深度学习》(花书)中称从${\mathcal{P}}_{model}$中采集的样本称为“幻想粒子”(Fantasy Particle)。因为模型本身是基于’概率图结构‘假设的，那么${\mathcal{P}}_{model}$自然不是真实的。对于它采集的样本不足够信任。
$${\hat{x}}^{(t+1)}=\{\begin{array}{l}{{\hat{x}}_{t+1}}^{(1)}\sim \mathcal{P}(\mathcal{X};{\theta }^{(t)})\\ {{\hat{x}}_{t+1}}^{(2)}\sim \mathcal{P}(\mathcal{X};{\theta }^{(t)})\\ ⋮\\ {{\hat{x}}_{t+1}}^{(\mathcal{M})}\sim \mathcal{P}(\mathcal{X};{\theta }^{(t)})\end{array}$$

至此，基于梯度上升法模型参数$\theta$的迭代过程归纳如下：
$${\theta }^{(t+1)}\Leftarrow {\theta }^{(t)}+\eta \left[\sum _{i=1}^{\mathcal{M}}{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};{\theta }^{(t)})-\sum _{i=1}^{\mathcal{M}}{\nabla }_{\theta }\log \hat{\mathcal{P}}({\hat{x}}^{(i)};{\theta }^{(t)})\right]$$
个人理解：

• 上面中括号中均少了$\frac{1}{\mathcal{M}}$应该是并在了$\eta$中;
• 这里仅是使用’吉布斯采样方法‘从平稳分布中采集若干样本，和吉布斯采样本身的迭代过程(在实现平稳分布过程中每一个step对个维度采样、固定)没有关联关系。

关于书中图像的解释

某一维随机变量的概率分布表示如下(蓝色线)：

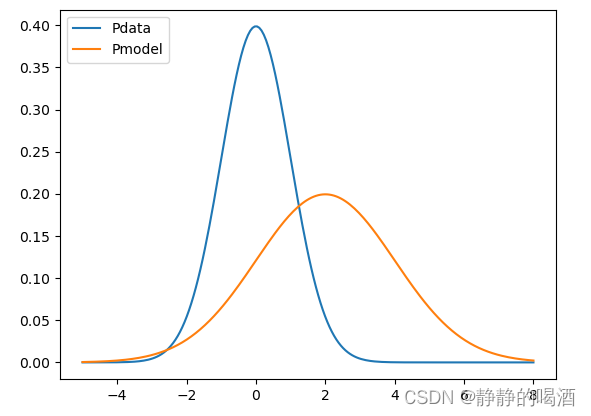
而橙色线表示假设的概率模型${\mathcal{P}}_{model}=\mathcal{P}(\mathcal{X};\theta )$在某迭代步骤的概率分布预测结果。

回顾梯度${\nabla }_{\theta }\mathcal{L}(\theta )$在梯度上升法的作用，我们希望每一次迭代，梯度结果越高，它的梯度方向就越指向最优模型参数：
$${\nabla }_{\theta }\mathcal{L}(\theta )=\underset{\text{Positive Phase}}{\underbrace{{\mathbb{E}}_{{\mathcal{P}}_{data}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )]}}-\underset{\text{Negative Phase}}{\underbrace{{\mathbb{E}}_{{\mathcal{P}}_{model}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )]}}$$
从而有：正相越高越好，负相越低越好。

• 首先，从${\mathcal{P}}_{data}$中采集了$\mathcal{M}$个样本，由于${\mathcal{P}}_{data}$的概率密度函数，采集的样本更多概率聚集在0附近。
  ${\mathcal{P}}_{data}$是真实分布，是基于问题客观存在的。

• 拿到样本之后，对当前迭代步骤的正相进行求解。但求解并不是最终目的，而是希望使用极大似然估计，找到一款参数，使得$\mathcal{L}(\theta )$达到最大。
  而$\mathcal{L}(\theta )$达到最大的目的是让假设概率模型的分布${\mathcal{P}}_{model}$接近真实分布${\mathcal{P}}_{data}$.

  观察上图0附近的关于${\mathcal{P}}_{model}$的概率分布结果，很显然并不在${\mathcal{P}}_{model}$的波峰位置，这说明 此时的${\mathcal{P}}_{model}$和真实分布${\mathcal{P}}_{data}$是有差距的。

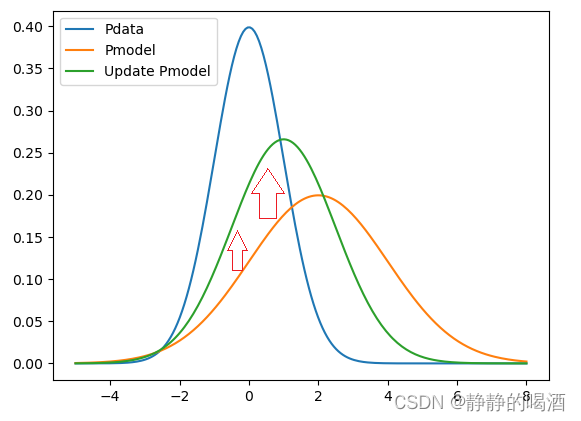
  如何缩小这种差距——通过修正模型参数$\theta$，让这些采集的样本对应的概率结果提高：
  此时${\mathcal{P}}_{model}$橙色线到绿色线的变化区域(横坐标)基本已经涵盖了${\mathcal{P}}_{data}$(蓝色线)的有效范围。在${\mathcal{P}}_{data}$有效范围内${\mathcal{P}}_{model}$的概率结果提高，从图形的趋势上来看，它相比之前的橙色线，更接近于${\mathcal{P}}_{data}$.
  图画的不好，见谅哈~
  

• 同理，观察负相，和正相不同的是，负相是从${\mathcal{P}}_{model}$中进行采样，而不是${\mathcal{P}}_{data}$。观察${\mathcal{P}}_{model}$的高概率部分(波峰部分)，与该部分样本点对应的${\mathcal{P}}_{data}$概率结果明显存在差距。
  如何缩小这种差距——调整模型参数$\theta$让这些采样点对应的概率结果降低。
  最终目标就是‘无限逼近’${\mathcal{P}}_{data}$。因为${\mathcal{P}}_{data}$是客观存在的，是恒定不变的。
  以正相结果为基础，进行如下修正：
  
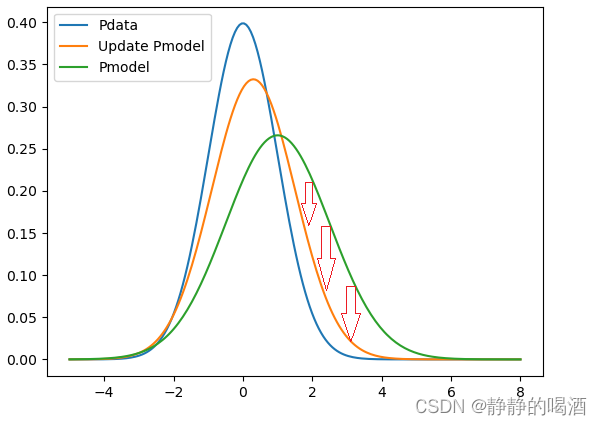
  相比于初始状态，此时已经很接近真实分布${\mathcal{P}}_{data}$了。
  需要注意的点：正相和负相不是各变各的，而是同时进行。

• 迭代过程到什么状态下停止？
  从${\nabla }_{\theta }\mathcal{L}(\theta )$中可以看出：
  $${\nabla }_{\theta }\mathcal{L}(\theta )=\underset{\text{Positive Phase}}{\underbrace{{\mathbb{E}}_{{\mathcal{P}}_{data}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )]}}-\underset{\text{Negative Phase}}{\underbrace{{\mathbb{E}}_{{\mathcal{P}}_{model}}[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )]}}$$
  正相、负相期望中的函数部分完全相同，只有期望基于的概率分布(${\mathcal{P}}_{model},{\mathcal{P}}_{data}$)不一样。如果${\mathcal{P}}_{model}={\mathcal{P}}_{data}$，${\nabla }_{\theta }\mathcal{L}(\theta )=0$，不会再更新梯度，此时迭代过程自然就停止了。

下一节将介绍对比散度。
相关参考：
直面配分函数-2-Stochastic Maximum Likelihood(随机最大似然)
深度学习(花书)——第18章 直面配分函数