基于非局部滤波图像去噪方法

news2024/10/7 14:21:53

论文题目：A non-local algorithm for image denoising

`1 摘要`

我们提出了一种新的衡量噪声的方法，来评价和比较数字图像去噪方法的性能。我们首先计算和分析该方法的噪声类去噪算法，即局部平滑滤波器。其次，我们提出了一种新的算法非局部均值（NL-means），基于图像中所有像素的非局部平均。最后，我们比较了nl-均值算法和局部平滑滤波器的实验。

`2 理论介绍`

`2.1 背景`

图像中的像素不是孤立存在的，它们高度相关，其像素不仅相似，而且与周围的像素一起形成图像的几何结构，即具有几何相似性。邻域像素中心窗口或图像patch，可以反映像素的结构特征，如循环模式和纹理结构。因此，在整个图像补丁中有很多相似的结构，如果使用可以描述图像结构特征来衡量像素之间的相似性，将比单像素更准确，从而更好地保护图像的结构信息。
并提出并分析了由简单公式定义的NL-means算法：
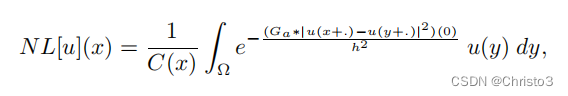
在这里插入图片描述

在这里插入图片描述

下图是 $N L - m e a n s$ 算法执行过程，大窗口是以目标像素为中心的搜索窗口，两个灰色小窗口分别是以 $x$ 、 $y$ 中心的邻域窗口。其中以 $y$ 为中心的邻域窗口在搜索窗口中滑动，通过计算两个邻域窗口间的相似程度为 $y$ 赋以权值 $w (x, y)$ 。

在这里插入图片描述

`2.2 非局部均值方法`

给定一个离散的噪声图像 $v = {v (i) | i∈I}$ ，对于一个像素 $i$ 的估计值 $N L [v] (i)$ 被计算为图像中所有像素的加权平均值，
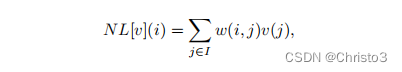
在这里插入图片描述
其中，权值族 ${w(i，j)}_j$ 依赖于像素 $i$ 和 $j$ 之间的相似性，并满足通常的条件 $0 \leq w (i, j) \leq 1$ 和 $\sum_j w(i,j)=1$ 。
两个像素 $i$ 和 $j$ 之间的相似性取决于强度灰度级向量 $v(N_i)$ 和 $v(N_j)$ 的相似性，其中 $N_k$ 表示一个固定大小且以像素 $k$ 为中心的正方形邻域。相似度衡量作为加权欧几里得距离的递减函数， $v(N_i)−v(N_j)||_2^2,a$ ，其中 $a > 0$ 是高斯核的标准差。将欧几里得距离应用于噪声邻域，提出了以下等式:
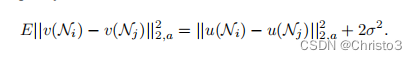
在这里插入图片描述
这个等式表明了该算法的鲁棒性，因为在期望中，欧氏距离保持了像素之间的相似性的顺序。
与 $v(N_i)$ 灰度邻域相似的像素在平均值中具有较大的权重，见图1。这些权重被定义为：

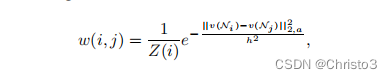
其中 $Z (i)$ 是归一化常数
在这里插入图片描述
而参数 $h$ 作为一个滤波的程度。它控制了指数函数的衰减，因此也控制了权值作为欧几里得距离的函数的衰减。 $N L - m e a n$ 不仅比较单个点的灰度，而且比较整个邻域的几何结构。这一事实允许比邻域滤波器进行更稳健的比较。图1说明了这一事实，像素 $q 3$ 具有相同的灰度值像素 $p$ ，但邻域有很大的不同，因此权重 $w (p ， q 3)$ 接近于零。
在这里插入图片描述

`3 结论`

在这里插入图片描述
在本节中，我们比较了局部平滑滤波器和 $N L - m e a n s$ 算法在三个定义良好的标准下：方法噪声、恢复图像的视觉质量和均方误差，即恢复图像和真实图像之间的欧氏差。为了 $N L - m e a n s$ 算法的计算目的，我们可以在一个更大的 $S \times S$ 像素大小的“搜索窗口”中限制类似窗口的搜索。在所有的实验中，我们固定了一个 $21 \times 21$ 像素的搜索窗口和一个 $7 \times 7$ 像素的相似平方邻域 $N_i$ 。如果 $N^2$ 是图像的像素数，则算法的最终复杂度约为 $49 \times 441 \times N 2$ 。
$7 \times 7$ 相似窗口已经被证明足够大，可以对噪声鲁棒，足够小，可以处理细节和精细结构。当加入标准偏差 $σ$ 的噪声时，滤波参数 $h$ 被固定为 $10 * σ$ 。由于指数核的快速衰减，较大的欧几里得距离导致接近于零的权重作为一个自动阈值，见图2。
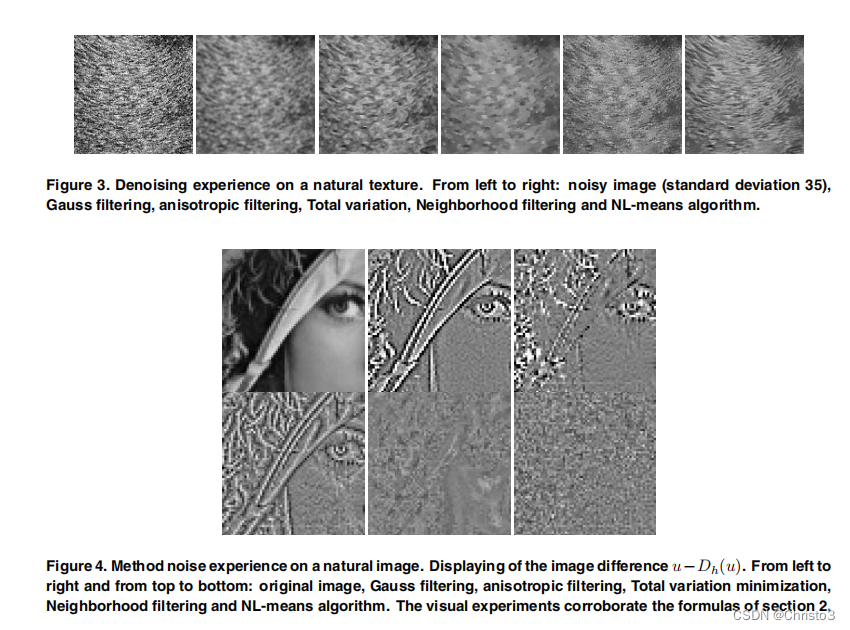
在第2节中，我们已经明确地计算了局部平滑滤波器的方法噪声。这些公式被图4的可视化实验验证了。该图显示了标准图像Lena的方法噪声，即差值 $u−D_h (u)$ ，其中参数 $h$ 被固定，以消除标准偏差为2.5的噪声。该方法噪声有助于我们理解去噪算法的性能和局限性，因为去除的细节或纹理具有很大的方法噪声。我们在图4中可以看到， $N L - m e a n s$ 方法的噪声没有呈现出任何明显的几何结构。图2解释了这个属性，因为它显示了 $N L - m e a n s$ 算法如何选择一个适应于图像的局部和非局部几何形状的加权配置。
在这里插入图片描述

人眼是唯一能够决定通过去噪方法是否提高了图像质量的方法。我们展示了一些去噪经验，比较了与局部平滑滤波器的去噪算法。所有实验都通过在真实图像中加入标准差 $σ$ 的高斯白噪声进行模拟。目的是比较恢复后的图像的视觉质量，伪影的不存在和边缘、纹理和细节的正确重建。
由于算法的性质， $N L - m e a n s$ 最有利的情况是纹理或周期情况。在这种情况下，对于每个像素 $i$ ，我们都可以找到具有非常相似配置的大量样本集。参见图2 e)的一个周期图像的 $N L - m e a n s$ 算法的权重分布示例。图3比较了一个自然纹理的NL-means和局部平滑滤波器的性能。
自然图像也有足够的冗余度，可以通过NL-means进行恢复。平面区域在同一对象内部呈现了大量类似的配置，见图2 (a).直线或弯曲的边有一条具有相似配置的完整像素线，见图2 (b)和©.此外，自然图像允许我们在遥远的像素中找到许多类似的配置，如图2 (f)所示。图5显示了一个关于自然图像的实验。这个经验必须与图4进行比较，在图4中，我们显示了原始图像的方法噪声。恢复图像的模糊或退化结构与方法噪声的明显结构相一致。