高斯过程指的是一组随机变量的集合,这个集合里面的任意有限个随机变量都服从联合正态分布。(联合正态分布是指多个随机变量的联合分布满足正态分布。联合分布是指多个随机变量同时满足的概率分布,一个常见的例子是考虑两个随机变量:X 表示一个人的年龄,Y 表示他们的身高。假设 X 和 Y 的联合分布是正态分布。在这种情况下,联合分布可以描述不同年龄的人在不同身高下出现的概率。我们可以使用联合概率密度函数来计算某个年龄范围内的人在某个身高范围内出现的概率。)
高斯过程可以用于回归拟合。先来看一个简单的例子。一个地点的气温,我们有过去10年6月1号的气温数据,想要预测明年6月1日的气温,那么假定那一天的气温服从高斯分布,根据过去的数据,可以算出均值和方差
,则明年那一天的气温
满足这样一个正态分布,最有可能的气温就是均值
。
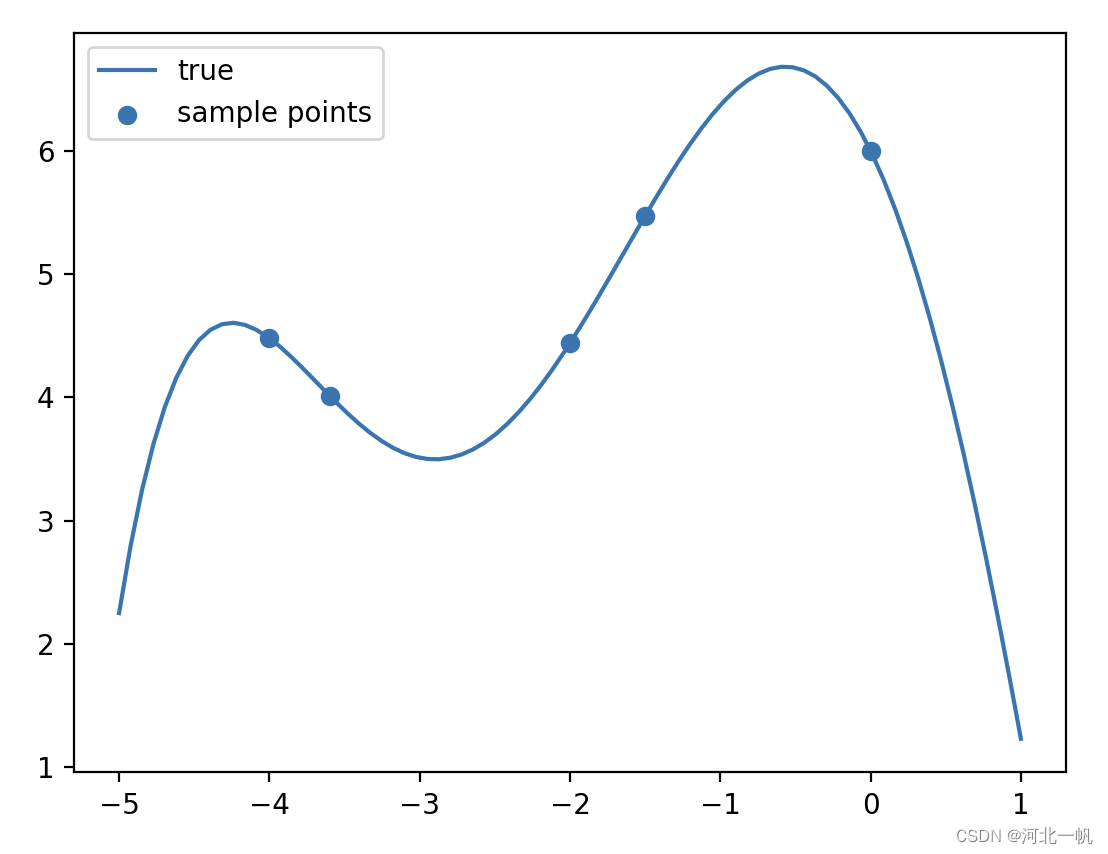
那么如果是一个一元5次函数比如
画出图像和几个已知点
import numpy as np
import matplotlib.pyplot as plt
def f(x):
coefs = [6, -2.5, -2.4, -0.1, 0.2, 0.03]
total = 0
for exp, coef in enumerate(coefs):
total += coef * (x ** exp)
return total
x_obs = np.array([-4, -3.6, -2.0, -1.5, 0])
y_obs = f(x_obs)
x_s = np.linspace(-5, 1, 80)
fig, ax = plt.subplots()
legend_list = []
ax.plot(x_s, f(x_s))
legend_list.append("true")
ax.scatter(x_obs, y_obs)
legend_list.append("sample points")
plt.legend(legend_list)
plt.show()
在已知几个点的情况下,如何通过高斯过程回归预测这个函数呢?
首先回顾一下高斯概率分布,一维高斯分布概率密度函数。
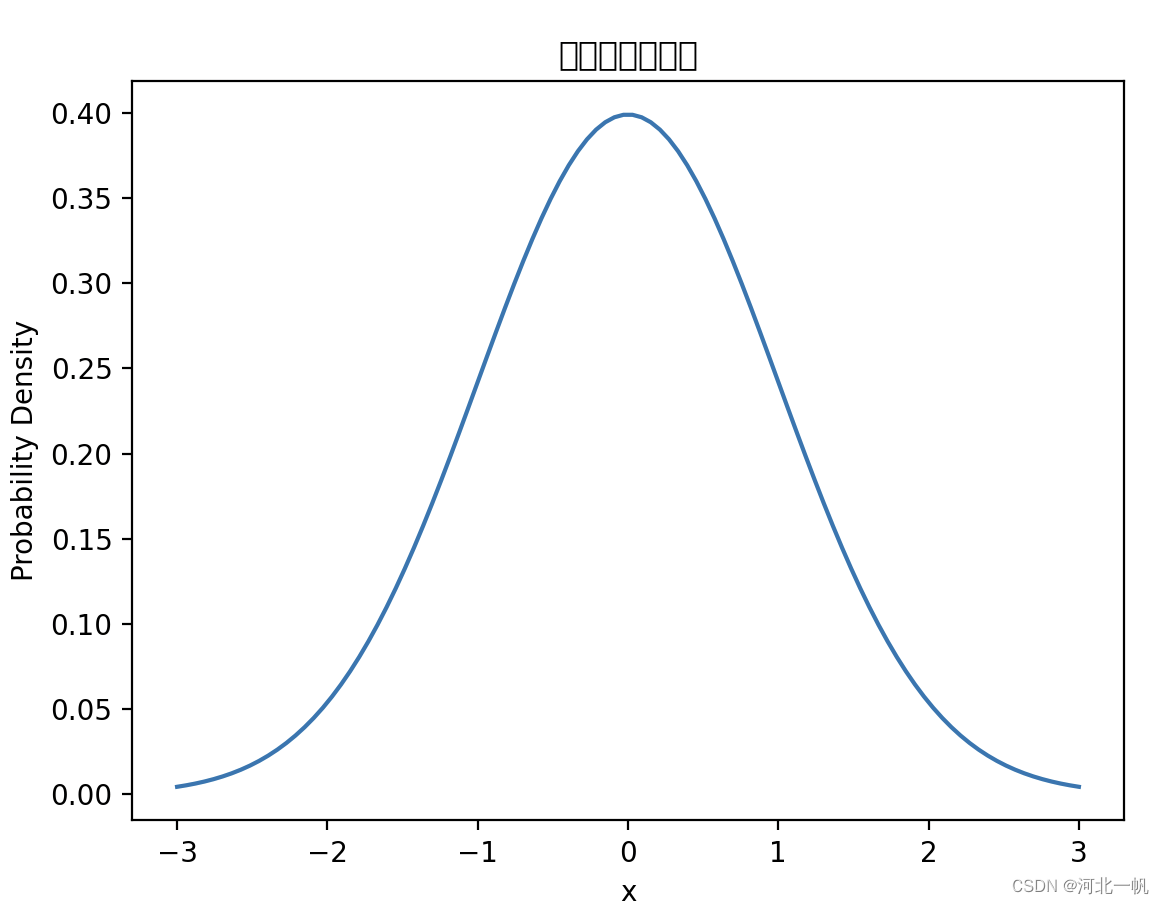
x有95%的可能性出现在95%置信区间[-1.96, 1.96]。调整均值和方差,96%置信区间就会移动。
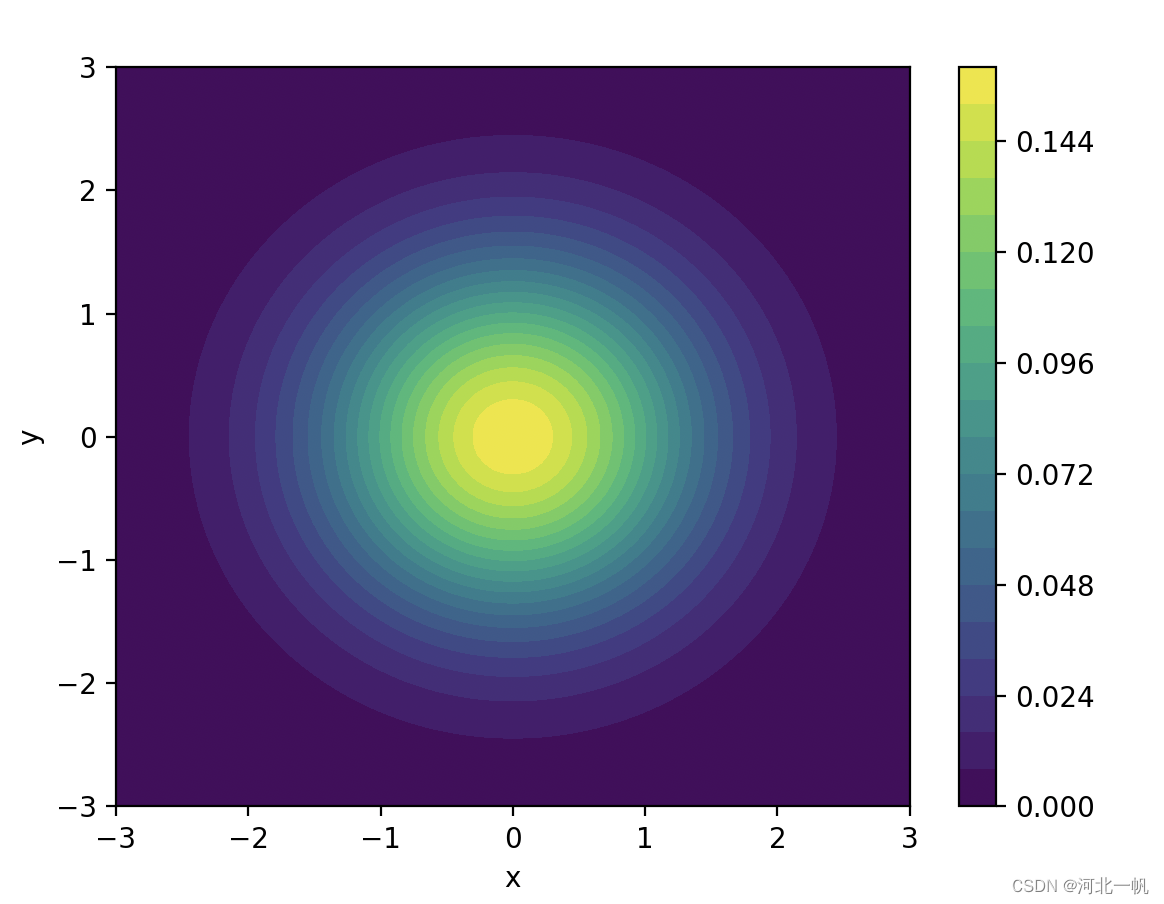
如果是二维高斯分布概率密度函数,下图。
代码如下
import numpy as np
import matplotlib.pyplot as plt
# 设置均值和协方差矩阵
mu = np.array([0, 0]) # 均值
cov = np.array([[1, 0], [0, 1]]) # 协方差矩阵
# 生成二维高斯分布的概率密度函数
x, y = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100))
pos = np.dstack((x, y))
inv_cov = np.linalg.inv(cov)
pdf = np.exp(-0.5 * np.einsum('...k,kl,...l->...', pos - mu, inv_cov, pos - mu)) / (2 * np.pi * np.sqrt(np.linalg.det(cov)))
# 绘制二维高斯分布图
plt.contourf(x, y, pdf, levels=20) # 使用contourf函数填充等高线图
plt.colorbar() # 添加颜色条
# 设置图形标题和轴标签
plt.xlabel('x')
plt.ylabel('y')
# 显示图形
plt.show()
那么我们进行一次采样,得到的点大概率是出现在黄色区域,如果我们把这个点表示为,y1,y2分别表示横纵坐标。通过调整协方差矩阵,黄色区域就会移动,我们就能得到不同的y。
如果是n维高斯分布,取样一次得到1个点的n个维度值。由此可以联想到,是否可以通过对n维高斯分布进行一次取样,来得到前文中那个5次函数的回归预测值呢?当然是可以的。
现在有一系列的x值
x_s = np.linspace(-5, 1, 80)通过对高维高斯分布进行一次取样,可以得到一系列y_s,从x_s映射到y_s的关键就在于协方差矩阵,通过核函数,可以构造不同的协方差矩阵。这里我们选择最简单的核函数。
import numpy as np
def k(xs, ys, sigma=1, l=1):
dx = np.expand_dims(xs, 1) - np.expand_dims(ys, 0)
tmp = (sigma ** 2) * np.exp(-((dx / l) ** 2) / 2)
return tmp
x_s = np.linspace(-5, 1, 80)
kernal = k(x_s, x_s)
预备知识告一段落,下面来看高斯过程回归是如何实现的:
先说明字母含义,x和y是我们已知的采样点,对应代码x_obs, y_obs。
x_obs = np.array([-4, -3.6, -2.0, -1.5, 0])
y_obs = f(x_obs)对应我们代码的x_s,
对应代码y_s。m(x)表示求均值,K是核函数运算得到的矩阵。
高斯过程回归的原理是:与
的联合概率分布(先验分布)符合高斯分布。
通过采样得到观测值y_obs以后,则的后验分布满足均值为
,方差为
的高斯分布:
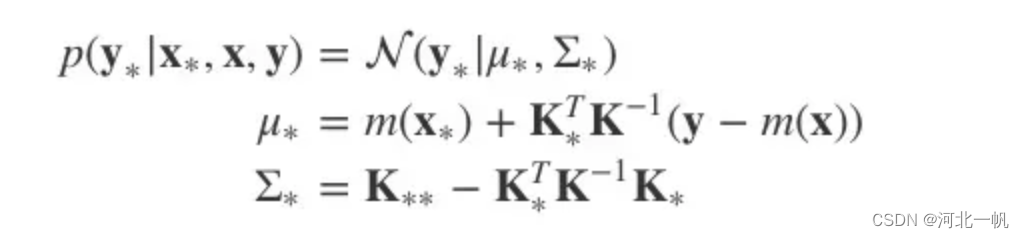
m和K的求法:
K = k(x_obs, x_obs)
K_s = k(x_obs, x_s)
K_ss = k(x_s, x_s)
K_sTKinv = np.matmul(K_s.T, np.linalg.pinv(K))
mu_s = m(x_s) + np.matmul(K_sTKinv, y_obs - m(x_obs))
Sigma_s = K_ss - np.matmul(K_sTKinv, K_s)高斯过程回归结果如下图
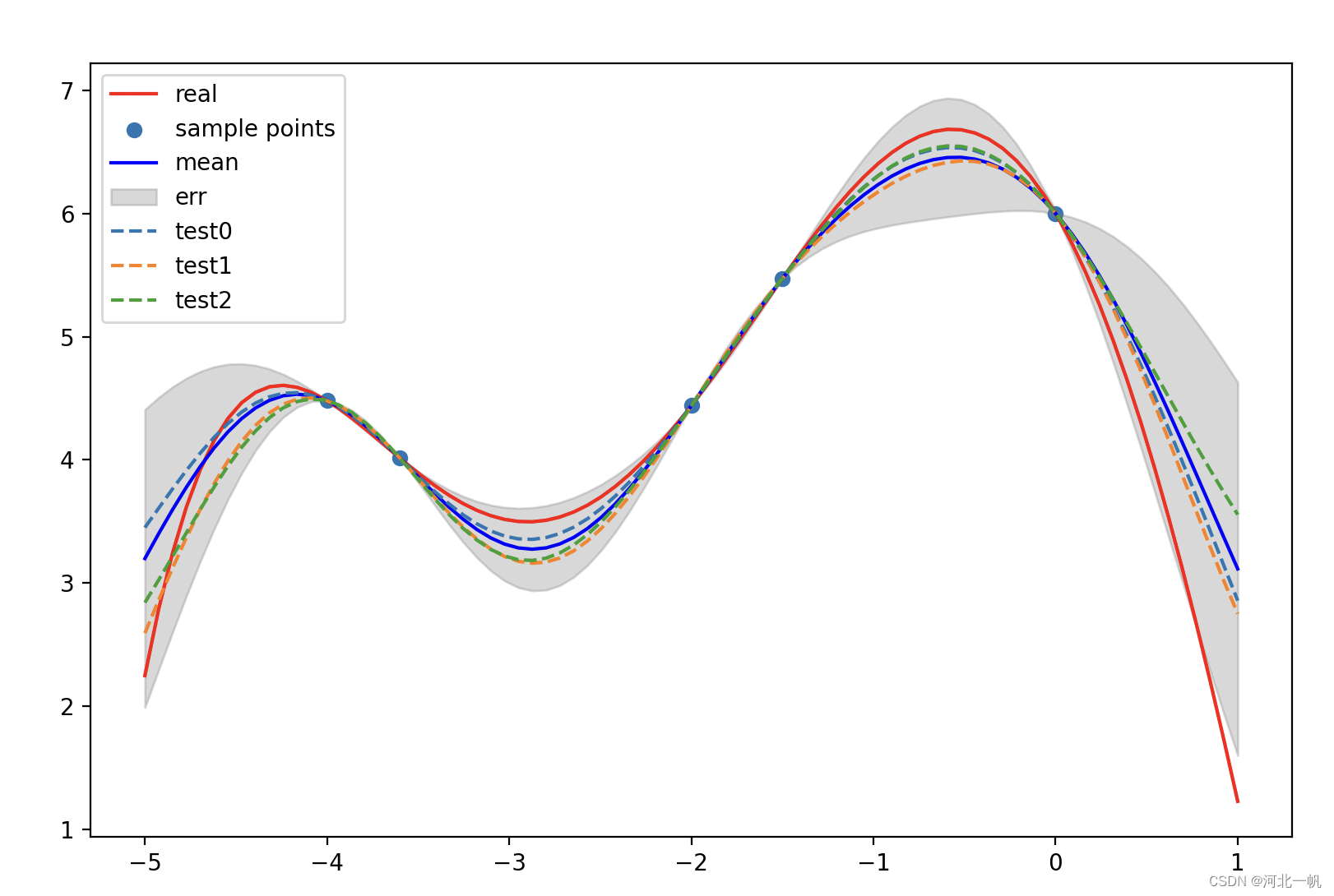
解释一下这张图,红色实线是函数真实值,蓝色实线是高斯过程回归的结果。三根虚线表示:对80维高斯分布(因为我们的x_s是80维数组)进行三次采样,得到的3个点,每个点80个维度坐标值组成的曲线。每个维度上的值,都是满足均值为蓝色实线,方差为灰色背景范围的高斯分布。在已知观测点上,方差为0,而距离观测点越远,方差范围越大,可信度也就越低。
完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
coefs = [6, -2.5, -2.4, -0.1, 0.2, 0.03]
total = 0
for exp, coef in enumerate(coefs):
total += coef * (x ** exp)
return total
def m(x):
tmp = np.zeros_like(x)
return tmp
def k(xs, ys, sigma=1, l=1):
dx = np.expand_dims(xs, 1) - np.expand_dims(ys, 0)
tmp = (sigma ** 2) * np.exp(-((dx / l) ** 2) / 2)
return tmp
x_obs = np.array([-4, -3.6, -2.0, -1.5, 0])
y_obs = f(x_obs)
x_s = np.linspace(-5, 1, 80)
K = k(x_obs, x_obs)
K_s = k(x_obs, x_s)
K_ss = k(x_s, x_s)
K_sTKinv = np.matmul(K_s.T, np.linalg.pinv(K))
mu_s = m(x_s) + np.matmul(K_sTKinv, y_obs - m(x_obs))
Sigma_s = K_ss - np.matmul(K_sTKinv, K_s)
stds = np.sqrt(Sigma_s.diagonal())
tmp = np.flip(x_s, 0)
err_xs = np.concatenate((x_s, np.flip(x_s, 0)))
err_ys = np.concatenate((mu_s + 2 * stds, np.flip(mu_s - 2 * stds, 0)))
fig, ax = plt.subplots()
legend_list = []
ax.plot(x_s, f(x_s), color='r')
legend_list.append("real")
ax.scatter(x_obs, y_obs)
legend_list.append("sample points")
ax.plot(x_s, mu_s, color='b')
legend_list.append("mean")
ax.fill_between(x_s, mu_s-2*stds, mu_s+2*stds, alpha=0.3, color='gray')
legend_list.append("err")
for i in range(3):
ax.plot(x_s, np.random.multivariate_normal(mu_s, Sigma_s), linestyle='--')
legend_list.append("test" + str(i))
plt.legend(legend_list)
plt.show()