小波变换之pycwt
PyCWT是用于连续小波谱分析的Python模块,它包括小波变换和FFT算法统计分析的常规操作的集合。此外,该模块还包括交叉小波变换、小波相干性测试和样例脚本。
该模块需要NumPy和SciPy,matplotlib模块。
pip安装:
pip install pycwt
conda安装:
conda install -c conda-forge/label/gcc7 pycwt
示例
基于小波的时间谱分析 Time-series spectral analysis using wavelets
在本例中,我们将采用Torrence和Compo(1998)[1]提出的方法,使用1871年至1996年的NINO3海面温度异常数据集。
[1] Torrence, C. and Compo, G. P… A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, American Meteorological Society, 1998, 79, 61-78. DOI.
我们从导入相关库开始。请确保PyCWT已正确安装在您的系统中。
from __future__ import division
import numpy
from matplotlib import pyplot
import pycwt as wavelet
from pycwt.helpers import find
注意:
from _ _ future _ _ import division必须在文件导包的第一行,即:
# -*- coding: utf-8 -*-
from __future__ import division
否则会出现如下错误:

然后,我们加载数据集并定义一些与数据相关的参数。在这种情况下,数据文件的前19行包含我们忽略的元数据,因为我们需手动设置它们(即标题,单位)。
url = 'http://paos.colorado.edu/research/wavelets/wave_idl/nino3sst.txt'
dat = numpy.genfromtxt(url, skip_header=19)
title = 'NINO3 Sea Surface Temperature'
label = 'NINO3 SST'
units = 'degC'
t0 = 1871.0
dt = 0.25 # In years
我们还创建了一个以年为单位的时间数组:
N = dat.size
t = numpy.arange(0, N) * dt + t0
接下来,通过标准差对输入数据进行去趋势化和标准化。有时不需要去趋势化,简单地去掉平均值就足够了。但是,如果您的数据集具有明确的趋势,例如上述网站上提供的莫纳罗亚 CO2 数据集,则强烈建议去趋势。在这里,我们拟合一个一次多项式函数,然后从原始数据中减去它。
p = numpy.polyfit(t - t0, dat, 1)
dat_notrend = dat - numpy.polyval(p, t - t0)
std = dat_notrend.std() # Standard deviation
var = std ** 2 # Variance
dat_norm = dat_notrend / std # Normalized dataset
原始数据dat长这样:
去趋势后dat_notrend:黄色线
标准化后dat_norm:
肉眼好像没看出啥太大区别。。。
下一步是定义小波分析的一些参数。我们选择了morlet母小波,在本例中是ω0=6的Morlet小波。
mother = wavelet.Morlet(6)
s0 = 2 * dt # Starting scale, in this case 2 * 0.25 years = 6 months
dj = 1 / 12 # Twelve sub-octaves per octaves
J = 7 / dj # Seven powers of two with dj sub-octaves
alpha, _, _ = wavelet.ar1(dat) # Lag-1 autocorrelation for red noise
下面的例程使用上面定义的参数执行小波变换和逆小波变换。由于我们对输入时间序列进行了归一化,我们将逆变换乘以标准差。
wave, scales, freqs, coi, fft, fftfreqs = wavelet.cwt(dat_norm, dt, dj, s0, J, mother)
iwave = wavelet.icwt(wave, scales, dt, dj, mother) * std
我们计算了归一化小波和傅立叶功率谱,以及每个小波尺度的傅立叶等效周期。
power = (numpy.abs(wave)) ** 2
fft_power = numpy.abs(fft) ** 2
period = 1 / freqs
我们也可以根据Liu等人(2007)提出的建议对功率谱进行校正。[2]
[2] Liu, Y., Liang, X. S. and Weisberg, R. H. Rectification of the bias in the wavelet power spectrum. Journal of Atmospheric and Oceanic Technology, 2007, 24, 2093-2102. DOI.
power /= scales[:, None]
我们可以在这里停下来,画出结果。当比值power / sig95 > 1时,功率是显著的。

画出power:
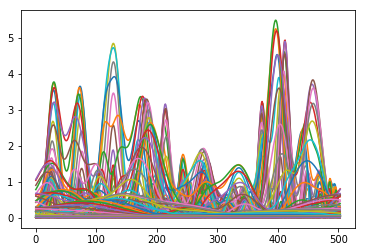
signif, fft_theor = wavelet.significance(1.0, dt, scales, 0, alpha,
significance_level=0.95,
wavelet=mother)
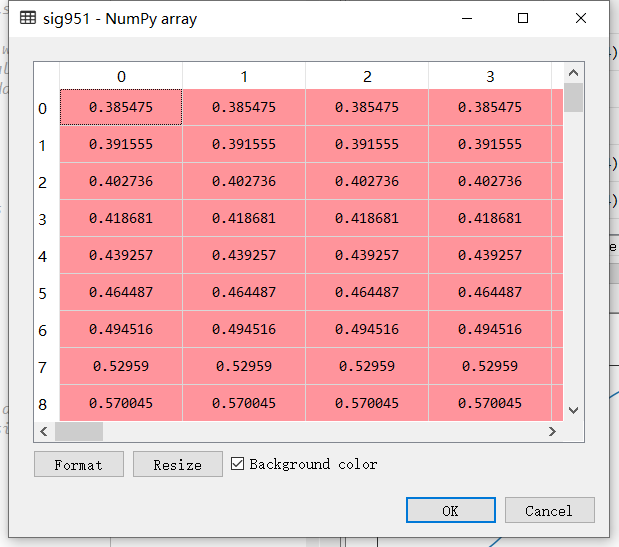
sig951 = numpy.ones([1, N]) * signif[:, None]
sig95 = power / sig951

画出sig95看看:
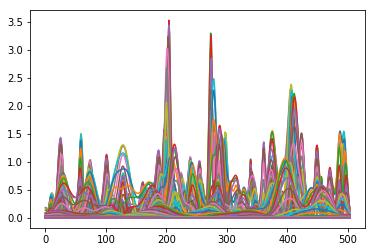
sig951的85个尺度上,每个尺度的值都是一样的。
画出来如下:
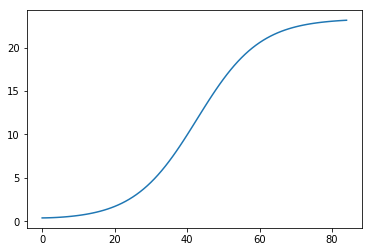
然后计算全局小波谱并确定其显著性水平。
glbl_power = power.mean(axis=1)
dof = N - scales # Correction for padding at edges
glbl_signif, tmp = wavelet.significance(var, dt, scales, 1, alpha,
significance_level=0.95, dof=dof,
wavelet=mother)
并计算了2 ~ 8年的量表平均值及其显著性水平。
sel = find((period >= 2) & (period < 8))
Cdelta = mother.cdelta
scale_avg = (scales * numpy.ones((N, 1))).transpose()
scale_avg = power / scale_avg # As in Torrence and Compo (1998) equation 24
scale_avg = var * dj * dt / Cdelta * scale_avg[sel, :].sum(axis=0)
scale_avg_signif, tmp = wavelet.significance(var, dt, scales, 2, alpha,
significance_level=0.95,
dof=[scales[sel[0]],
scales[sel[-1]]],
wavelet=mother)
最后,我们将结果绘制成包含(i)原始序列异常和逆小波变换的四个不同子图;(ii)小波功率谱(iii)全局小波和傅立叶谱;(iv)范围平均小波谱。在所有子图中,显著性水平要么包含为虚线,要么包含为填充等高线。
# Prepare the figure
pyplot.close('all')
pyplot.ioff()
figprops = dict(figsize=(11, 8), dpi=72)
fig = pyplot.figure(**figprops)
# First sub-plot, the original time series anomaly and inverse wavelet
# transform.
ax = pyplot.axes([0.1, 0.75, 0.65, 0.2])
ax.plot(t, iwave, '-', linewidth=1, color=[0.5, 0.5, 0.5])
ax.plot(t, dat, 'k', linewidth=1.5)
ax.set_title('a) {}'.format(title))
ax.set_ylabel(r'{} [{}]'.format(label, units))
# Second sub-plot, the normalized wavelet power spectrum and significance
# level contour lines and cone of influece hatched area. Note that period
# scale is logarithmic.
bx = pyplot.axes([0.1, 0.37, 0.65, 0.28], sharex=ax)
levels = [0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16]
bx.contourf(t, numpy.log2(period), numpy.log2(power), numpy.log2(levels),
extend='both', cmap=pyplot.cm.viridis)
extent = [t.min(), t.max(), 0, max(period)]
bx.contour(t, numpy.log2(period), sig95, [-99, 1], colors='k', linewidths=2,
extent=extent)
bx.fill(numpy.concatenate([t, t[-1:] + dt, t[-1:] + dt,
t[:1] - dt, t[:1] - dt]),
numpy.concatenate([numpy.log2(coi), [1e-9], numpy.log2(period[-1:]),
numpy.log2(period[-1:]), [1e-9]]),
'k', alpha=0.3, hatch='x')
bx.set_title('b) {} Wavelet Power Spectrum ({})'.format(label, mother.name))
bx.set_ylabel('Period (years)')
#
Yticks = 2 ** numpy.arange(numpy.ceil(numpy.log2(period.min())),
numpy.ceil(numpy.log2(period.max())))
bx.set_yticks(numpy.log2(Yticks))
bx.set_yticklabels(Yticks)
# Third sub-plot, the global wavelet and Fourier power spectra and theoretical
# noise spectra. Note that period scale is logarithmic.
cx = pyplot.axes([0.77, 0.37, 0.2, 0.28], sharey=bx)
cx.plot(glbl_signif, numpy.log2(period), 'k--')
cx.plot(var * fft_theor, numpy.log2(period), '--', color='#cccccc')
cx.plot(var * fft_power, numpy.log2(1./fftfreqs), '-', color='#cccccc',
linewidth=1.)
cx.plot(var * glbl_power, numpy.log2(period), 'k-', linewidth=1.5)
cx.set_title('c) Global Wavelet Spectrum')
cx.set_xlabel(r'Power [({})^2]'.format(units))
cx.set_xlim([0, glbl_power.max() + var])
cx.set_ylim(numpy.log2([period.min(), period.max()]))
cx.set_yticks(numpy.log2(Yticks))
cx.set_yticklabels(Yticks)
pyplot.setp(cx.get_yticklabels(), visible=False)
# Fourth sub-plot, the scale averaged wavelet spectrum.
dx = pyplot.axes([0.1, 0.07, 0.65, 0.2], sharex=ax)
dx.axhline(scale_avg_signif, color='k', linestyle='--', linewidth=1.)
dx.plot(t, scale_avg, 'k-', linewidth=1.5)
dx.set_title('d) {}--{} year scale-averaged power'.format(2, 8))
dx.set_xlabel('Time (year)')
dx.set_ylabel(r'Average variance [{}]'.format(units))
ax.set_xlim([t.min(), t.max()])
pyplot.show()
得到如下结果:
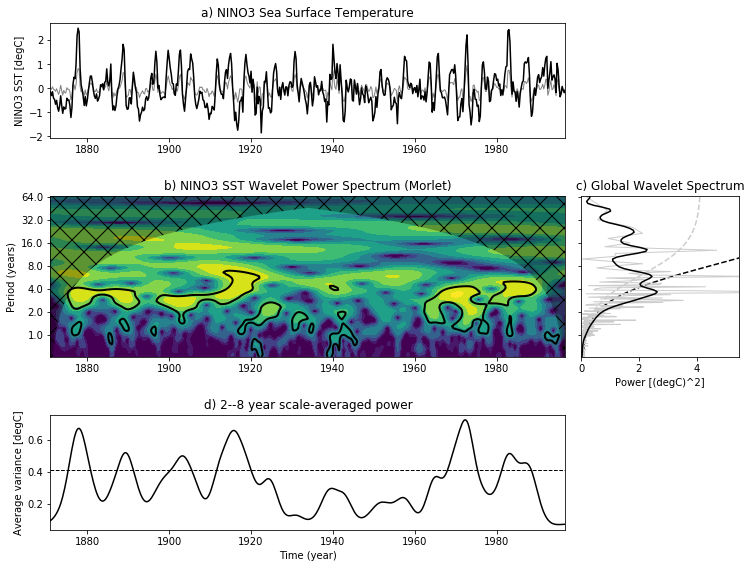
NINO3海表温度记录的小波分析:(a)时间序列(黑色实线)和小波逆变换(灰色实线),(b) Morlet小波(ω0=6)作为时间和傅里叶等效波周期(年)函数的归一化小波功率谱。黑色实线包围了相对于红噪声随机过程(α=0.77)置信度超过95%的区域。交叉孵化和阴影区域表示在母小波的影响锥的影响。(iii)全局小波功率谱(黑色实线)和傅立叶功率谱(灰色实线)。虚线表示95%置信水平。(iv) 28年波段尺度平均小波功率(黑色实线)、功率趋势(灰色实线)和95%置信水平(黑色虚线)。