21、乘积最大子数组

(1) 题目解析

一个正数，需要和正数相乘才能得到一个大的乘积，反之一个负数，需要和一个负数做乘积，才能得到一个大的乘积。

解决子数组问题，首先需要分 " 按长度 "进行分类。

(2) 算法原理

法子一:

可以看出，如果我们只是单独定义一个状态表达式，是不足以解决多种情况的。

法子二:

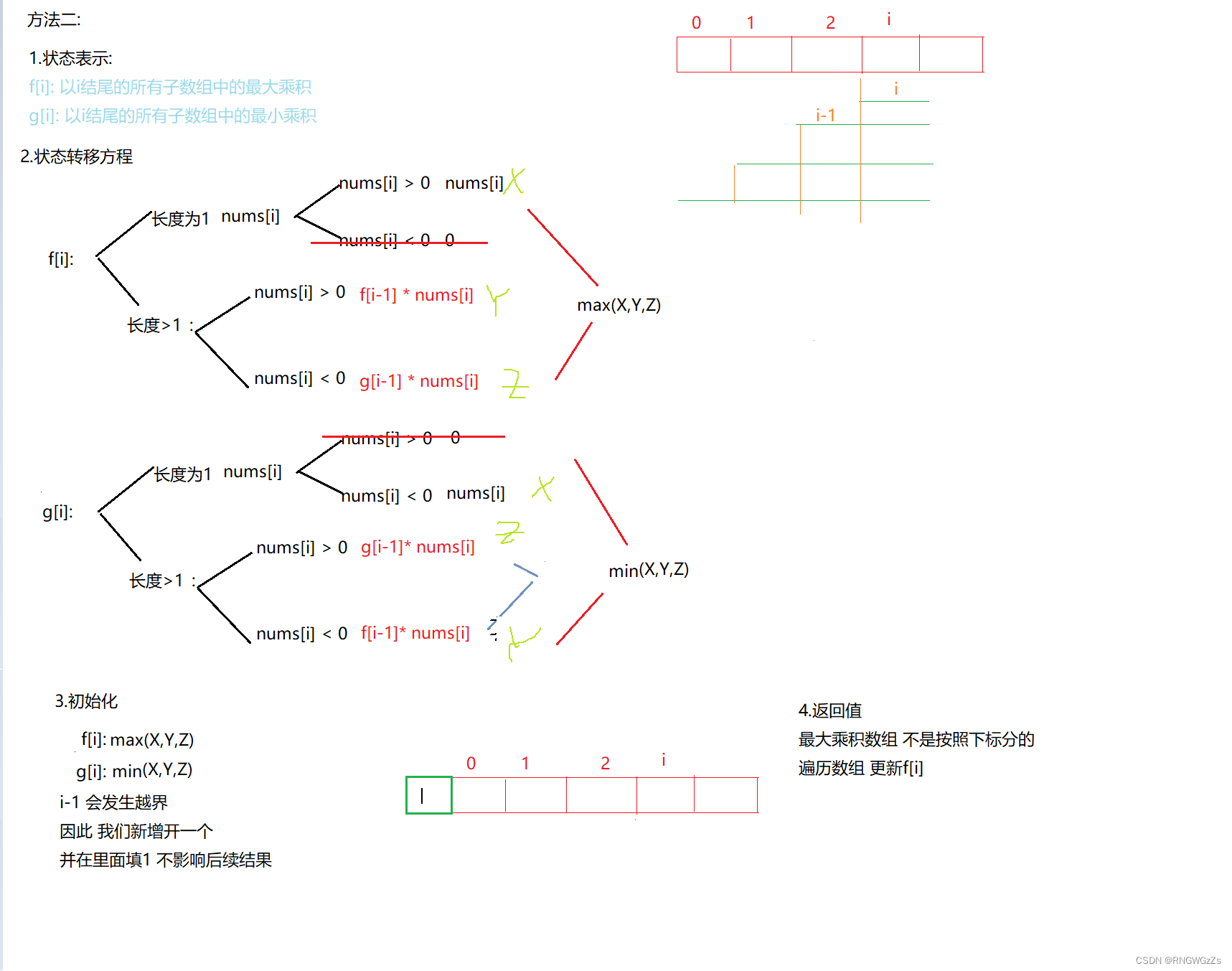
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();

        vector<int> f(n+1);
        auto g = f;
        f[0] = g[0] = 1;
        int ret = INT_MIN;
        for(int i=1; i<=n; ++i){    
            int x = nums[i-1],y=f[i-1]*nums[i-1],z=g[i-1]*nums[i-1];
            f[i] = max(x,max(y,z));
            g[i] = min(x,min(y,z));
            ret = max(ret,f[i]);
        }
        return ret;
    }
};

22、乘积为为正数的最长子数组长度

(1) 题目解析

这道题和上面的求乘积最大的子数组和有异曲同工之处，不过在这里是求的 "长度",而非乘积和。

(2) 算法原理

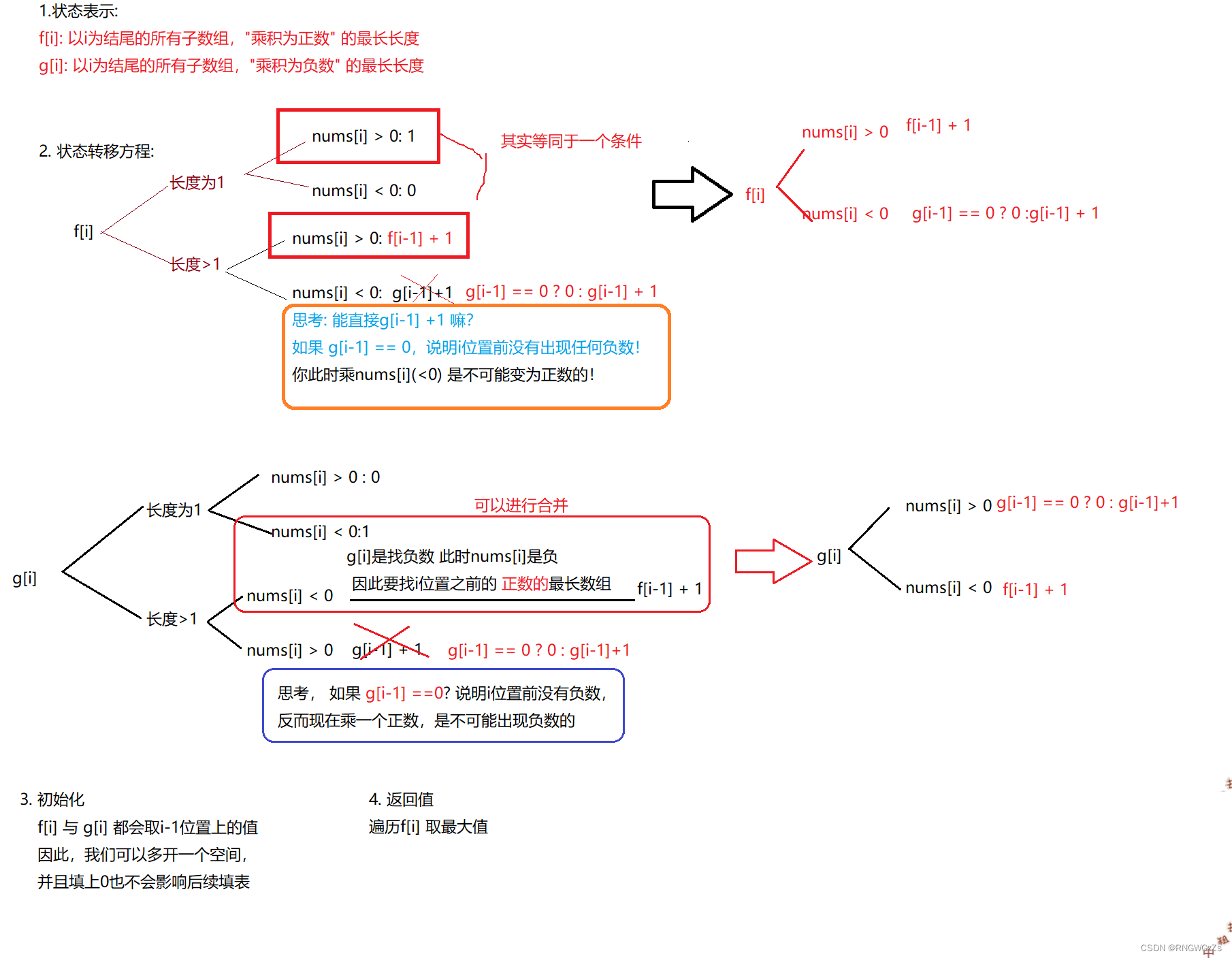
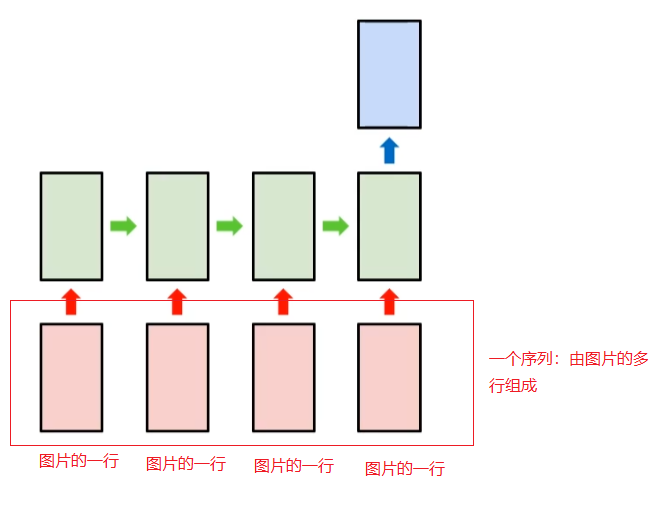
尤其注意nums[i]的几种状态，以及dp表达式表示的状态信息，根据这些信息进行分析画图。

class Solution {
public:
    int getMaxLen(vector<int>& nums) {
        int n = nums.size();

        vector<int> f(n+1);
        auto g = f;

        int ret = INT_MIN;
        for(int i=1; i<=n; ++i){
            if(nums[i-1] > 0)
            {
                 f[i] = f[i-1] + 1;
                 g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
            }
            else if(nums[i-1] < 0)
            {
                f[i] = g[i-1] ==0 ? 0 : g[i-1] + 1;
                g[i] = f[i-1] + 1;
            }
            ret = max(ret,f[i]);
        }
        return ret;
    }
};

23、等差数列划分

(1) 题目解析

(2) 算法原理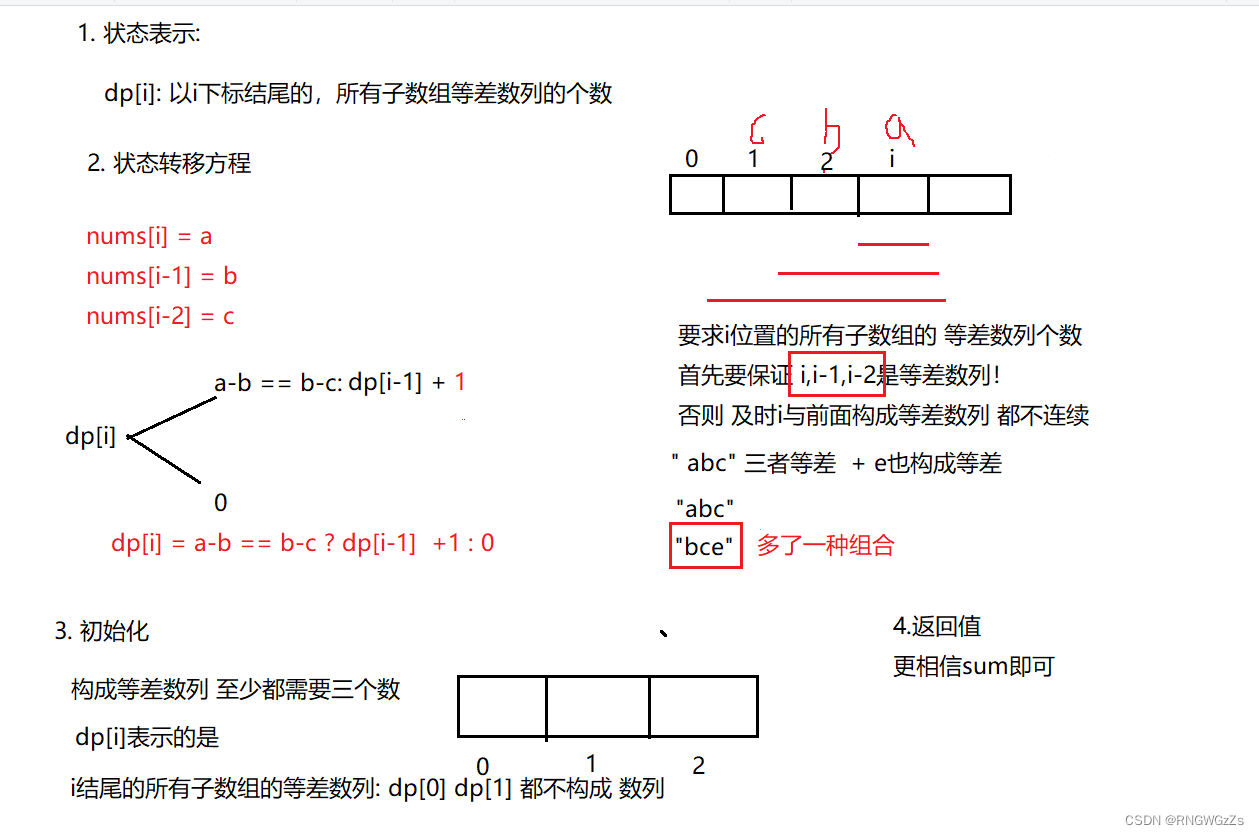

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n);
        int sum = 0;
        for(int i=2; i<n; ++i){
            if(nums[i] - nums[i-1] == nums[i-1]-nums[i-2]){
                dp[i] = dp[i-1] + 1;
            }
            else{
                dp[i] = 0;
            }
            sum += dp[i];
        }
        return sum;
    }
};

24、最长湍流子数组

(1) 题目解析

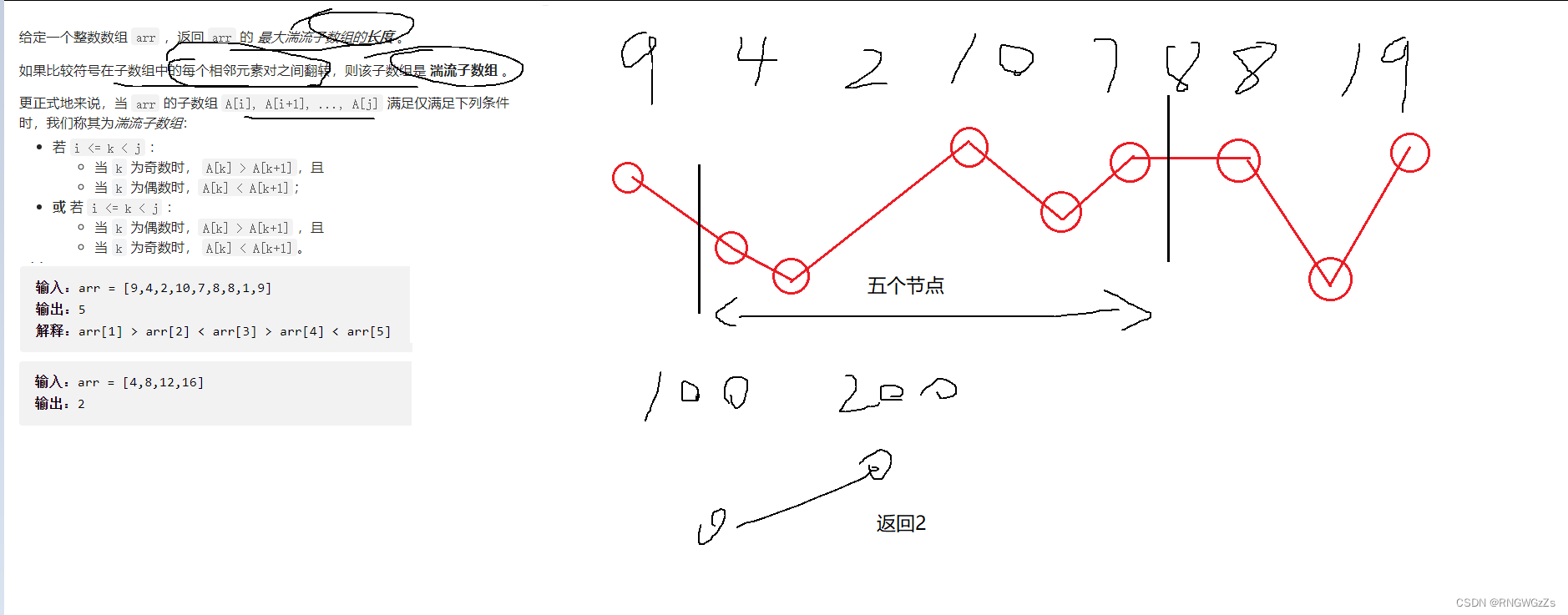
(2) 算法原理

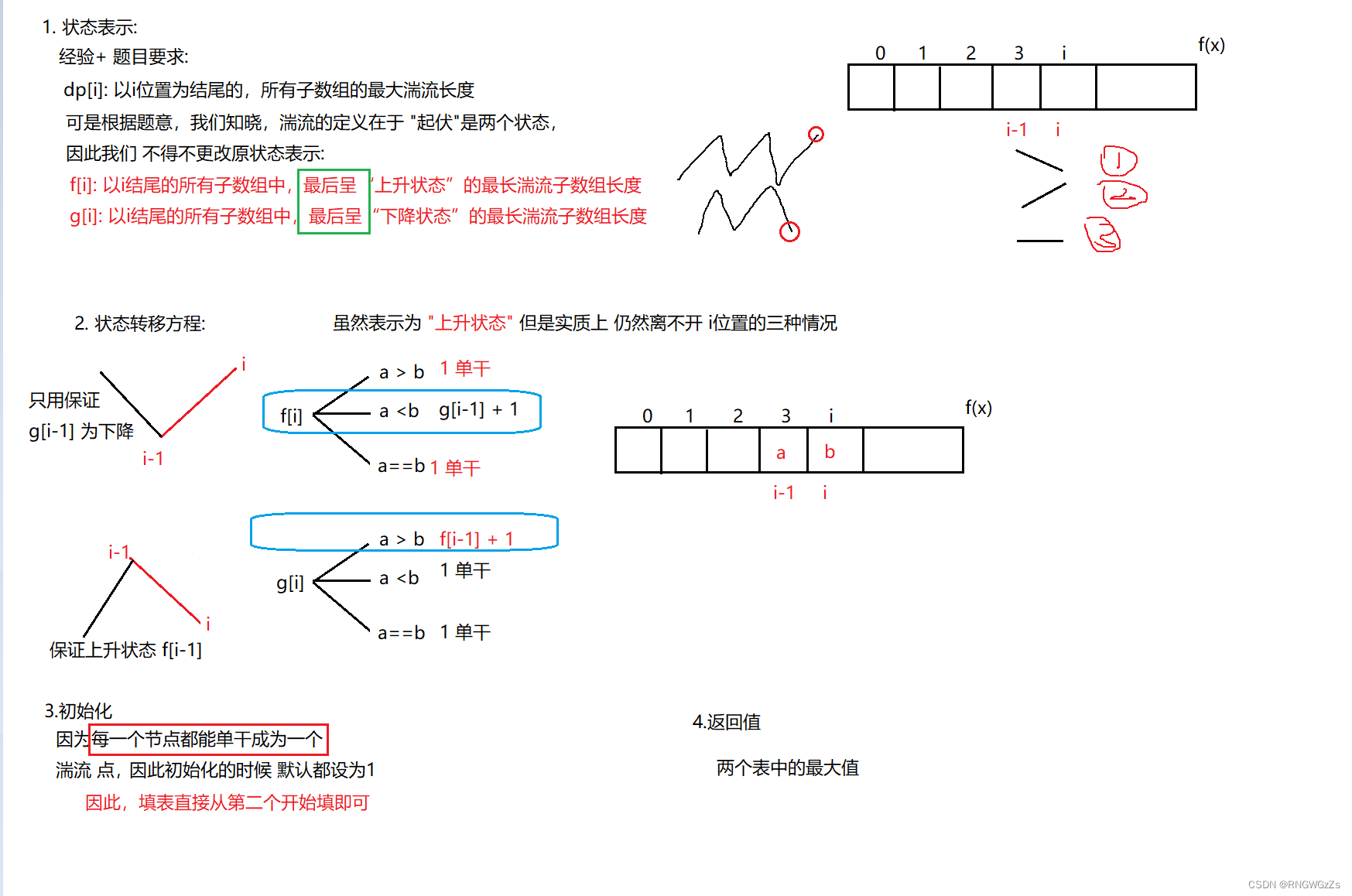
class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        int n = arr.size();
        vector<int> f(n,1);
        auto g = f;

        int ret = 1;
        for(int i=1; i<n; ++i){
            if(arr[i-1] < arr[i]) f[i] = g[i-1] + 1;
            else if(arr[i-1] > arr[i]) g[i] =  f[i-1] + 1;
            ret = max(ret,max(f[i],g[i]));
        }
        return ret;
    }
};

25、单词拆分

(1) 题目解析

(2) 算法原理

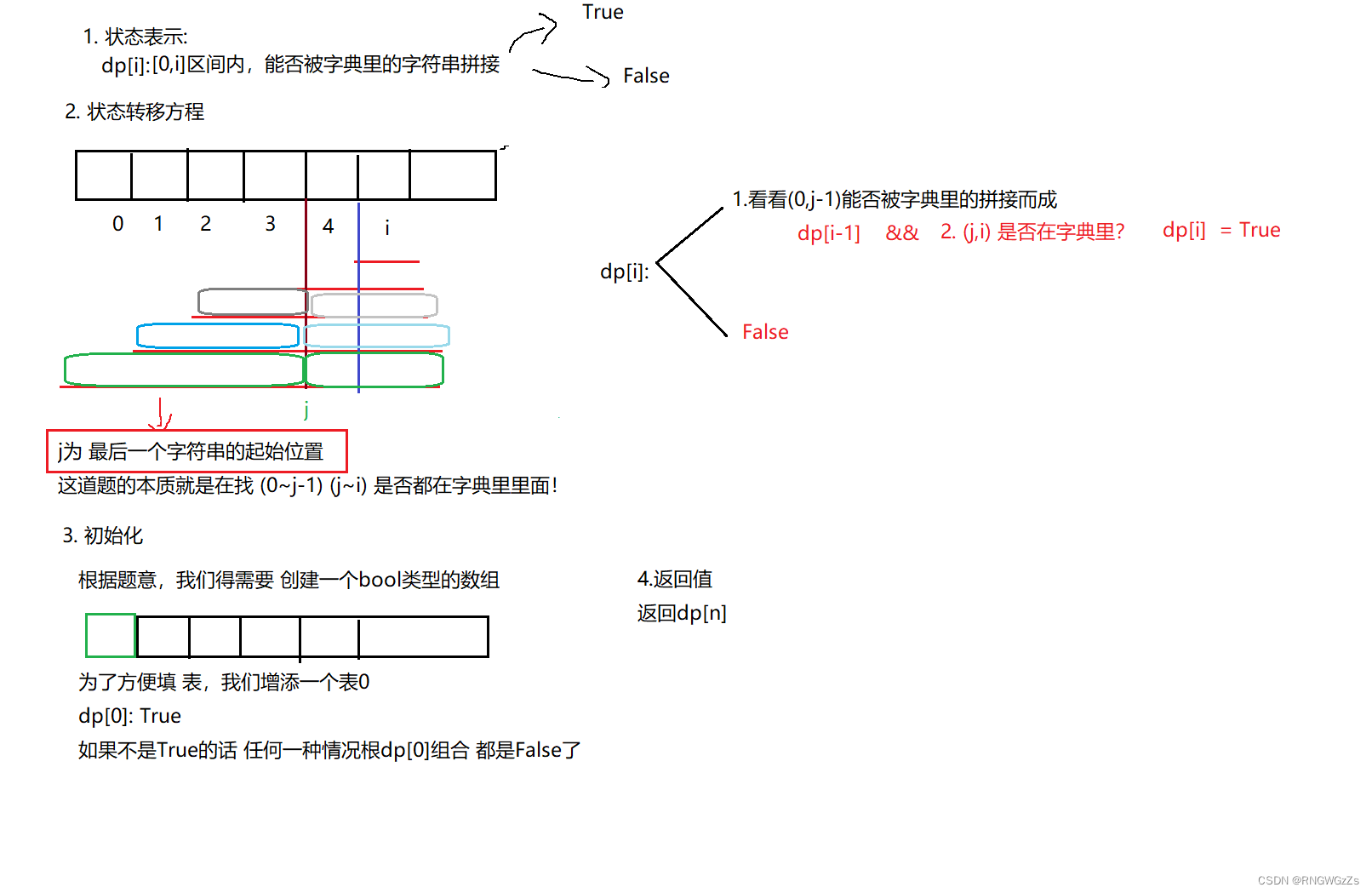对于这类隐藏的动规问题，理解题意尤为重要。如何将大问题，切分成子问题，那可得做大量练习，才能孰能生巧。

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> hash;
        for(auto& e:wordDict){
            hash.insert(e);
        }

        int n = s.size();
        vector<int> dp(n+1);
        dp[0] = true;
        s = ' ' + s;

        for(int i=1; i<=n; ++i){
            //(0,j-1) (j,i);
            for(int j=i; j>=1; --j){
                if(dp[j-1] && hash.count(s.substr(j,i - j + 1))){
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[n];
    }
};

本篇到此结束，感谢你的阅读

祝你好运，向阳而生~