分类目录:《自然语言处理从入门到应用》总目录
《自然语言处理从入门到应用——自然语言处理的语言模型(Language Model,LM)》中介绍了语言模型的基本概念,以及经典的基于离散符号表示的N元语言模型(N-gram Language Model)。从语言模型的角度来看,N元语言模型存在明显的缺点。首先,模型容易受到数据稀疏的影响,一般需要对模型进行平滑处理;其次,无法对长度超过N的上下文依赖关系进行建模。神经网络语言模型(Neural Network Language Model)在一定程度上克服了这些问题。一方面,通过引入词的分布式表示,也就是词向量,大大缓解了数据稀疏带来的影响;另一方面,利用更先进的神经网络模型结构(如循环神经网络、Transformer等),可以对长距离上下文依赖进行有效的建模。正因为这些优异的特性,加上语言模型任务本身无须人工标注数据的优势,神经网络语言模型几乎已经替代N元语言模型,成为现代自然语言处理中最重要的基础技术之一;同时,也是自然语言预训练技术的核心。本文将从最基本的前馈神经网络语言模型出发,介绍如何在大规模无标注文本数据上进行静态词向量的预训练;然后,介绍基于循环神经网络的语言模型,通过引入更丰富的长距离历史信息,进一步提升静态词向量的表示能力。
预训练任务
给定一段文本 w 1 w 2 ⋯ w n w_1w_2\cdots w_n w1w2⋯wn,语言模型的基本任务是根据历史上下文对下一时刻的词进行预测,也就是计算条件概率 P ( w t ∣ w 1 w 2 ⋯ w t − 1 ) P(w_t | w_1w_2\cdots w_{t-1}) P(wt∣w1w2⋯wt−1)。为了构建语言模型,可以将其转化为以词表为类别标签集合的分类问题,其输入为历史词序列 w 1 w 2 ⋯ w t − 1 w_1w_2\cdots w_{t-1} w1w2⋯wt−1(也记作 w 1 : t − 1 w_{1:t -1} w1:t−1),输出为目标词 w t w_t wt。然后就可以从无标注的文本语料中构建训练数据集,并通过优化该数据集上的分类损失(如交叉熵损失或负对数似然损失)对模型进行训练。由于监督信号来自数据自身,因此这种学习方式也被称为自监督学习(Self-supervised Learning)。
在讨论模型的具体实现方式之前,首先面临的一个问题是:如何处理动态长度的历史词序列(模型输入)?一个直观的想法是使用词袋表示,但是这种表示方式忽略了词的顺序信息,语义表达能力非常有限。下文将介绍前馈神经网络语言模型(Feed-forward Neural Network Language Model)以及循环神经网络语言模型(Recurrent Neural Network Language Model,RNNLM),分别从数据和模型的角度解决这一问题。
前馈神经网络语言模型
前馈神经网络语言模型利用了传统N元语言模型中的马尔可夫假设(Markov Assumption)——对下一个词的预测只与历史中最近的
n
−
1
n−1
n−1个词相关。从形式上看:
P
(
w
t
∣
w
1
:
t
−
1
)
=
P
(
w
t
∣
w
t
−
n
+
1
:
t
−
1
)
P(w_t | w_{1:t-1}) = P(w_t | w_{t-n+1:t-1})
P(wt∣w1:t−1)=P(wt∣wt−n+1:t−1)
因此,模型的输入变成了长度为
n
−
1
n−1
n−1的定长词序列
w
t
−
n
+
1
:
t
−
1
w_{t−n+1:t−1}
wt−n+1:t−1,模型的任务也转化为对条件概率
P
(
w
t
∣
w
t
−
n
+
1
:
t
−
1
)
P(w_t | w_{t-n+1:t-1})
P(wt∣wt−n+1:t−1) 进行估计。前馈神经网络由输入层、词向量层、隐藏层和输出层构成。在前馈神经网络语言模型中,词向量层首先对输入层长为
n
−
1
n−1
n−1的历史词序列
w
t
−
n
+
1
:
t
−
1
w_{t-n+1:t-1}
wt−n+1:t−1进行编码,将每个词表示为一个低维的实数向量,即词向量;然后,隐藏层对词向量层进行线性变换,并使用激活函数实现非线性映射;最后,输出层通过线性变换将隐藏层向量映射至词表空间,再通过Softmax函数得到在词表上的归一化的概率分布,如下图所示:
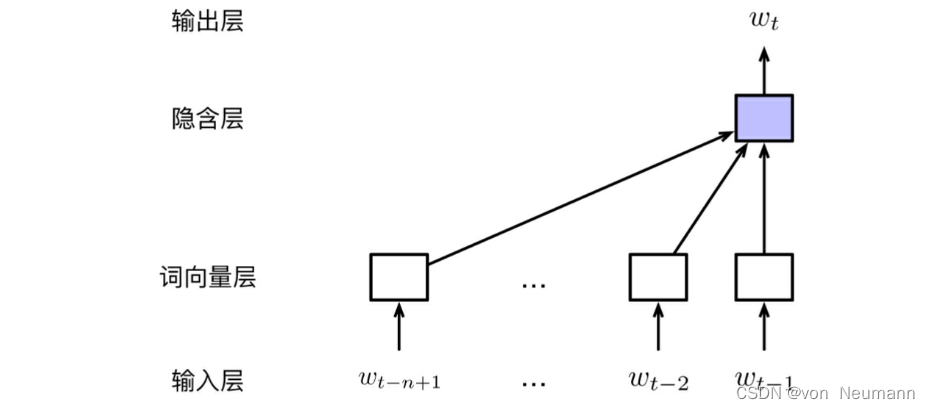
上图的模型包含如下几个部分:
- 输入层:模型的输入层由当前时刻 t t t的历史词序列 w t − n + 1 : t − 1 w_{t-n+1:t-1} wt−n+1:t−1构成,主要为离散的符号表示。在具体实现中,既可以使用每个词的独热编码(One-Hot Encoding),也可以直接使用每个词在词表中的位置下标。
- 词向量层:词向量层将输入层中的每个词分别映射至一个低维、稠密的实值特征向量。词向量层也可以理解为一个查找表(Look-up Table),获取词向量的过程,也就是根据词的索引从查找表中找出对应位置的向量的过程: x = [ v w t − n + 1 ; v w t − n + 2 ; ⋯ ; v w t − 1 ; ] x=[v_{w_{t-n+1}}; v_{w_{t-n+2}}; \cdots;v_{w_{t-1}};] x=[vwt−n+1;vwt−n+2;⋯;vwt−1;]式中, v w ∈ R d v_w\in R^d vw∈Rd表示词 w w w的 d d d维词向量( d ≪ ∣ V ∣ d\ll|V| d≪∣V∣, ∣ V ∣ |V| ∣V∣为词表大小); x ∈ R ( n − 1 ) d x\in R^{(n-1)d} x∈R(n−1)d表示历史序列中所有词向量拼接之后的结果。若定义词向量矩阵为 E ∈ R d × ∣ V ∣ E\in R^{d\times|V|} E∈Rd×∣V∣,那么 v w v_w vw即为 E E E中与 w w w对应的列向量,也可以表示为 E E E与 w w w的独热编码 e w e_w ew之间的点积。
- 隐藏层:模型的隐藏层对词向量层 x x x进行线性变换与激活。令 W hid ∈ R m × ( n − 1 ) d W^\text{hid}\in R^{m\times(n-1)d} Whid∈Rm×(n−1)d为输入层到隐藏层之间的线性变换矩阵, b hid ∈ R m b^\text{hid}\in R^m bhid∈Rm为偏置项, m m m为隐藏层维度。隐藏层可以表示为: h = f ( W hid x + b hid ) h=f(W^\text{hid}x+b^\text{hid}) h=f(Whidx+bhid)式中, f f f是激活函数。常用的激活函数有Sigmoid、tanh和ReLU等。
- 输出层:模型的输出层对 h h h做线性变换,并利用Softmax函数进行归一化,从而获得词表 V V V空间内的概率分布。令 W out W^{\text{out}} Wout为隐藏层到输出层之间的线性变换矩阵,相应的偏置项为 b out b^{\text{out}} bout。输出层可由下式计算: y = Softmax ( W out x + b out ) y=\text{Softmax}(W^{\text{out}}x+b^{\text{out}}) y=Softmax(Woutx+bout)
综上所述,前馈神经网络语言模型的自由参数包含词向量矩阵
E
E
E,词向量层与隐藏层之间的权值矩阵
W
hid
W^\text{hid}
Whid及偏置项
b
hid
b^\text{hid}
bhid,隐藏层与输出层之间的权值矩阵
W
out
W^{\text{out}}
Wout与偏置项
b
out
b^{\text{out}}
bout,可以记为:
θ
=
{
E
,
W
hid
,
b
hid
,
W
out
,
b
out
}
\theta=\{E, W^\text{hid}, b^\text{hid}, W^{\text{out}}, b^{\text{out}}\}
θ={E,Whid,bhid,Wout,bout}
参数数量为 ∣ V ∣ × d + m × ( n − 1 ) d + m + ∣ V ∣ × m + ∣ V ∣ |V|\times d+m\times(n-1)d+m+|V|\times m+|V| ∣V∣×d+m×(n−1)d+m+∣V∣×m+∣V∣,即 ( 1 + m + d ) ∣ V ∣ + ( 1 + ( n − 1 ) d ) m (1+m+d)|V|+(1+(n-1)d)m (1+m+d)∣V∣+(1+(n−1)d)m。由于 m m m和 d d d是常数,所以,模型的自由参数数量随词表大小呈线性增长,且 n n n的增大并不会显著增加参数的数量。另外,词向量维度 d d d、隐藏层维度 m m m和输入序列长度 n − 1 n−1 n−1等超参数的调优需要在开发集上进行。模型训练完成后,矩阵 E E E则为预训练得到的静态词向量。
循环神经网络语言模型
在前馈神经网络语言模型中,对下一个词的预测需要回看多长的历史是由超参数
n
n
n决定的。但是,不同的句子对历史长度
n
n
n的期望往往是变化的。例如,对于句子“他 喜欢 吃 苹果”,根据“吃”容易推测出,下画线处的词有很大概率是一种食物。因此,只需要考虑较短的历史就足够了。而对于结构较为复杂的句子,如“他 感冒 了,于是 下班 之后 去 了 医院”,则需要看到较长的历史“感冒”才能合理地预测出目标词“医院”。循环神经网络语言模型正是为了处理这种不定长依赖而设计的一种语言模型。循环神经网络是用来处理序列数据的一种神经网络,而自然语言正好满足这种序列结构性质。循环神经网络语言模型中的每一时刻都维护一个隐含状态,该状态蕴含了当前词的所有历史信息,且与当前词一起被作为下一时刻的输入。这个随时刻变化而不断更新的隐含状态也被称作记忆(Memory)。下图展示了循环神经网络语言模型的基本结构:
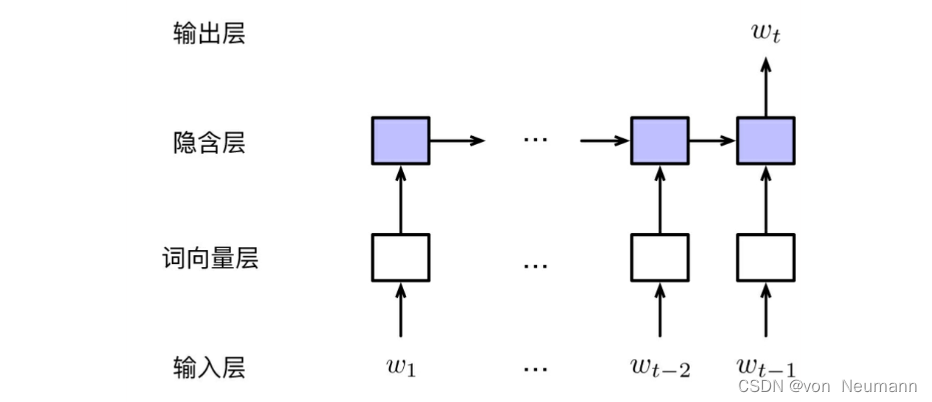
上图的模型包含如下几个部分:
- 输入层:与前馈神经网络语言模型不同,由于模型不再受限于历史上下文的长度,所以此时输入层可由完整的历史词序列构成,即 w 1 : t − 1 w_{1:t−1} w1:t−1。
- 词向量层:与前馈神经网络语言模型类似,输入的词序列首先由词向量层映射至相应的词向量表示。那么,在
t
t
t时刻的输入将由其前一个词
w
t
−
1
w_{t−1}
wt−1的词向量以及
t
−
1
t−1
t−1时刻的隐含状态
h
t
−
1
h_{t−1}
ht−1组成。令
w
0
w_0
w0为句子起始标记(如:
<bos>), h 0 h_0 h0为初始隐含层向量(可使用0向量),则t时刻的输入可以表示为: x t = [ v w t − 1 ; h t − 1 ] x_t=[v_{w_{t-1}}; h_{t-1}] xt=[vwt−1;ht−1] - 隐含层:隐含层的计算与前馈神经网络语言模型类似,由线性变换与激活函数构成。 h t = tanh ( W hid x t + b hid ) h_t=\text{tanh}(W^{\text{hid}}x_t+b^{\text{hid}}) ht=tanh(Whidxt+bhid)式中 W hid ∈ R m × ( d + m ) W^{\text{hid}}\in R^{m\times(d+m)} Whid∈Rm×(d+m), b hid ∈ R m b^{\text{hid}}\in R^m bhid∈Rm。 W hid W^{\text{hid}} Whid实际上由两部分构成,即 W hid = [ U ; V ] W^{\text{hid}}=[U; V] Whid=[U;V]且 U ∈ R m × d U\in R^{m\times d} U∈Rm×d、 V ∈ R m × m V\in R^{m\times m} V∈Rm×m分别是 v w t − 1 v_{w_{t-1}} vwt−1、 h t − 1 h_{t−1} ht−1与隐含层之间的权值矩阵。为了体现循环神经网络的递归特性,在书写时常常将两者区分开: h t = tanh ( U v w t − 1 + V h t − 1 + b hid ) h_t=\text{tanh}(Uv_{w_{t-1}}+Vh_{t-1}+b^{\text{hid}}) ht=tanh(Uvwt−1+Vht−1+bhid)
- 输出层:最后,在输出层计算t时刻词表上的概率分布: y = Softmax ( W out x + b out ) y=\text{Softmax}(W^{\text{out}}x+b^{\text{out}}) y=Softmax(Woutx+bout)式中, W out ∈ R ∣ V ∣ × m W^{\text{out}}\in R^{|V|\times m} Wout∈R∣V∣×m。
以上只是循环神经网络最基本的形式,当序列较长时,训练阶段会存在梯度弥散(Vanishing gradient)或者梯度爆炸(Exploding gradient)的风险(可以参看文章《机器学习中的数学——深度学习优化的挑战:梯度消失和梯度爆炸》)。为了应对这一问题,以前的做法是在梯度反向传播的过程中按长度进行截断(Truncated Back-propagation Through Time),从而使得模型能够得到有效的训练,但是与此同时,也减弱了模型对于长距离依赖的建模能力。这种做法一直持续到2015年左右,之后被含有门控机制的循环神经网络,如长短时记忆网络(LSTM)代替。
参考文献:
[1] 车万翔, 崔一鸣, 郭江. 自然语言处理:基于预训练模型的方法[M]. 电子工业出版社, 2021.
[2] 邵浩, 刘一烽. 预训练语言模型[M]. 电子工业出版社, 2021.
[3] 何晗. 自然语言处理入门[M]. 人民邮电出版社, 2019
[4] Sudharsan Ravichandiran. BERT基础教程:Transformer大模型实战[M]. 人民邮电出版社, 2023
[5] 吴茂贵, 王红星. 深入浅出Embedding:原理解析与应用实战[M]. 机械工业出版社, 2021.