---

---

笔记_2

图像尺寸变换

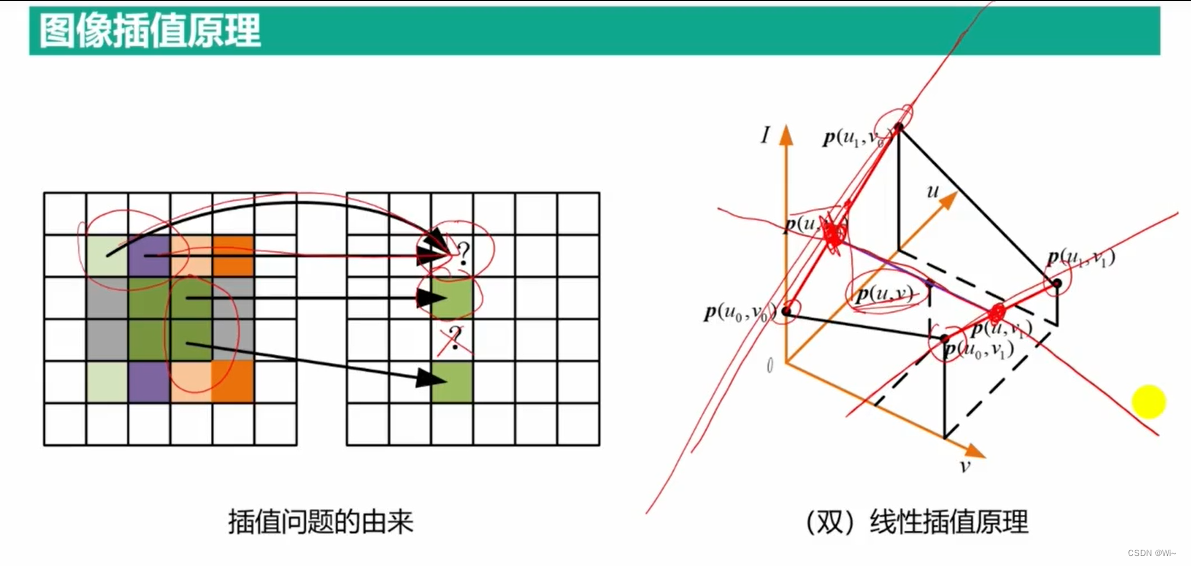
最邻近法
选择临近的像素。简单，效果较差

线性插值法
选择临近两个像素，建立一次函数，进行投影，得到的数据

双线性插值法
选择临近的四个像素，四个像素两两建立一次函数，再把像素投影到建立好的一次函数上再次建立一次函数得到数据。
应用图像的拉伸变换、旋转、仿射变换、透视变换等涉及到对图像像素位置改变的情况。

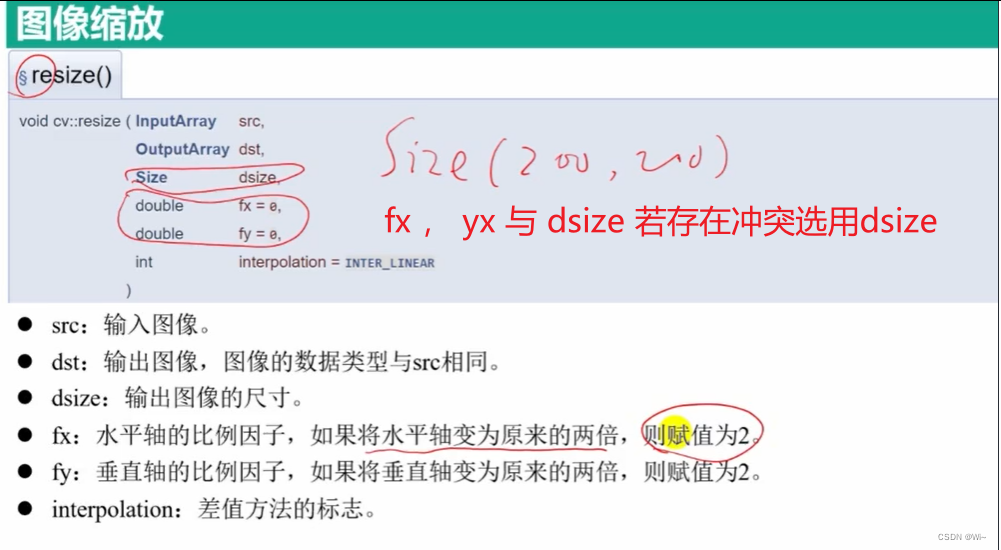
resize 图像缩放 （重置图像大小)

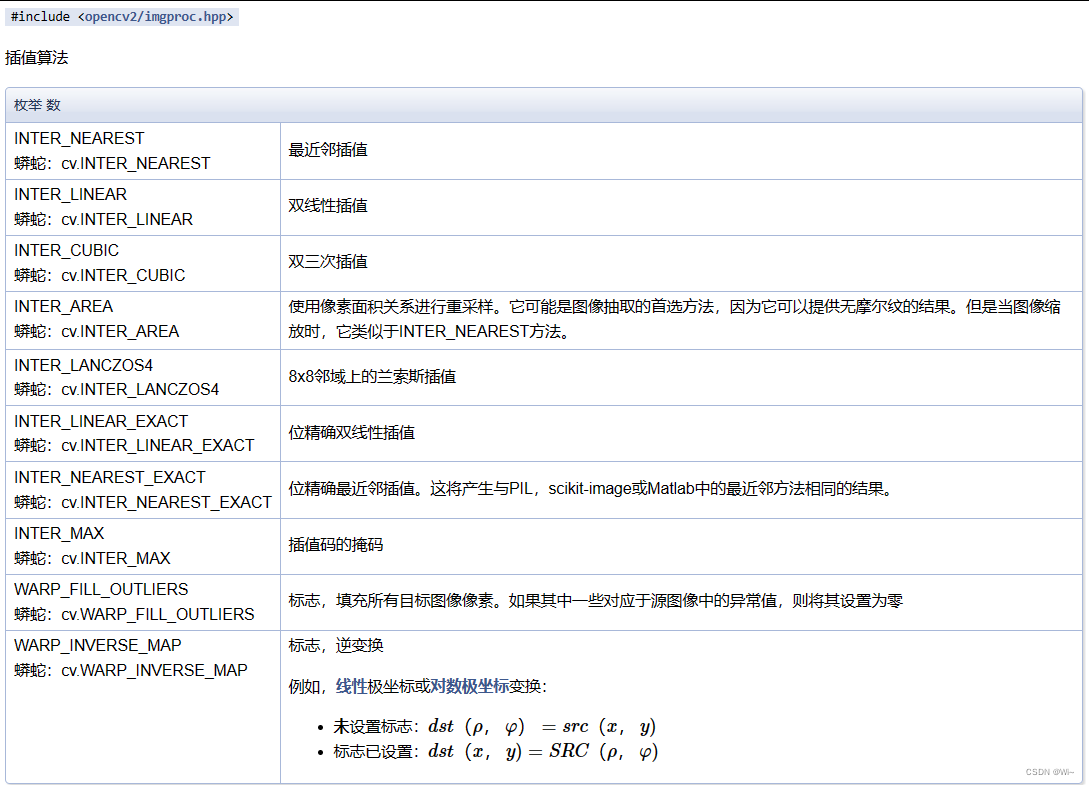
interpolation标志

flip 图像翻转

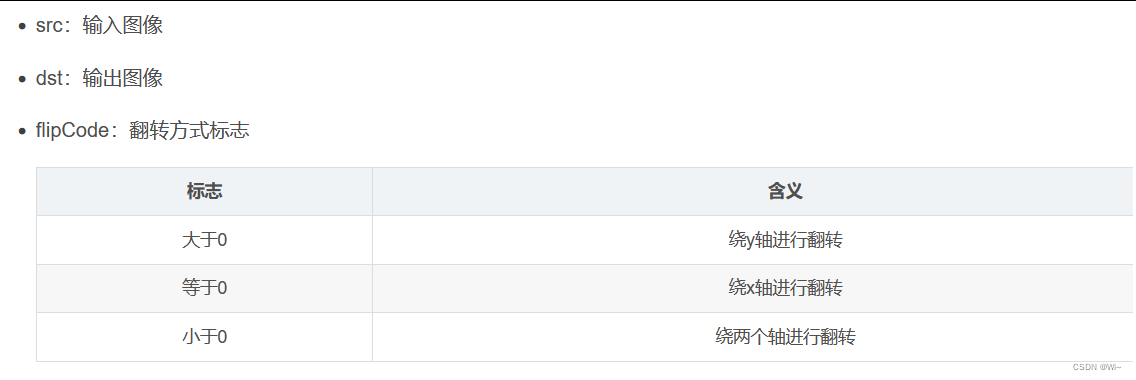
hconcat 横向连接

vconcat 纵向连接

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
			return -1;
	}
	
	//imwrite("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lenaleftTop.jpg", leftTop);
	//imwrite("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lenarightTop.jpg", rightTop);
	//imwrite("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lenaleftDown.jpg", leftDown);
	//imwrite("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lenarightDown.jpg", rightDown);
	Mat gray;
	cvtColor(img, gray, COLOR_BGR2GRAY);
	Mat smallImg, bigImg0, bigImg1, bigImg2;
	//先将图像缩小
	resize(gray, smallImg, Size(50, 50), 0, 0, INTER_AREA);
	//最近邻插值
	resize(smallImg, bigImg0, Size(100, 100), 0, 0, INTER_NEAREST);
	//双线性插值
	resize(smallImg, bigImg1, Size(100, 100), 0, 0, INTER_LINEAR);
	//双三次插值
	resize(smallImg, bigImg2, Size(100, 100), 0, 0, INTER_CUBIC);



	//翻转图像
	Mat img_x, img_y, img_xy;
	//等于0，沿x轴翻转
	flip(gray, img_x, 0);
	//大于0，沿y轴翻转
	flip(gray, img_x, 1);
	//小于0，沿xy轴翻转（原点翻转）
	flip(gray, img_x, -1);

	
	//平均分割图像四个部分
	//Range(*,*) 按照矩阵中的元素抠图

	Mat leftTop = Mat(img, Range(0, img.rows / 2), Range(0, img.cols / 2));
	Mat rightTop = Mat(img, Range(0, img.rows / 2), Range(img.cols / 2, img.cols));
	Mat leftDown = Mat(img, Range(img.rows / 2, img.rows), Range(0, img.cols / 2));
	Mat rightDown = Mat(img, Range(img.rows / 2, img.rows), Range(img.cols / 2, img.cols));


	//图像拼接
	Mat img0, img1, img_img;
	//图像横向连接，图像通道，高度y一致
	hconcat(leftTop, rightTop, img0);
	hconcat(leftDown, rightDown, img1);
	//图像纵向连接，图像通道，宽度x一致
	vconcat(img0, img1, img_img);

图像方式变换

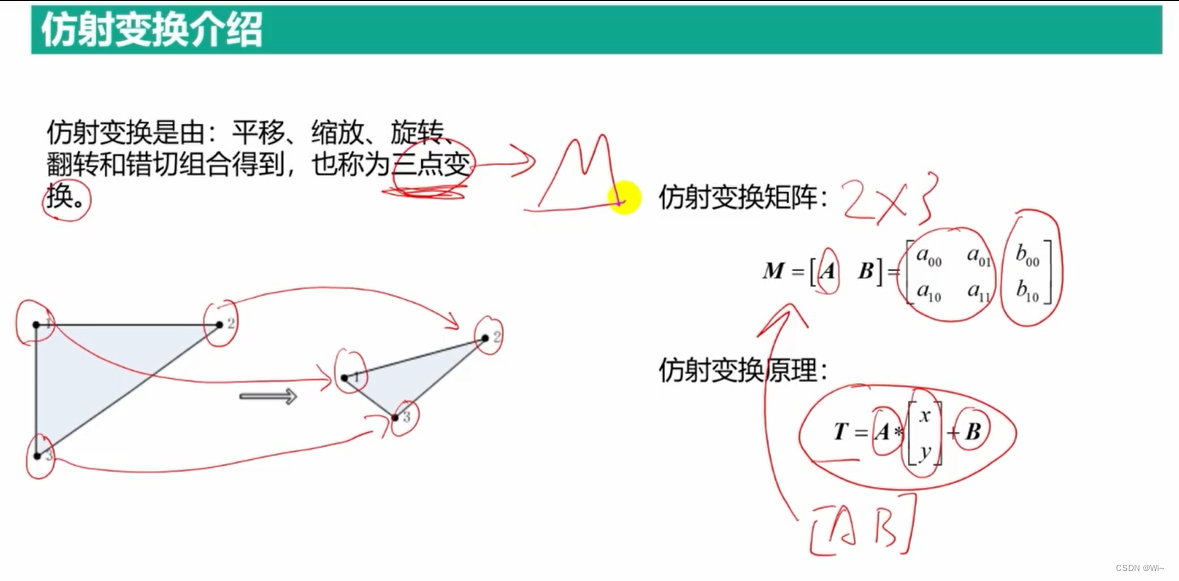
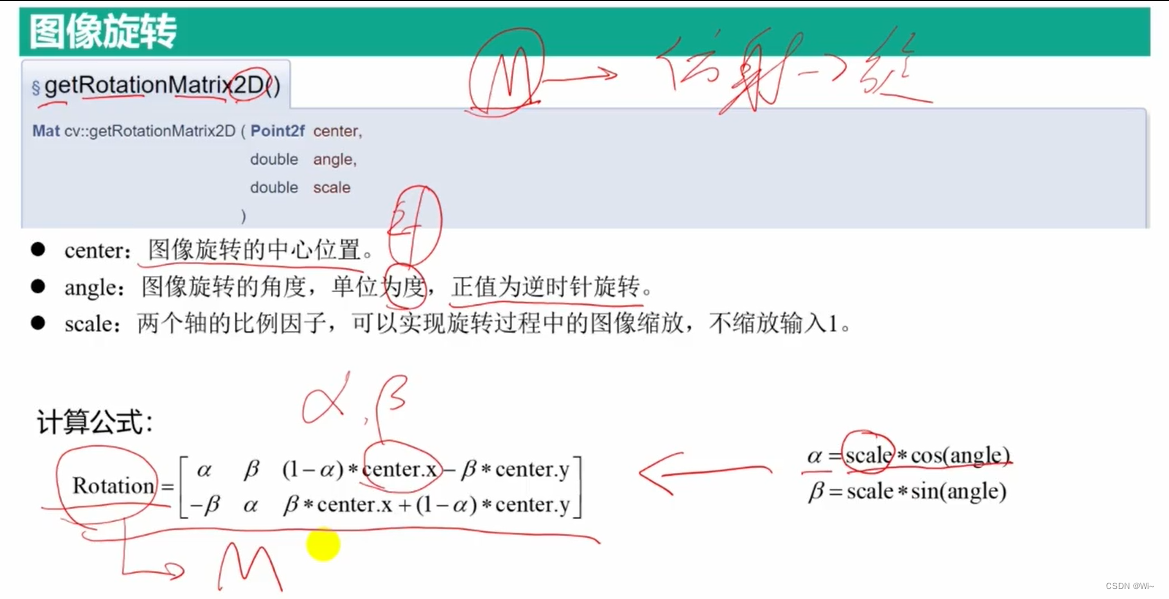
warpAffine 仿射变换函数：矩阵M（2*3）

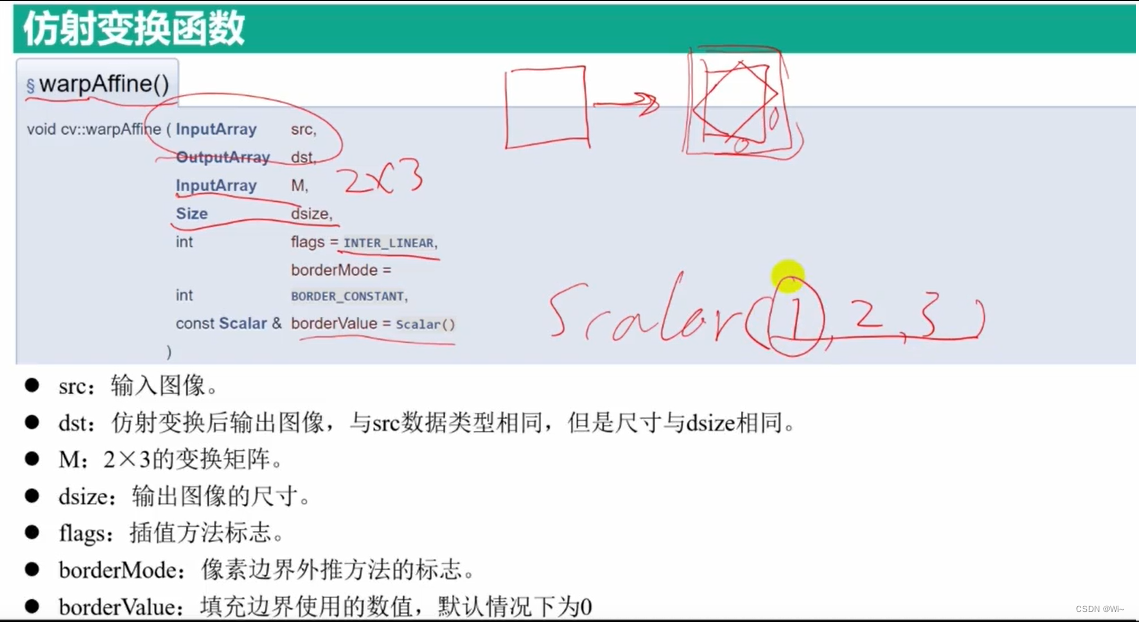
最常用的用特定值填充，BORDER_CONSTANT

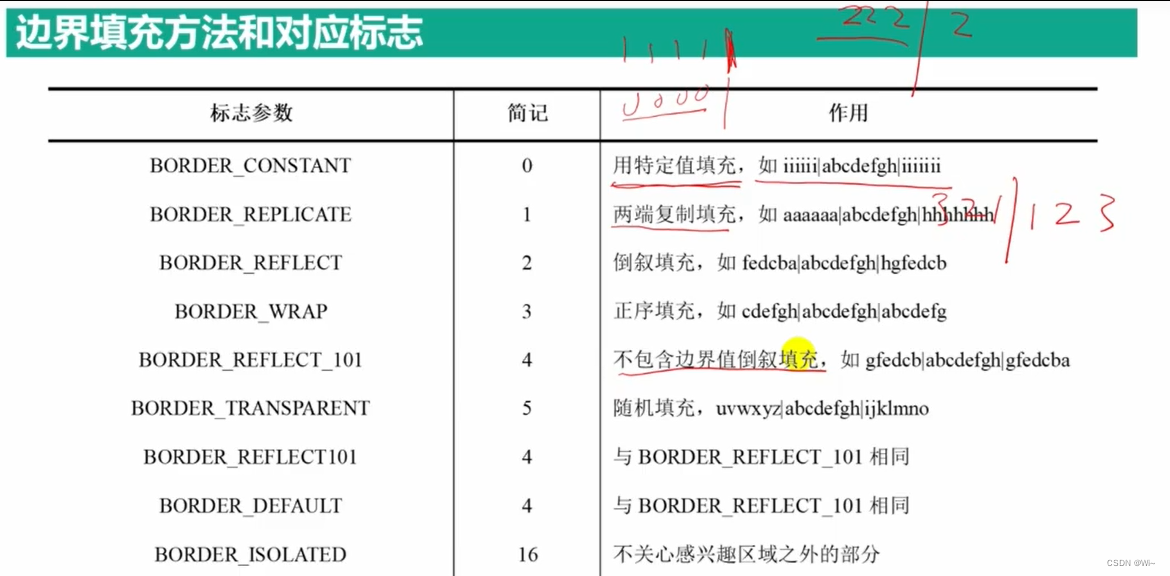
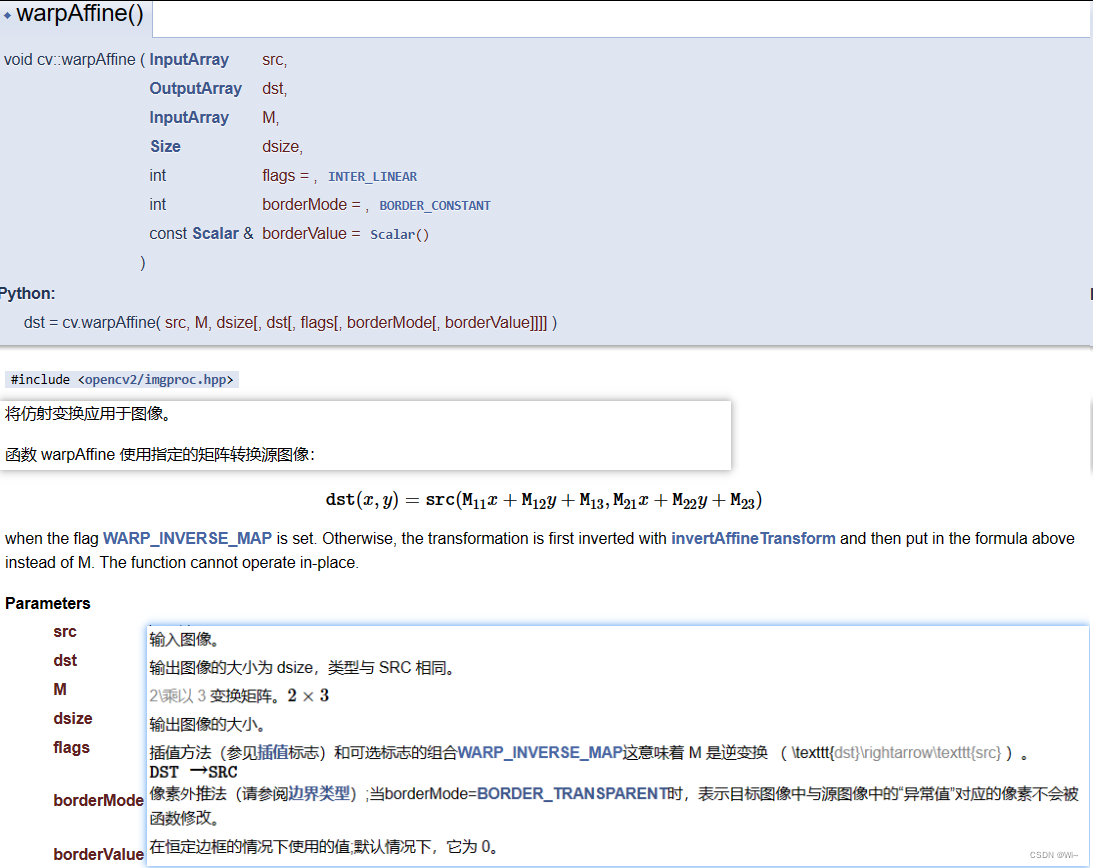
getRotationMatrix2D 获取图像旋转矩阵M：矩阵M（2*3）

getAffineTransform 获取仿射变换矩阵M：矩阵M（2*3）

代码演示

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
			return -1;
	}

	Mat rotation0, img_warp0;
	//设置图像旋转的角度
	double angle = 30;
	//Size(宽，高) 设置输出图像的尺寸
	Size dst_size(img.rows+100, img.cols+100);
	//设置图像的旋转中心
	Point2f center(img.rows / 2.0, img.cols / 2.0);
	//计算仿射变换矩阵(旋转矩阵)
	rotation0 = getRotationMatrix2D(center, angle, 1);
	//进行仿射变换
	warpAffine(img, img_warp0, rotation0, dst_size);




	//根据定义的三个点进行仿射变换
	Point2f src_points[3];
	Point2f dst_points[3];

	src_points[0] = Point2f(0, 0);
	src_points[1] = Point2f(5, 50);
	src_points[2] = Point2f(30, 90);

	dst_points[0] = Point2f(2, 5);
	dst_points[1] = Point2f(33, 55);
	dst_points[2] = Point2f(100, 150);


	Mat rotation1, img_warp1;
	//计算仿射变换矩阵
	rotation1 = getAffineTransform(src_points, dst_points);
	//进行仿射变换
	warpAffine(img, img_warp1, rotation1, dst_size);

图像透视变换

getPerspectiveTransform ：获取透视变换矩阵M（3*3）

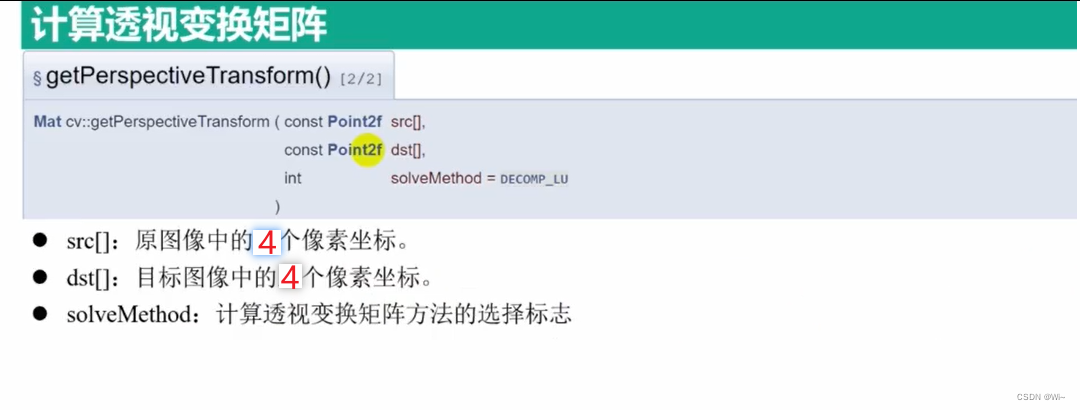
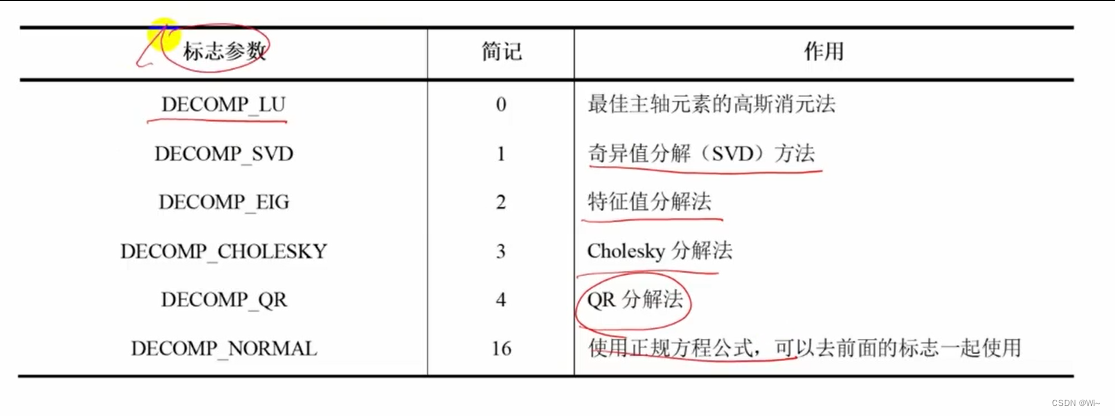
warpPerspective ：透视变换矩阵M（3*3）

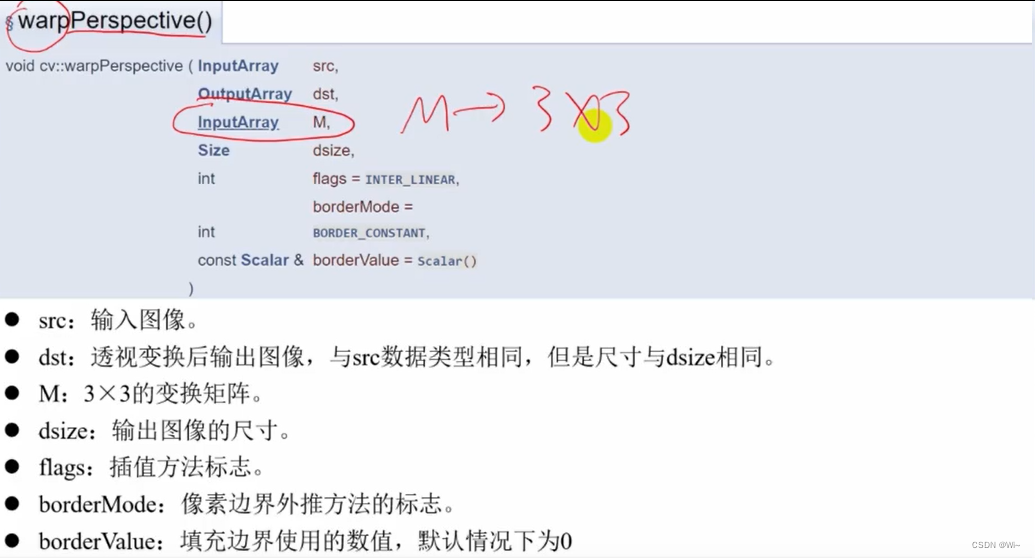
代码演示

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/modules/core/misc/objc/test/resources/chessboard.jpg");
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}
	Point2f src_points[4];
	Point2f dst_points[4];
	//获取原图像四个坐标
	src_points[0] = Point2f(224, 61);
	src_points[1] = Point2f(535, 46);
	src_points[2] = Point2f(231, 281);
	src_points[3] = Point2f(528, 302);

	//期望透视变换后四个坐标的位置
	dst_points[0] = Point2f(0, 0);
	dst_points[1] = Point2f(0, 500);
	dst_points[2] = Point2f(500, 0);
	dst_points[3] = Point2f(500, 500);

	Mat perspectiveMat, img_warp;
	//计算获取透视变换矩阵
	perspectiveMat = getPerspectiveTransform(src_points, dst_points);
	//进行透视变换
	warpPerspective(img, img_warp, perspectiveMat, Size(500,500));

图像中绘制基本图形

line 绘制直线

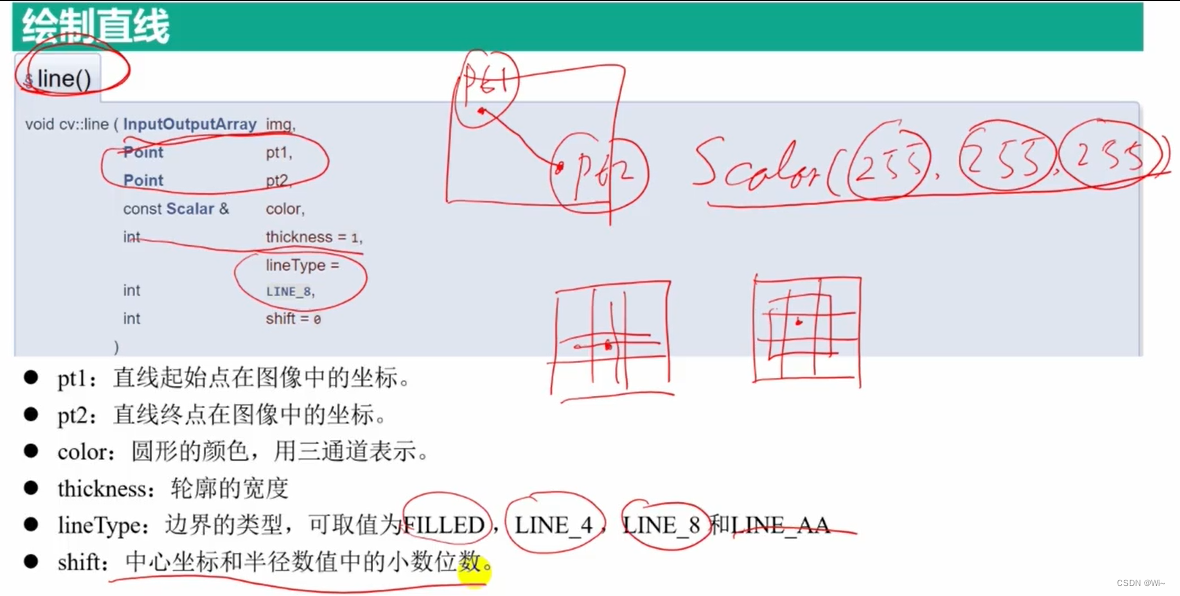
color：线条的颜色，可以是一个标量值，也可以是一个三元素元组，分别表示BGR三个通道的颜色值；
thickness：线条的粗细，默认为1；

lineType  怎么理解?
cv2.LINE_4：表示绘制4连接线，即线条的端点只与相邻的4个像素相连；
cv2.LINE_8：表示绘制8连接线，即线条的端点可以与相邻的8个像素相连；
cv2.LINE_AA：表示绘制抗锯齿线条。
其中，4连接线表示线条的端点只与相邻的4个像素相连，8连接线表示线条的端点可以与相邻的8个像素相连，
而抗锯齿线条则可以使线条的显示更加平滑。可以看出，不同类型的线条在显示效果和绘制速度上都有所不同。


shift参数理解?
shift参数用于指定坐标点小数部分的位数，通常情况下可以将它设置为0。
如果shift的值为0，则坐标点将被解释为整数坐标值。如果shift的值为1，则坐标点将被解释为包含一位小数的坐标值，以此类推。
在实际应用中，shift参数通常用于提高坐标精度。例如，在一些需要精细控制图像变换的场景中，
可以将shift设置为较大的值，使得坐标点的小数部分可以更精细地表示。
但是需要注意的是，如果shift的值过大，可能会导致计算量增大，从而影响程序的执行效率。通常情况下，可以根据实际需求选择适当的shift值。

arrowedLine 绘制带有箭头的直线

arrowedLine函数是OpenCV库中用于在图像上绘制带有箭头的直线的函数。它可以在输入图像上绘制带有箭头的直线段。

以下是arrowedLine函数的C++函数签名：

void arrowedLine(InputOutputArray img, Point pt1, Point pt2, const Scalar& color,
                 int thickness = 1, int line_type = LINE_8, int shift = 0,
                 double tipLength = 0.1)

参数说明：

• img：输入图像，可以是单通道或多通道图像。
• pt1：直线的起点坐标。
• pt2：直线的终点坐标。
• color：绘制直线的颜色，以Scalar对象表示，可以是标量或RGB值。
• thickness：直线的粗细，默认为1。
• line_type：直线的类型，默认为LINE_8，表示8连接线。也可以选择LINE_4（4连接线）或LINE_AA（抗锯齿直线）。
• shift：坐标点的小数位数，默认为0。
• tipLength：箭头的长度与线段长度之比，默认为0.1，表示箭头长度为线段长度的10%。

circle 绘制圆

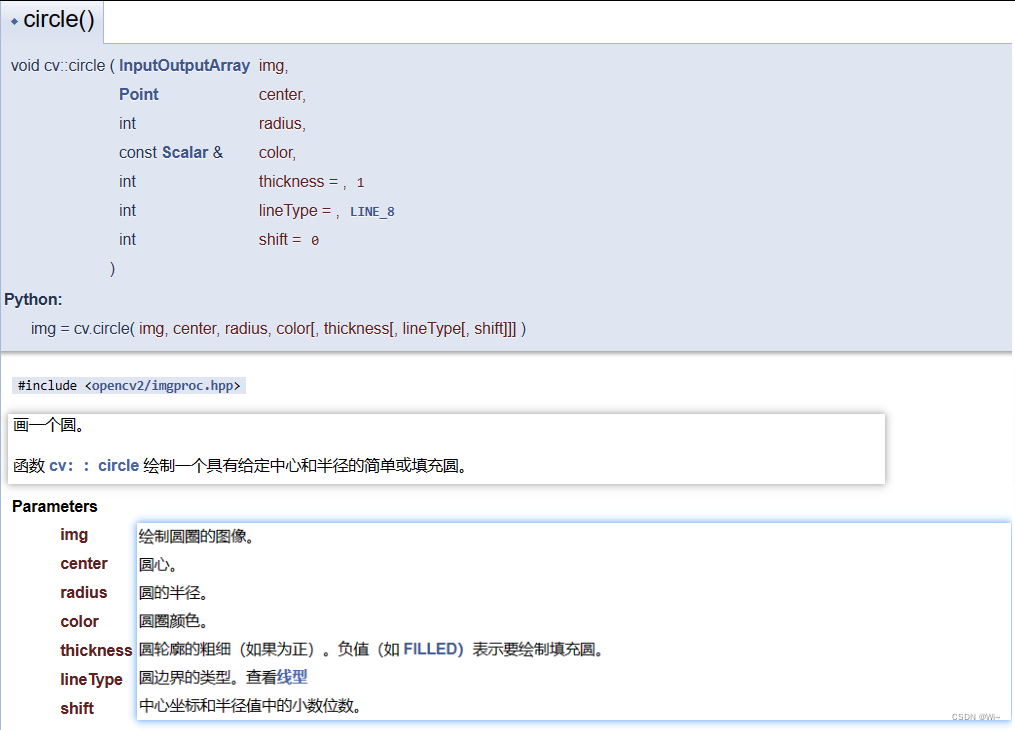
ellipse 绘制椭圆形 ，其他参数如上

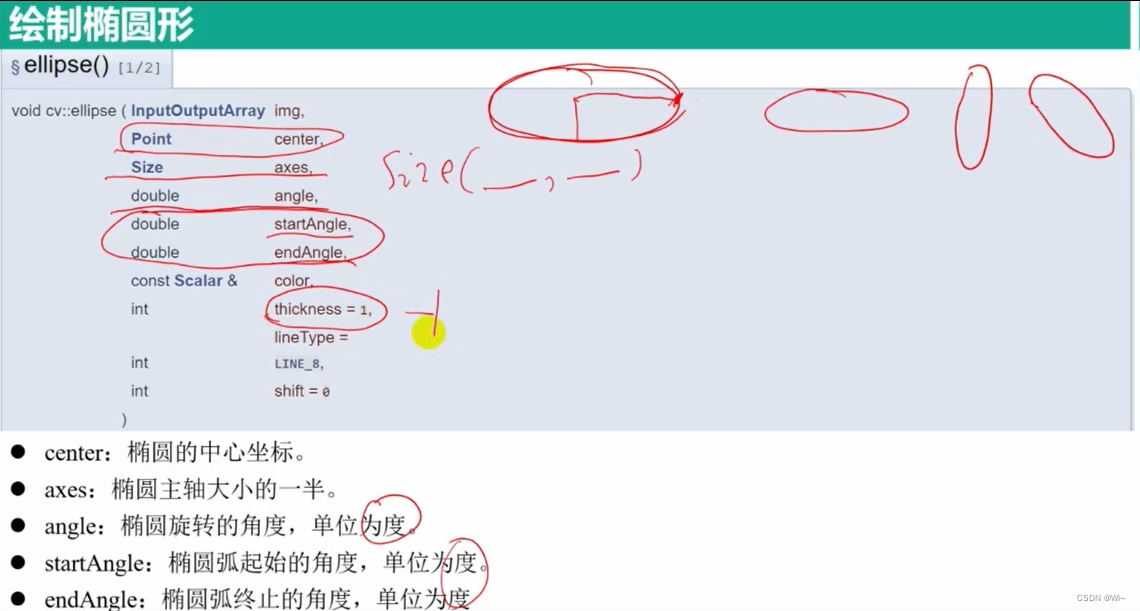
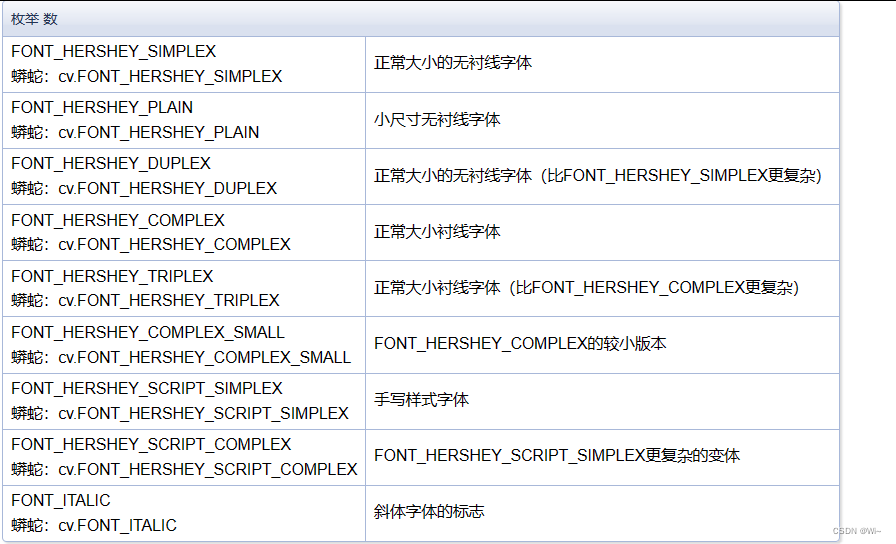
rectangle 绘制矩形 ，其他参数如上

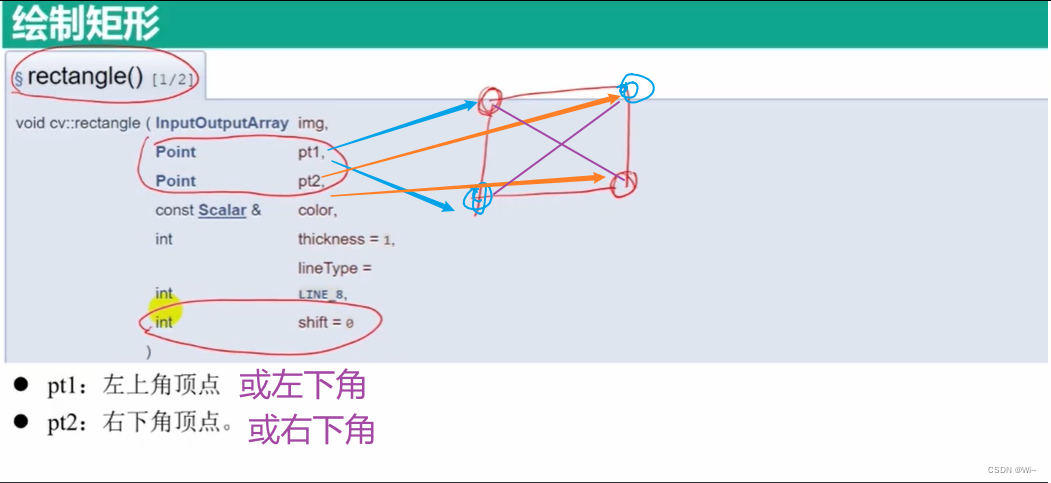
fillPoly 绘制多边形 ，其他参数如上

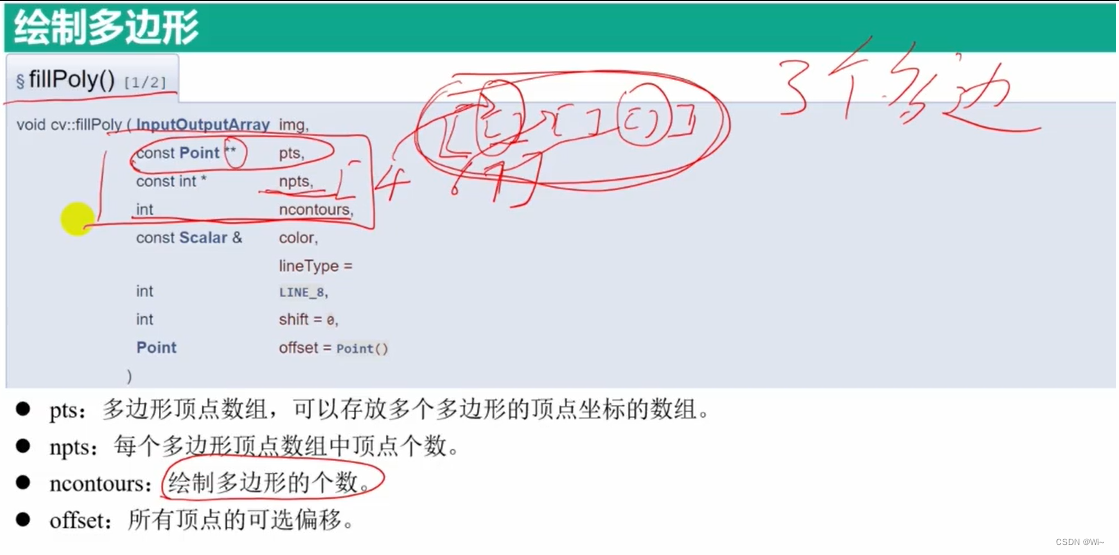
putText 绘制文字 ，其他参数如上

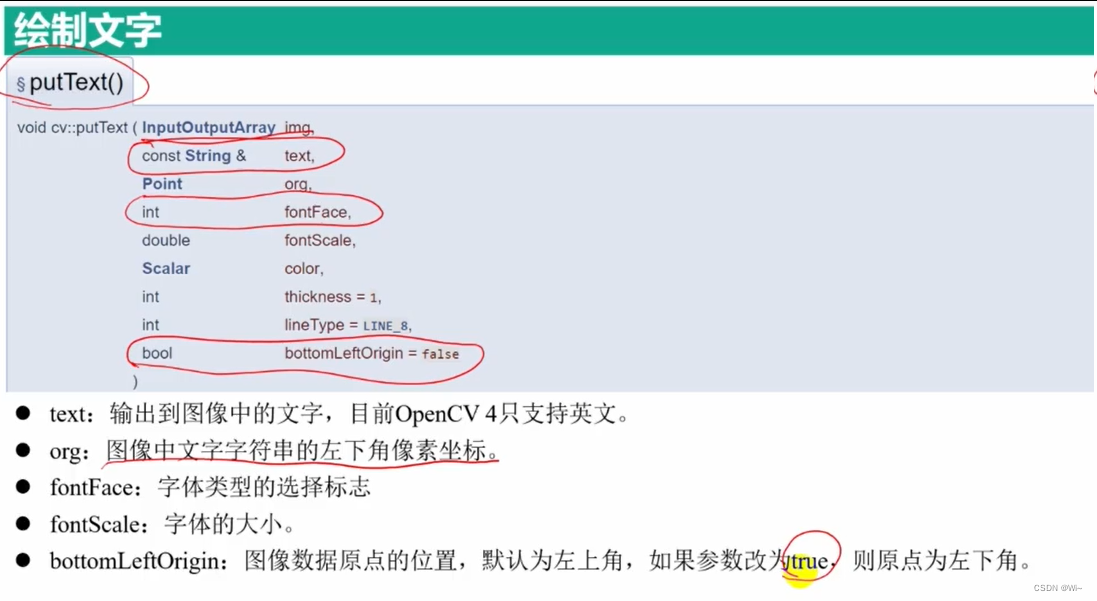
fontFace 标志如下图：

代码演示：

	//创建三通道都为0
	Mat img = Mat::zeros(Size(512, 512), CV_8UC3);
	
	//绘制直线从开始点(100,100)，结束点(200, 100)，颜色(255, 255, 255)
	line(img, Point(100, 100), Point(200, 100), Scalar(255, 255, 255), 2, LINE_4, 0);
	//绘制一个实心圆，圆心(50, 50)，半径25，颜色(255, 255, 255)，-1表示填充
	circle(img, Point(50, 50), 25, Scalar(255, 255, 255), -1);
	//绘制一个空心圆，圆心(100, 50)，半径20，颜色(255, 255, 255)，轮廓宽度为4
	circle(img, Point(100, 50), 20, Scalar(255, 255, 255), 4);

	//绘制椭圆 ，圆心(300, 255)，x半径100，y半径70，椭圆角度0，开始角度0，结束角度210(角度顺时针为正)
	ellipse(img, Point(300, 255), Size(100, 70), 0, 0, 210, Scalar(255, 255, 255), -1);

	//绘制矩形  ，左上角坐标(50, 400)，右下角坐标(100, 450)，颜色(255, 255, 255)，-1表示填充
	rectangle(img, Point(50, 400), Point(100, 450), Scalar(255, 255, 255), -1);
	
	//绘制多边形
	Point pp[2][5];
	pp[0][0] = Point(72, 200);
	pp[0][1] = Point(142, 204);
	pp[0][2] = Point(226, 263);
	pp[0][3] = Point(172, 310);
	pp[0][4] = Point(177, 319);


	pp[1][0] = Point(447, 351);
	pp[1][1] = Point(504, 349);
	pp[1][2] = Point(484, 433);

	//pts变量的生成
	const Point *pts[2] = { pp[0],pp[1] };
	//顶点个数数组的生成
	const int npts[] = { 5,3 };
	//绘制2个多边形
	fillPoly(img, pts, npts, 2, Scalar(255, 255, 255), 8);
	

	//生成文字 
	putText(img, "learn OpenCv 4", Point(100, 130), FONT_HERSHEY_SIMPLEX, 1, Scalar(255, 255, 255));
	putText(img, "learn OpenCv 4", Point(100, 150), FONT_HERSHEY_SIMPLEX, 1, Scalar(255, 255, 255), 1, LINE_4, true);

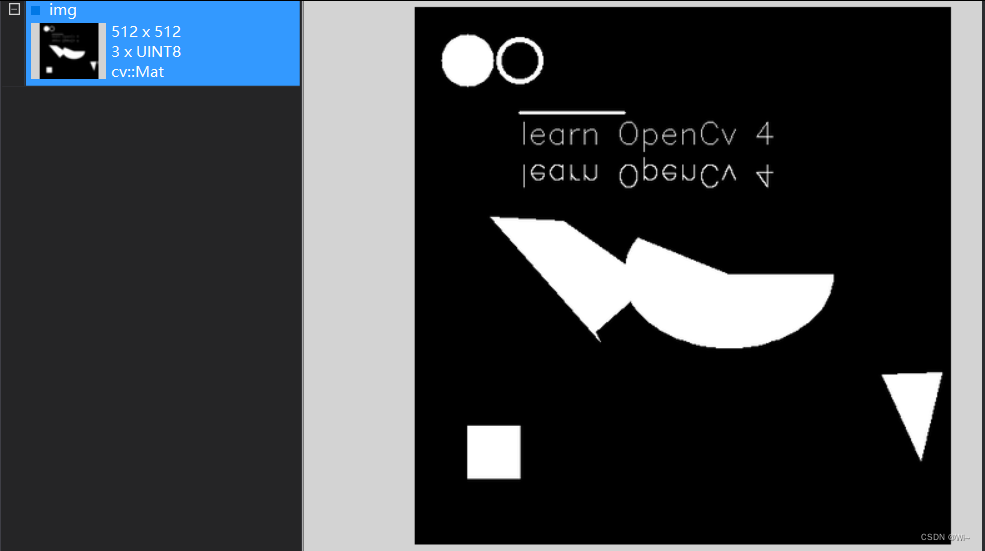
ROI区域截取

Range

Rect_

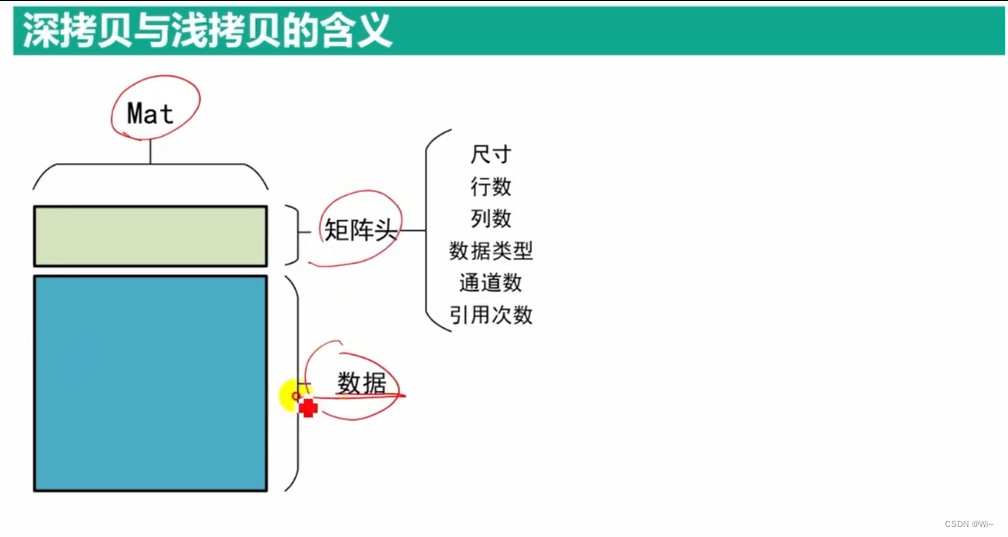
copyTo 深拷贝数据

    浅拷贝：
    Mat a;
    Mat b;
    //把b的头信息复制到a，数据都指向同一个数据
    a = b;


    /*
    浅拷贝是指拷贝了Mat对象的指针和数据头信息，但并没有拷贝数据本身。
    这种拷贝方式通常是通过赋值操作来实现的。浅拷贝后的对象和原始对象共享数据，
    因此当其中一个对象发生变化时，另一个对象也会受到影响。

    深拷贝是指拷贝了Mat对象的数据和数据头信息，生成了一个新的独立对象。
    这种拷贝方式通常是通过clone()函数来实现的。深拷贝后的对象和原始对象是独立的，互相不受影响。

    一般来说，当我们需要对Mat对象进行修改时，应该使用深拷贝，以免原始对象被意外修改。
    而在仅需要读取Mat对象时，使用浅拷贝可以节省内存开销和时间。
    
    clone()和copyTo()是OpenCV中两种不同的复制Mat对象的方法，它们的实现方式不同，
    但都可以用来创建一个独立的Mat对象，使其与原始对象互相独立，互不影响。

    clone()函数用于创建一个独立的Mat对象，它会复制原始对象的所有数据和元数据。
    所以，clone()函数会产生一个完全独立的对象，其内存空间与原始对象的内存空间是不同的。
    这意味着，在复制后，任何对新对象的更改都不会影响原始对象。
    */


    cv::Mat img1 = cv::imread("image.jpg");  // 读取原始图像
    cv::Mat img2 = img1.clone();             // 创建一个独立的Mat对象

    /*copyTo()函数也用于创建一个独立的Mat对象，但它可以将数据复制到一个现有的Mat对象中。
    如果目标Mat对象与原始Mat对象的大小和类型不同，则会自动进行缩放或类型转换。
    copyTo()函数还可以选择复制部分数据，而不是全部数据。
    */


    cv::Mat img1 = cv::imread("image.jpg");       // 读取原始图像
    cv::Mat img2(img1.size(), img1.type());       // 创建一个新的Mat对象
    img1.copyTo(img2);                            // 将img1的数据复制到img2中

    /*
    因此，如果需要创建一个完全独立的Mat对象，可以使用clone()函数，
    而如果需要将数据复制到现有的Mat对象中，则可以使用copyTo()函数。
    无论使用哪种方法，都可以确保生成的新对象是独立的，不会影响原始对象。
    */

    

代码演示：

Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");
	
	Mat orange = imread("D:/OpenCV4.5.1/opencv/sources/samples/data/orange.jpg");
	if (img.empty() || orange.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}

	Mat ROI1, ROI2, ROI2_copy, mask, img2, img_copy;

	//重置图像orange像素到mask大小(200, 200)
	resize(orange, mask, Size(200, 200));

	//浅拷贝
	img2 = img;
	 //深拷贝的两种方式
	img.copyTo(img_copy);

	//两种在图中截取ROI区域的方式:左上角坐标（150, 150），宽200，高200
	Rect rect(150, 150, 200, 200);
	//抠图
	ROI1 = img(rect);
	ROI2 = img(Range(300, 400), Range(300, 400));

	img(Range(300, 400), Range(300, 400)).copyTo(ROI2_copy);

	//ROI1 如果是已存在的矩阵大小和mask矩阵大小一致，直接把数据复制到ROI1原来的内存，
	//不一致的话，ROI1重新分配内存，不会把mask数据复制到ROI1原来的内存。
	mask.copyTo(ROI1);
	//img 和img2 和 ROI1 和 ROI2 数据都是在同一个内存中
	


	Mat clone1;
	//克隆数据  img和clone1所有数据都一样，但是两个内存地址不一样
	clone1 = img.clone();

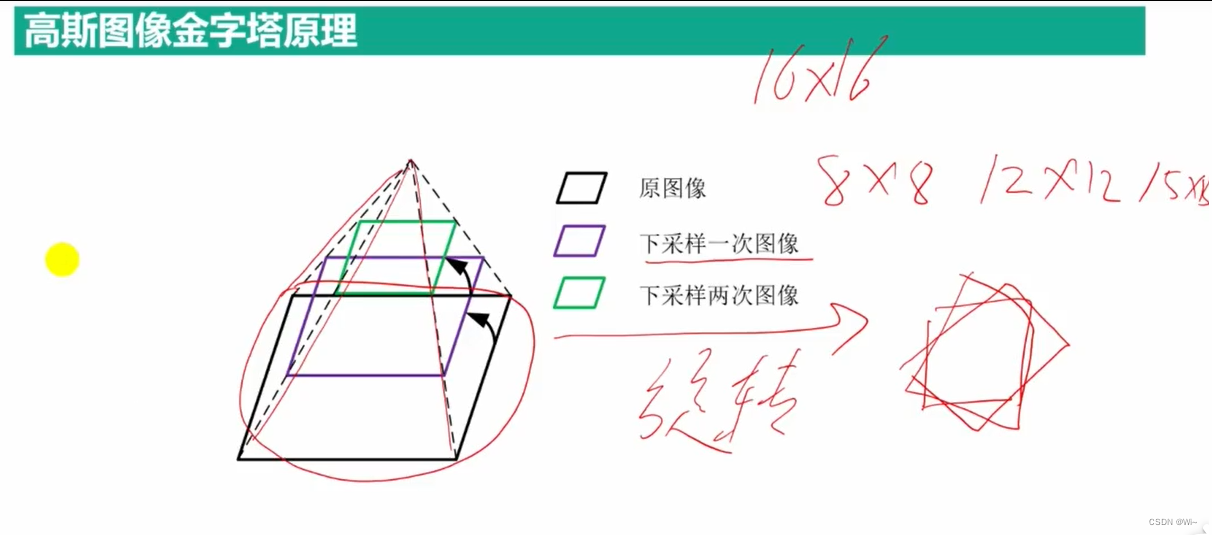
高斯图像金字塔，拉普拉斯图像金字塔

pyrDown 下采样

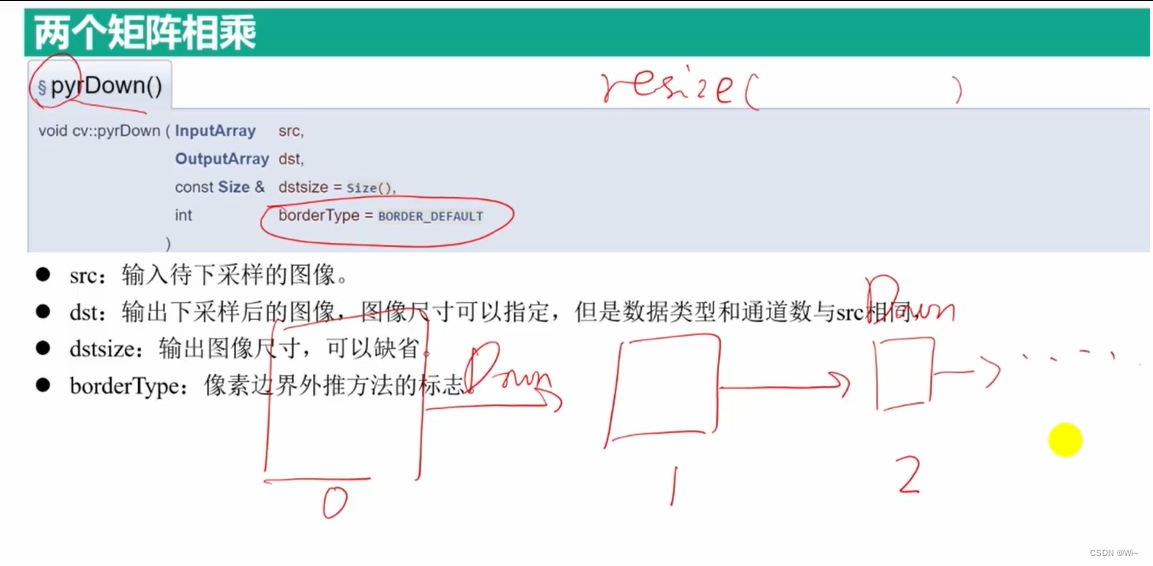
pyrUp 上采样

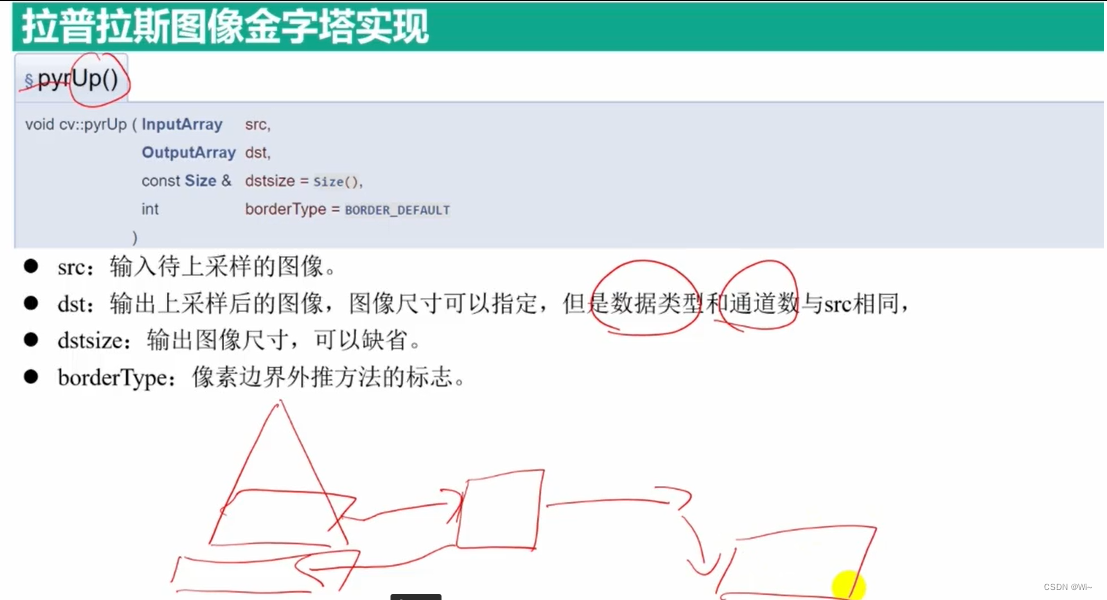
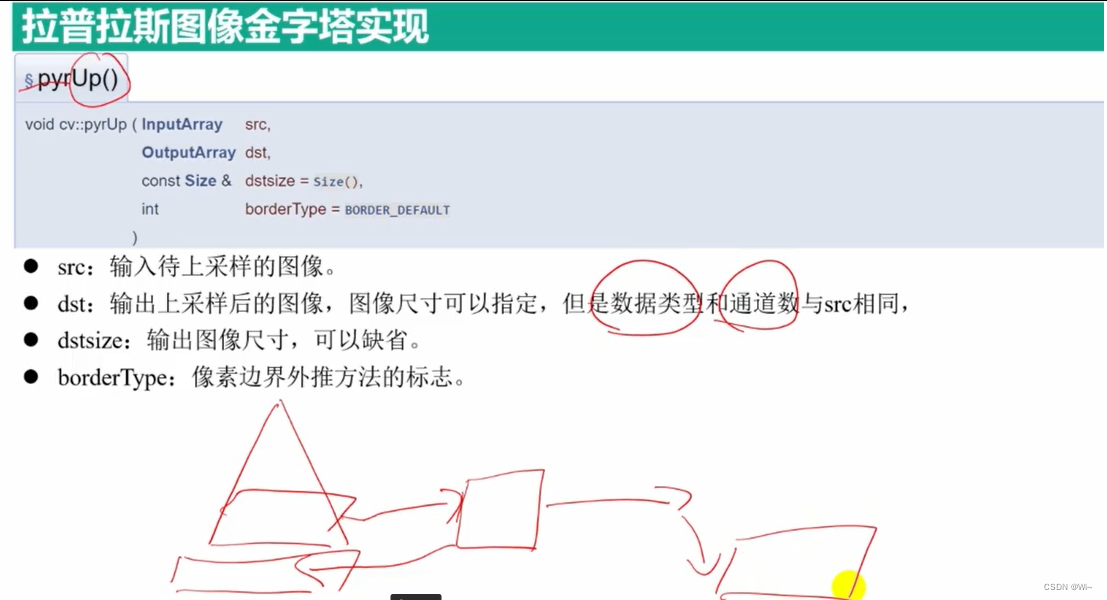
resize、pyrUp 和 pyrDown 图像金字塔（高斯金字塔、拉普拉斯金字塔）与尺寸缩放（向上采样、向下采样）

    resize 函数，最直接的方法。
    pyrUp 和 pyrDown 函数，即图像金字塔相关的两个函数，对图像进行向上采样和向下采样的操作。

pyrUp 和 pyrDown 其实和专门用于放大缩小图像尺寸的 resize 在功能上差不多，批着图像金字塔的皮，说白了还是对图像进行放大和缩小操作。

图像金字塔

    一幅图像的金字塔是一系列以金字塔形状排列，分辨率逐渐降低且源于同一张原始图的图像集合。
    金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。层级越高，图像越小，分辨率越低。
    图像金字塔是图像中多尺度表达的一种，最初用于机器视觉和图像压缩，
    最主要功能用于图像分割，是一种以多分辨率来解释图像的有效但概念简单的结构。

向上、向下采样
图像金字塔中的向上和向下采样分别通过 pyrUp 和 pyrDown 实现。
这里的向上向下采样，是针对图像的尺寸而言的（和金字塔的方向相反），
向上就是图像尺寸加倍，向下就是图像尺寸减半。但需要注意的是，pyrUp 和 pyrDown 不是互逆的。

    对于 pyrUp，图像首先在每个维度上扩大为原来的两倍，新增的行和列（偶数行和列）以 0 填充。
    然后用指定的滤波器进行卷积（实际上是一个在每个维度上都扩大为原来两倍的过滤器）去估计”丢失“像素的近似值。
    对于 pyrDown，我们先要用高斯核对图像进行卷积，然后删除所有偶数行和偶数列，新的到的图像面积就会变成源图像的四分之一。

高斯金字塔
高斯金字塔是通过高斯平滑和亚采样获得的一系列采样图像。

    向下采样方法：① 对图像进行高斯内核卷积；② 将所有偶数行和列去除。
    向上采样方法：① 将图像在每个方向上扩大为原来的两倍，新增的行和列以 0 填充；
    ② 使用原先同样的内核（乘以 4）与放大后的图像卷积，获得”新增像素“的近似值。
    在缩放过程中已经丢失了一些信息，如果想在缩放过程中减少信息的丢失，就需要用到拉普拉斯金字塔。

拉普拉斯金字塔
拉普拉斯金字塔是通过源图像减去先缩小再放大的图像的一系列图像构成。

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");

	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}
	vector<Mat> Guass;
	int level = 3;
	//图从大到小保存到vector
	Guass.push_back(img);
	for (int i = 0; i < level; i++)
	{
		Mat guass;
		pyrDown(Guass[i], guass);
		Guass.push_back(guass);
	}

	vector<Mat> Lap;
	//图从小到到大保存到vector
	for (int i = Guass.size() - 1; i > 0; i--)
	{
		Mat lap, upGuass;
		if (i == Guass.size() - 1)
		{
			Mat down;
			pyrDown(Guass[i], down);
			pyrUp(down, upGuass);
			lap = Guass[i] - upGuass;
			Lap.push_back(lap);

		}
		pyrUp(Guass[i], upGuass);
		lap = Guass[i - 1] - upGuass;
		Lap.push_back(lap);
	}

	for (int i = 0; i < Guass.size(); i++)
	{
		string name = to_string(i);
		imshow("G" + name, Guass[i]);
		imshow("L" + name, Lap[Guass.size()-1-i]);
	}

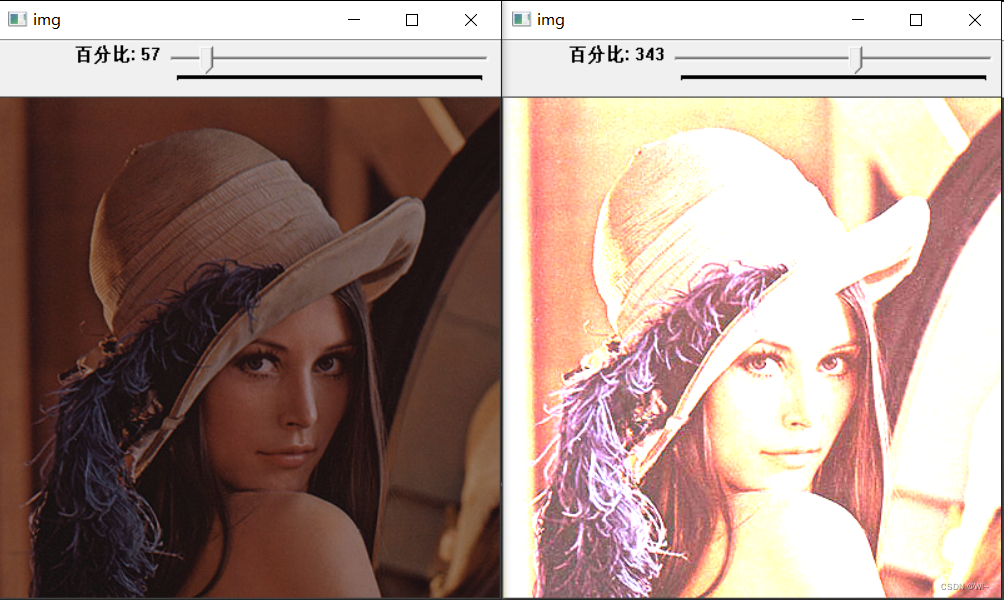
创建滑动条

createTrackbar

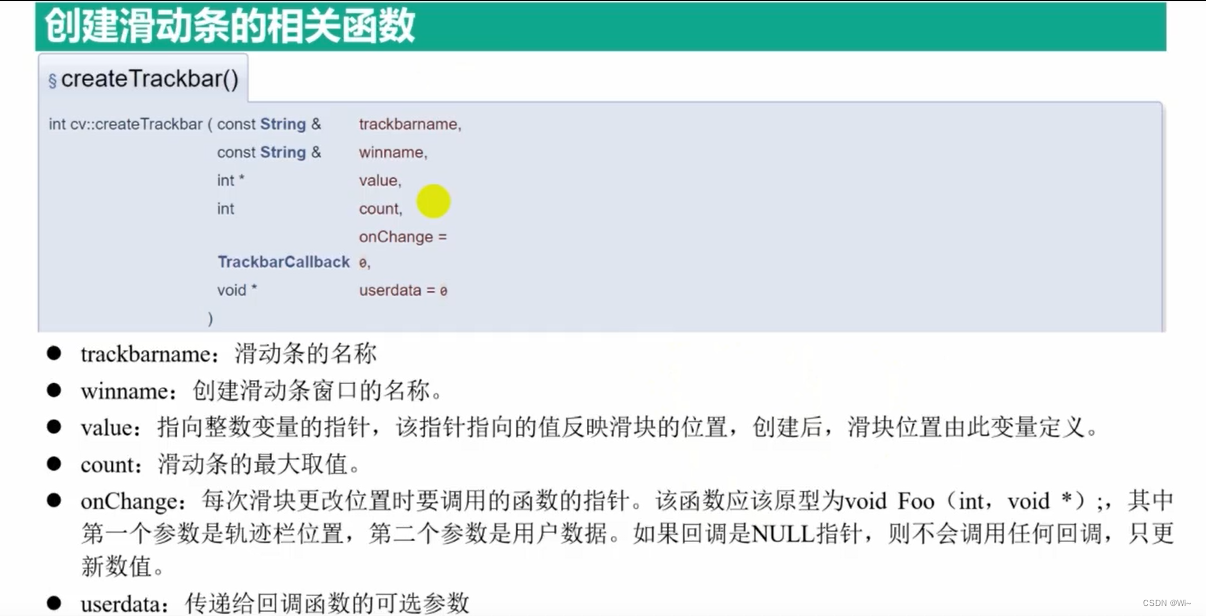
回调函数原型：
typedef void (*TrackbarCallback)(int pos, void* userdata);

代码演示

//声明
void callBack(int value, void *);

int main()
{
		Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");

		if (img.empty())
		{
			cout << "图像打开失败。。。" << endl;
			return -1;
		}

		namedWindow("img");
		imshow("img", img);
		int value = 100;

		createTrackbar("百分比", "img", &value, 600, callBack, &img);

	
	waitKey(0);
	return 0;
}

//回调函数
void callBack(int value, void *data)
{
	Mat img = *(Mat*)data;
	float a = value / 100.0;

	imshow("img", img * a);
}

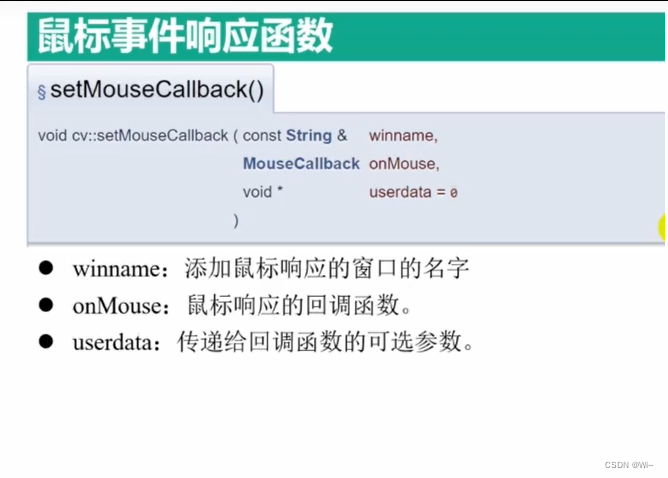
鼠标事件响应

setMouseCallback 鼠标响应事件函数

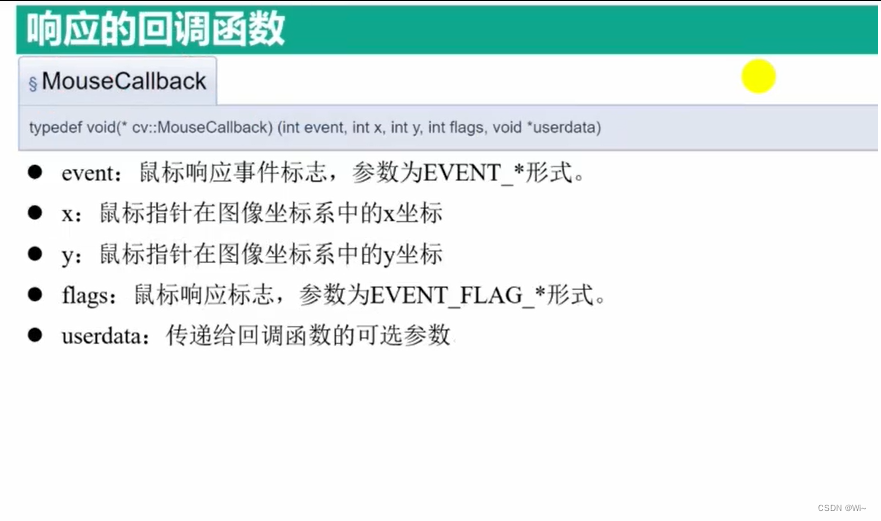
MouseCallback 鼠标回调函数

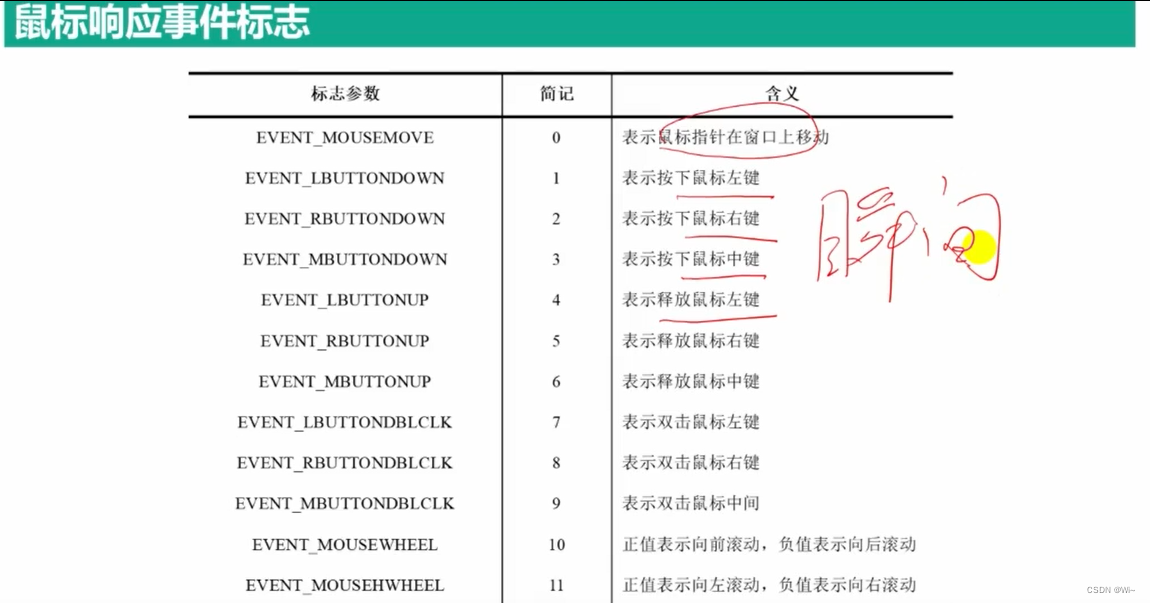
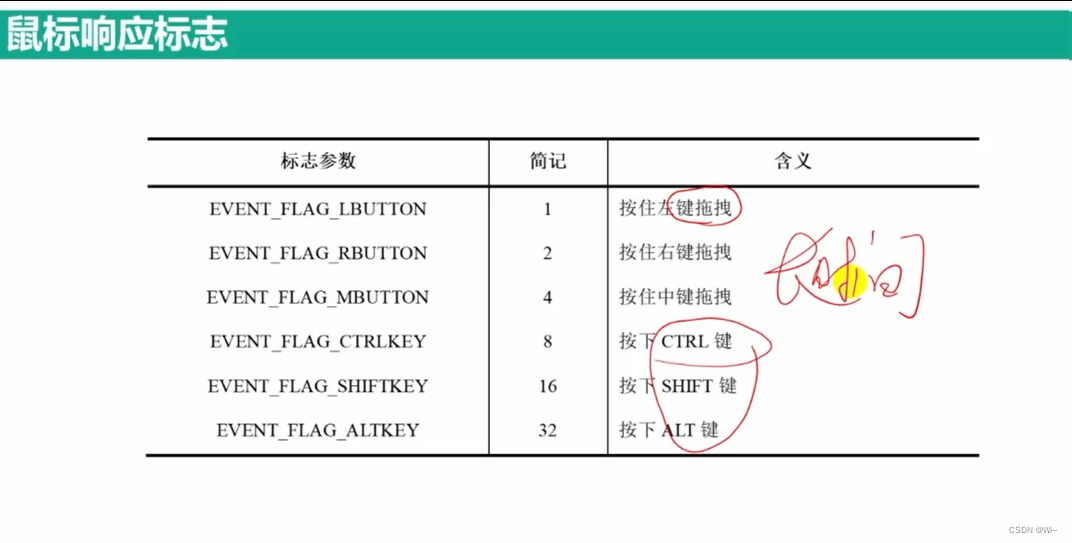
代码演示：

//回调函数
void mouseCB(int evnet,int x,int y,int flags,void *);
//全局变量
Point perPoint;
int main()
{

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");
	Mat imgPoint;
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}

	img.copyTo(imgPoint);
	string str1 = "img";
	imshow(str1, img);
	setMouseCallback(str1, mouseCB, &img);
		
		
	
	waitKey(0);
	return 0;
}

//回调函数
void mouseCB(int event, int x, int y, int flags, void *data)
{
	Mat img = *(Mat*)data;

	//单击右键
	if (event == EVENT_RBUTTONDOWN)
	{
		cout << "点击鼠标左键才可以绘制轨迹" << endl;
	}
	//单击左键，输出坐标
	if (event == EVENT_LBUTTONDOWN)
	{
		//记录开始
		perPoint = Point(x, y);
		cout << "轨迹其实坐标: " <<perPoint<< endl;
	}
	//鼠标必须移动 并且 鼠标长按左键   flags & EVENT_FLAG_LBUTTON   在这里类似 flags == EVENT_FLAG_LBUTTON
	if (event == EVENT_MOUSEMOVE && (flags & EVENT_FLAG_LBUTTON))
	{
		Point pt(x, y);
		//划线
		line(img, perPoint, pt, Scalar(255, 255, 255), 3);
		perPoint = pt;
		imshow("img", img);
	}
}

图像直方图的绘制

calcHist

hist保存的信息：

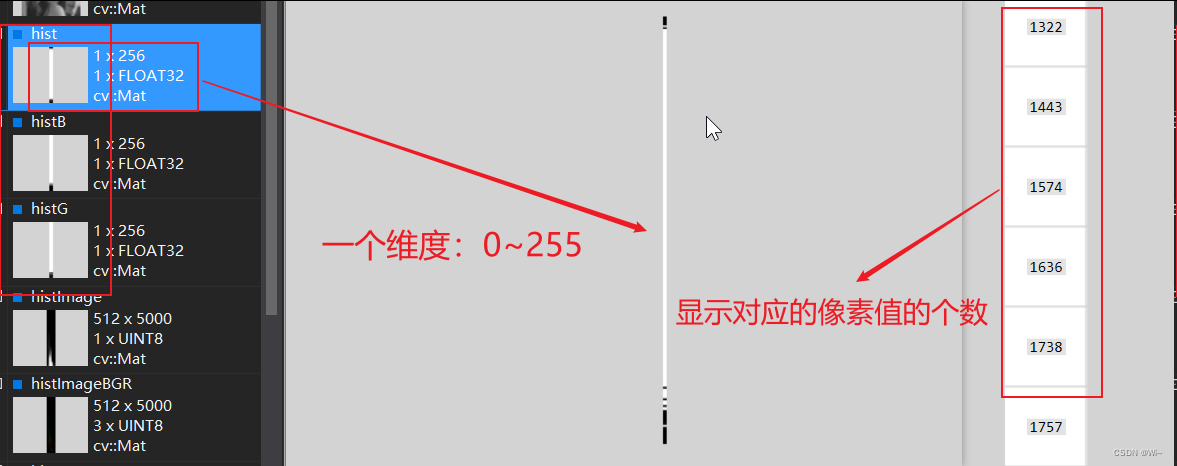
代码演示：

    Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg");
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}

	Mat gray;
	//bgr 2 gray
	cvtColor(img, gray, COLOR_BGR2GRAY);

	//设置提取直方图的相关变量
	//用于存放直方图计算结果
	Mat hist;
	//通道索引
	const int channels[1] = { 0 };
	//直方图的维度，其实就是像素灰度值的最大值
	const int bins[1] = { 256 };
	float inRanges[2] = { 0,255 };
	//像素灰度值范围
	const float*ranges[1] = { inRanges };
	//计算图像直方图
	calcHist(&gray,1,channels,Mat(),hist,1,bins,ranges );

	//绘制直方图
	int hist_w = 512;
	int hist_h = 5000;
	int width = 2;
	Mat histImage = Mat::zeros(hist_h, hist_w, CV_8UC1);
	for (int i = 0; i < hist.rows; i++)
	{

		cout << "左上角: " << Point(width*(i), hist_h - 1) << endl;
		cout << "有下角: " << Point(width*(i + 1), hist_h - 1 - hist.at<float>(i)) << endl;
		rectangle(histImage, Point(width*(i), hist_h-1), Point(width*(i+1), hist_h - 1 - hist.at<float>(i)), Scalar(255, 255, 255), -1);//绘制直方图
	}
	namedWindow("img", WINDOW_NORMAL);
	imshow("img", histImage);

	{
		//设置提取直方图的相关变量
		//用于存放直方图计算结果
		Mat histB, histG, histR;
		//通道索引
		const int channels[1] = { 0 };
		//直方图的维度，其实就是像素灰度值的最大值
		const int bins[1] = { 256 };
		float inRanges[2] = { 0,255 };
		//像素灰度值范围
		const float*ranges[1] = { inRanges };

		Mat imgs[3];
		//分割三通道图像 按照BGR形式分割
		split(img, imgs);

		//计算图像直方图
		calcHist(&imgs[0], 1, channels, Mat(), histB, 1, bins, ranges);
		calcHist(&imgs[1], 1, channels, Mat(), histG, 1, bins, ranges);
		calcHist(&imgs[2], 1, channels, Mat(), histR, 1, bins, ranges);
		//绘制直方图
		int hist_w = 512;
		int hist_h = 5000;
		int width = 2;
		//创建三通道背景
		Mat histImageBGR = Mat::zeros(hist_h, hist_w, CV_8UC3);
		for (int i = 1; i < 256; i++)
		{
			line(histImageBGR, Point(width*(i - 1), hist_h - cvRound(histB.at<float>(i - 1))), Point(width*(i), hist_h - cvRound(histB.at<float>(i))), Scalar(255, 0, 0), width);//绘制直方图
			line(histImageBGR, Point(width*(i - 1), hist_h - cvRound(histG.at<float>(i - 1))), Point(width*(i), hist_h - cvRound(histG.at<float>(i))), Scalar(0, 255, 0), width);//绘制直方图
			line(histImageBGR, Point(width*(i - 1), hist_h - cvRound(histR.at<float>(i - 1))), Point(width*(i), hist_h - cvRound(histR.at<float>(i))), Scalar(0, 0, 255), width);//绘制直方图

		}
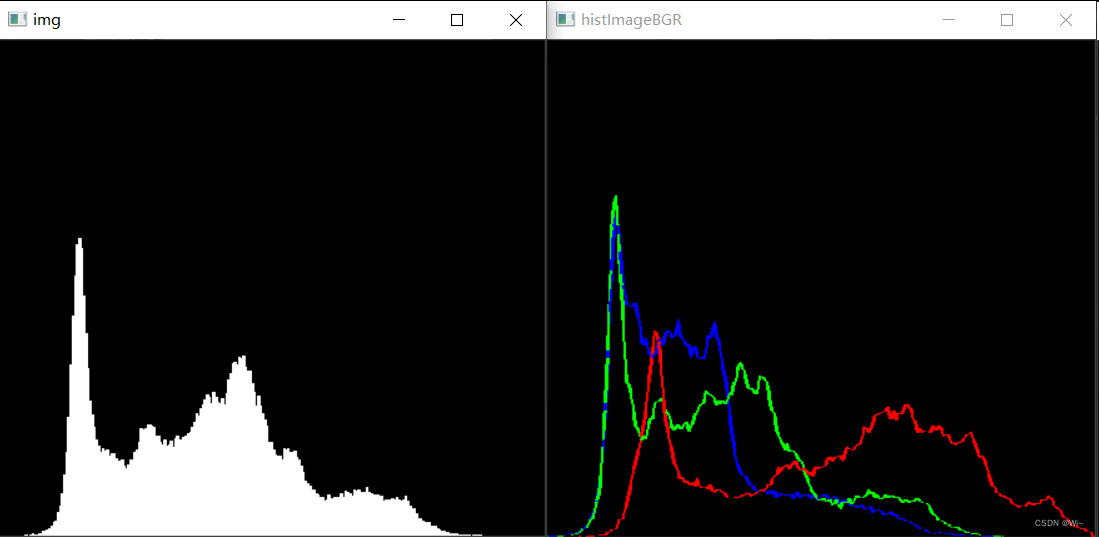
		namedWindow("histImageBGR", WINDOW_NORMAL);
		imshow("histImageBGR", histImageBGR);
	}

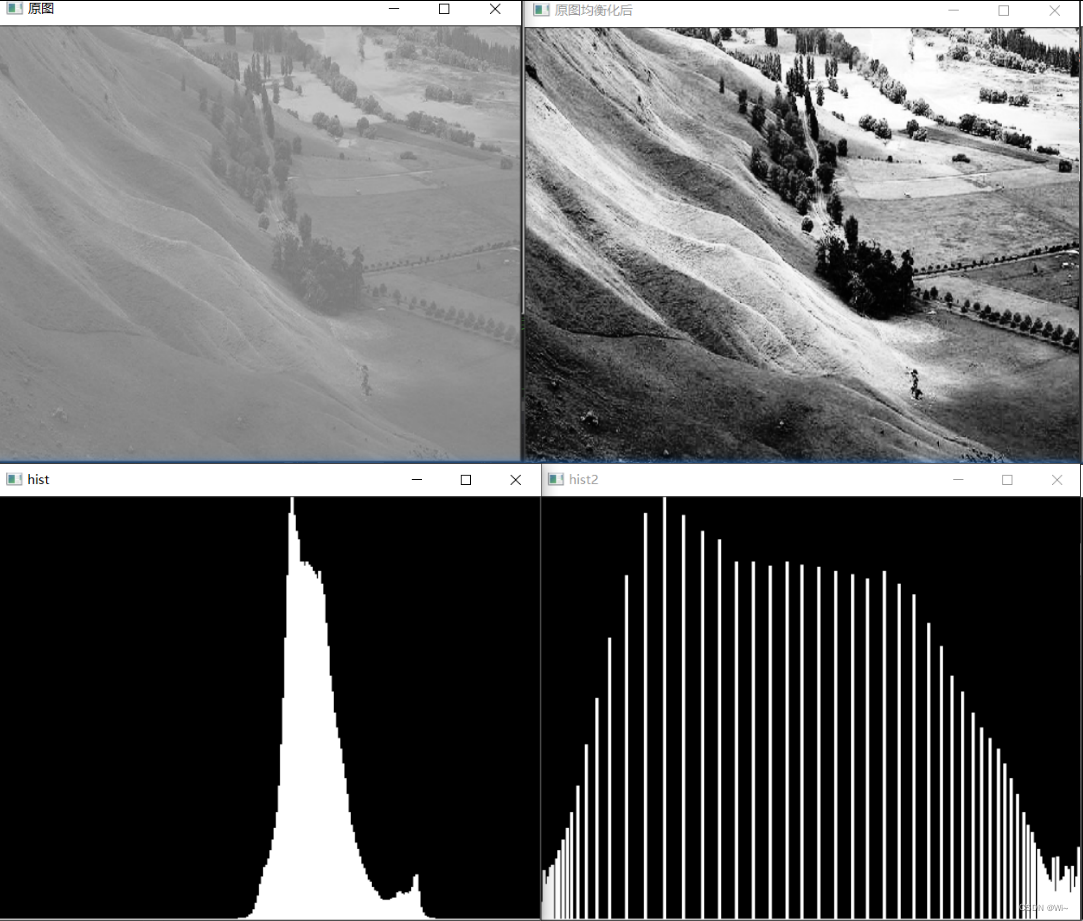
直方图均衡化

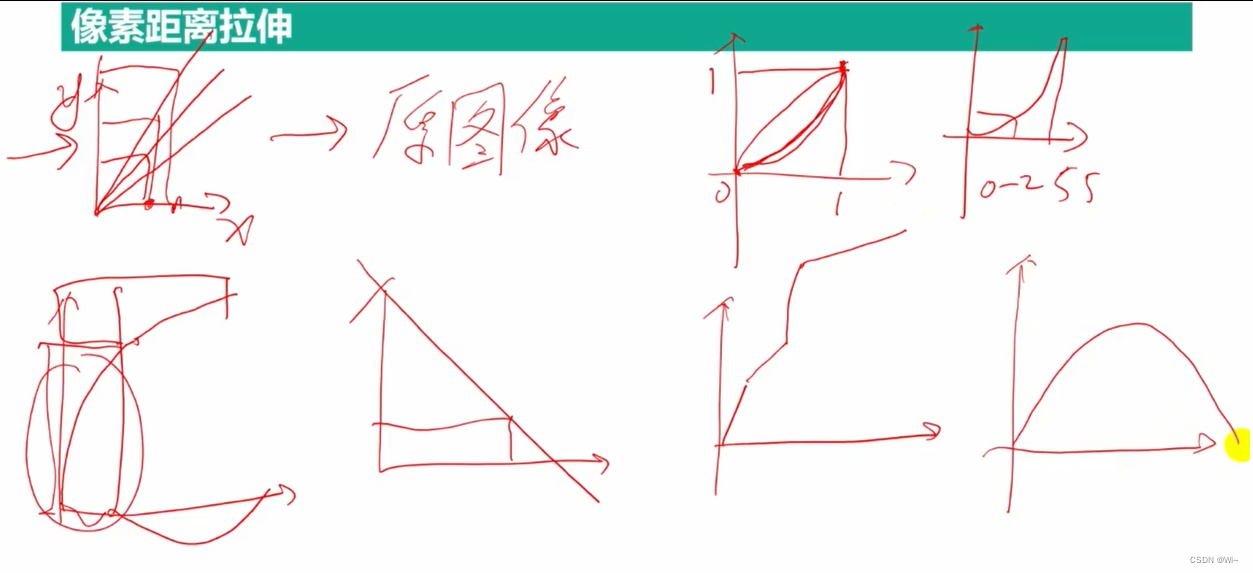
equalizeHist

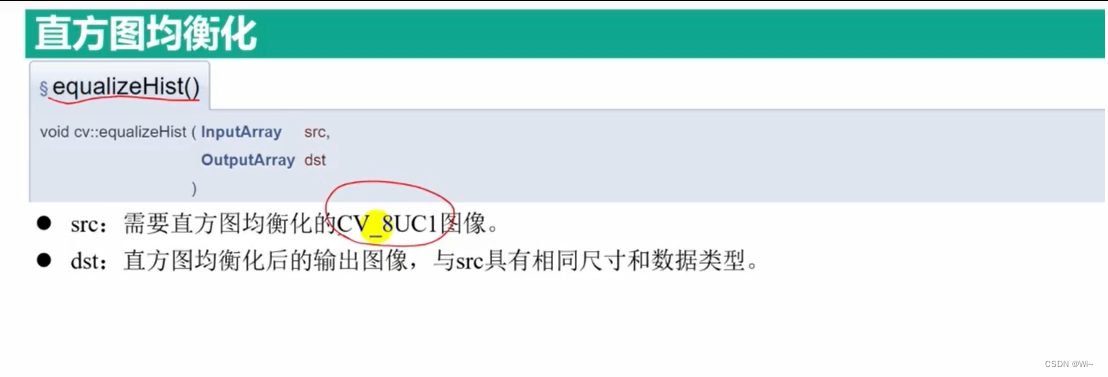
直方图均衡化的定义：将随机分布的直方图修改为均匀分布的直方图，其实质是对图像进行非线性拉伸，重新分配图像像元值，使一定灰度范围内的像元的数量大致相等。

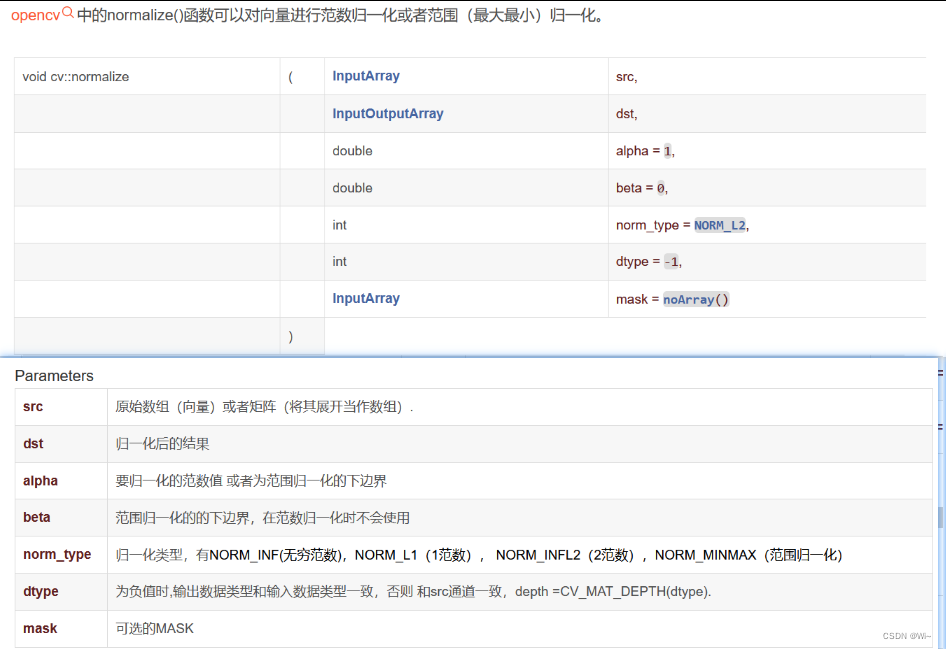
normalize 数据归一化

归一化就是要把需要处理的数据经过处理后（通过某种算法）限制在你需要的一定范围内。

首先归一化是为了后面数据处理的方便，其次是保证程序运行时收敛加快。
归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布，归一化在某个区间上是统计的坐标分布。
归一化有同一、统一和合一的意思。

归一化的目的，是使得没有可比性的数据变得具有可比性，同时又保持相比较的两个数据之间的相对关系，
如大小关系；或是为了作图，原来很难在一张图上作出来，归一化后就可以很方便的给出图上的相对位置等。

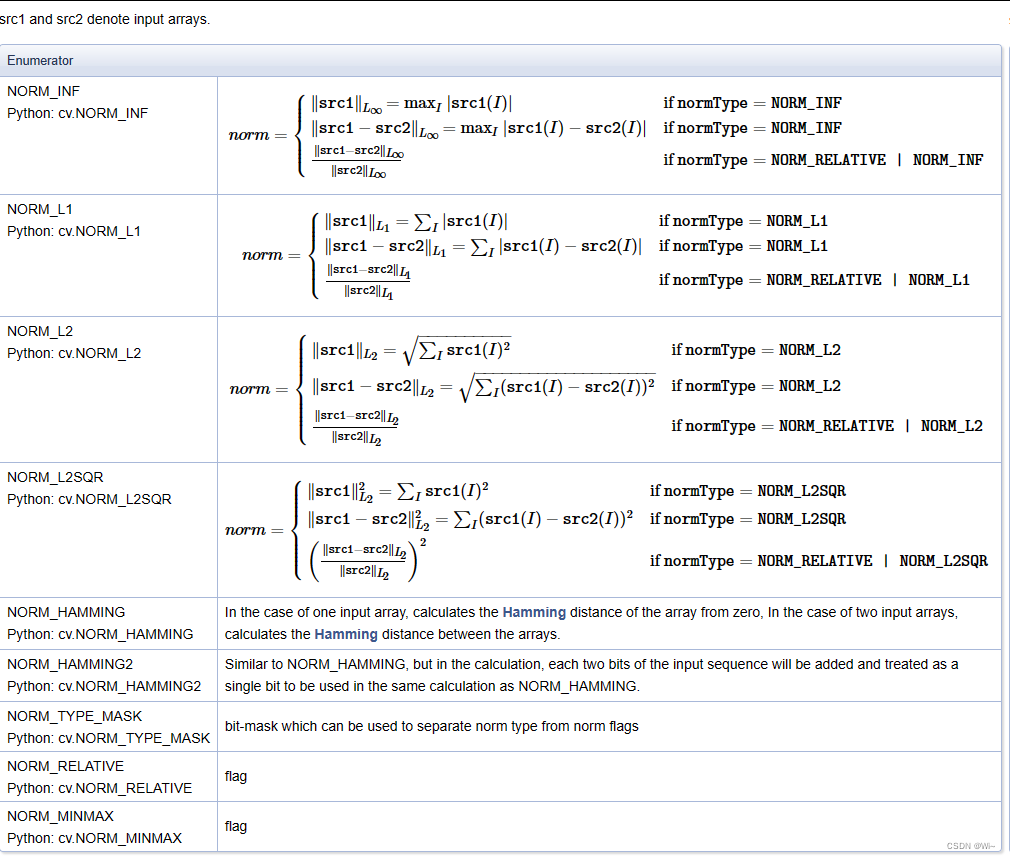
norm_type如下：

注意：   对于多通道数据，normalize()函数直接将其按内存中的顺序展开为数组，及当作一个向量进行处理。

实例：
 vector<double> positiveData = { 2.0, 8.0, 10.0 };
 vector<double> normalizedData_l1, normalizedData_l2, normalizedData_inf, normalizedData_minmax;
范数归一化：
1.    1范数：

 // sum(numbers) = 20.0 //2.0+8.0+10.0 

 // 2.0 0.1 (2.0/20.0)

 // 8.0 0.4 (8.0/20.0)

 // 10.0 0.5 (10.0/20.0)

 normalize(positiveData, normalizedData_l1, 1.0, 0.0同上最终归一化的值为单位向量的每个值乘以参数要归一化的范数值alpha。, NORM_L1);

直接求和后算出每一个算数比上总和的比值，加起来总为1。这里要归一化的范数值为1.0，
所求出的比值即为最后归一化后的值，若归一化范数值alpha为2.0，
则每个比值分别乘以2.0即得到最后归一化后的结果为0.2, 0.8, 1.0，以此类推。

2.   2范数：


 // Norm to unit vector: ||positiveData|| = 1.0
//模长 = ((2.0)²+(8.0)²+(10.0)²)的结果开根号 = 12.961481396815720461931934872176
 // 2.0 0.15   = 2 / 12.961481396815720461931934872176

 // 8.0 0.62    = 8 / 12.961481396815720461931934872176

 // 10.0 0.77    = 10 / 12.961481396815720461931934872176

 normalize(positiveData, normalizedData_l2, 1.0, 0.0, 
 NORM_L2);

即将该向量归一化为单位向量，每个元素值除以该向量的模长。同上最终归一化的值为单位向量的每个值乘以参数要归一化的范数值alpha。

3.   无穷范数


 // Norm to max element

 // 2.0 0.2 (2.0/10.0)

 // 8.0 0.8 (8.0/10.0)

 // 10.0 1.0 (10.0/10.0)

 normalize(positiveData, normalizedData_inf, 1.0, 0.0, 
 NORM_INF);

每个值除以最大值来进行无穷范数归一化。同上最终归一化的值为单位向量的每个值乘以参数要归一化的范数值alpha。


4:范围
NORM_MINMAX

normalize函数中的norm_type参数表示归一化的方法，NORM_MINMAX表示使用最小值和最大值归一化。具体来说，对于输入的数组src，
该方法会通过下面的公式对其进行归一化：

dst(x,y) = (src(x,y) - minVal) * (beta - alpha) / (maxVal - minVal) + alpha

其中，minVal和maxVal分别为src数组中的最小值和最大值，alpha和beta为指定的下限和上限。在归一化过程中，
src数组中的所有元素都会被映射到指定的范围内。因此，使用NORM_MINMAX方法可以将图像的像素值归一化到指定的范围内，便于显示和后续处理。

代码演示：

//归一化并绘制直方图函数
void drawHist(Mat &hist, int type, string name)
{
	//绘制直方图
	int hist_w = 512;
	int hist_h = 400;
	int width = 2;
	Mat histImage = Mat::zeros(hist_h, hist_w, CV_8UC1);

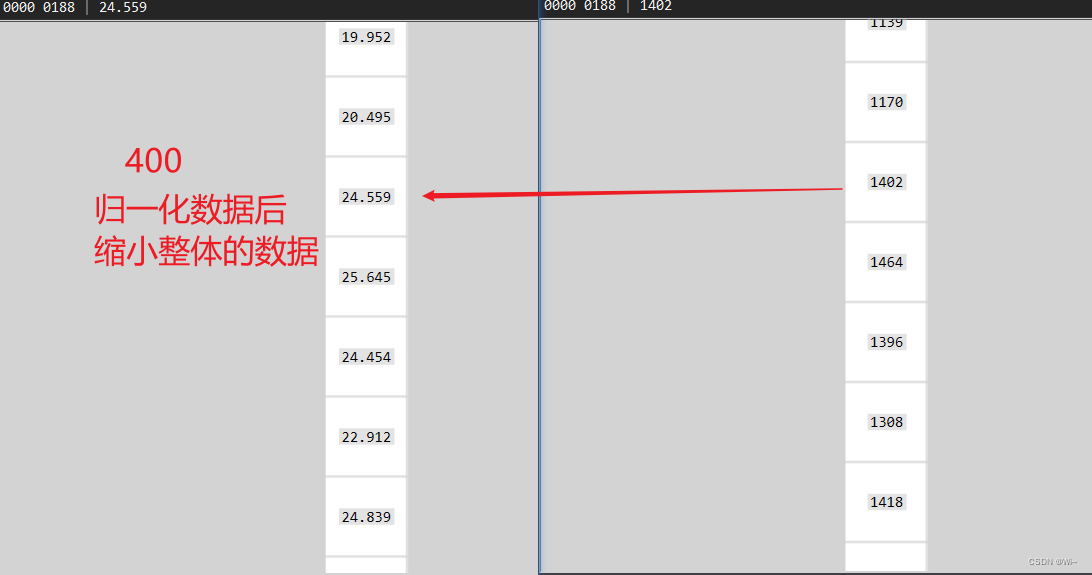
	//直方图hist数据归一化  (这里归hist_h = 400化)
	normalize(hist, hist, hist_h, 0, type);

	for (int i = 0; i < hist.rows; i++)
	{
		rectangle(histImage, Point(width*(i), hist_h - 1), Point(width*(i + 1), cvRound(hist_h - 1 - hist.at<float>(i))), Scalar(255, 255, 255), -1);//绘制直方图
	}
	imshow(name, histImage);
}
int main()
{

	Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/Snipaste_2023-04-05_17-29-56shangu.png");
	if (img.empty())
	{
		cout << "图像打开失败。。。" << endl;
		return -1;
	}

	Mat gray, hist, hist2;
	//bgr 2 gray
	cvtColor(img, gray, COLOR_BGR2GRAY);

	Mat equalImg;
	//将图像直方图均衡化  必须是单通道
	equalizeHist(gray,equalImg);

	//通道索引
	const int channels[1] = { 0 };
	//直方图的维度，其实就是像素灰度值的最大值
	const int bins[1] = { 256 };
	float inRanges[2] = { 0,255 };
	//像素灰度值范围
	const float*ranges[1] = { inRanges };
	//计算图像直方图
	calcHist(&gray, 1, channels, Mat(), hist, 1, bins, ranges);
	calcHist(&equalImg, 1, channels, Mat(), hist2, 1, bins, ranges);

	drawHist(hist, NORM_INF, "hist");
	drawHist(hist2, NORM_INF, "hist2");
	
	namedWindow("原图", WINDOW_NORMAL);
	namedWindow("原图均衡化后", WINDOW_NORMAL);
	imshow("原图", gray);
	imshow("原图均衡化后", equalImg);
	
	waitKey(0);
	return 0;
}