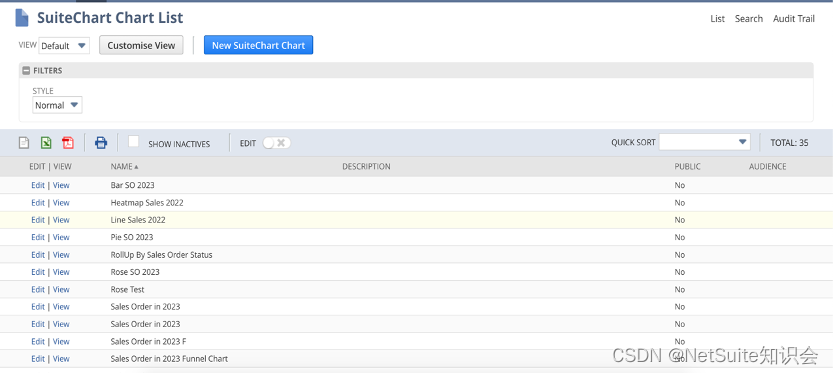
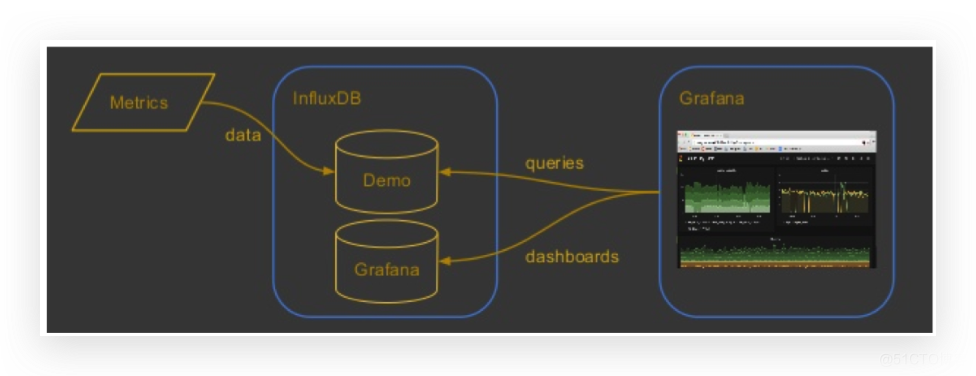
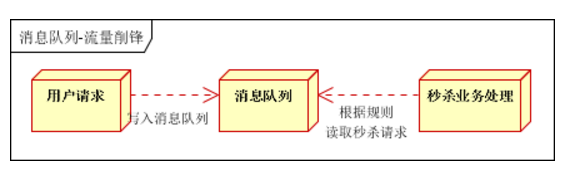
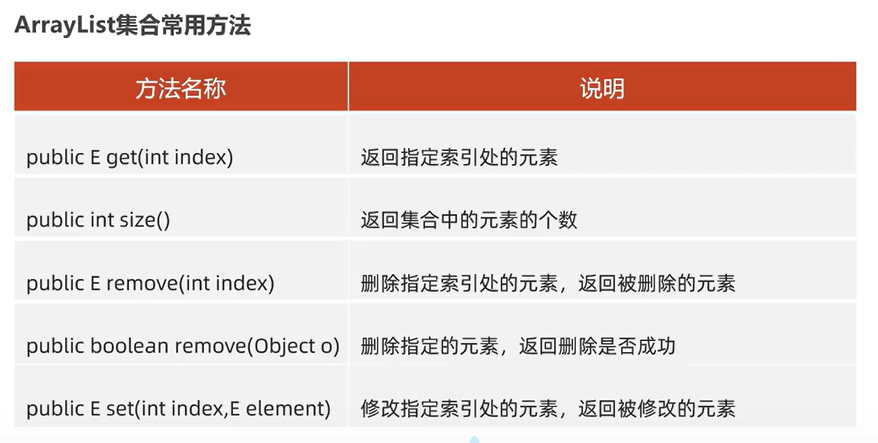
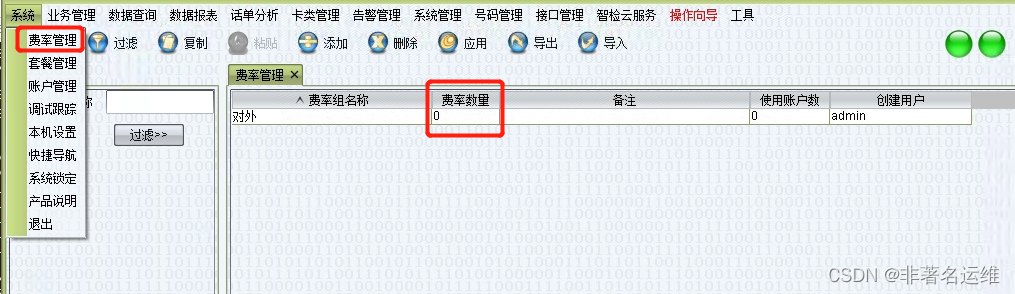
一、说明
Pole and polar 对于几何学,是普遍的概念。可能高中就学过,问题是在双曲几何又用到这个概念,因此,这里再次强调理解这个概念 。为后边学习双曲几何扫清障碍。
二、基本概念
在几何学中,极点和极线分别是相对于给定圆锥截面具有唯一倒数关系的点和线。
给定圆中的极点往复运动是将平面中的每个点转换为它的极线,并将平面中的每条线转换为它的极点。总之,极点和极线是一对二元关系。总是伴随出现的。
2.1 一般圆锥曲线的极点与极线方程
对于任意圆锥曲线(圆,椭圆,抛物线,双曲线)

三、圆的极点和极点
3.1 P在圆外
令 P 为圆内或圆外的任意一点。画任何通过 P 的弦 AB 和 CD。如果圆的过P切线的切点S-S‘在 A 和 B 处相交于 Q,则 Q 的轨迹称为 P 相对于圆的极线,P 称为极点,如果切点连线SS‘交圆在C和D处相交于Q',则直线QQ'就是以P为极点的极线。
其中不变的性质是:AQ*BP=QB*AP;或CQ’*DP=Q'D*CP
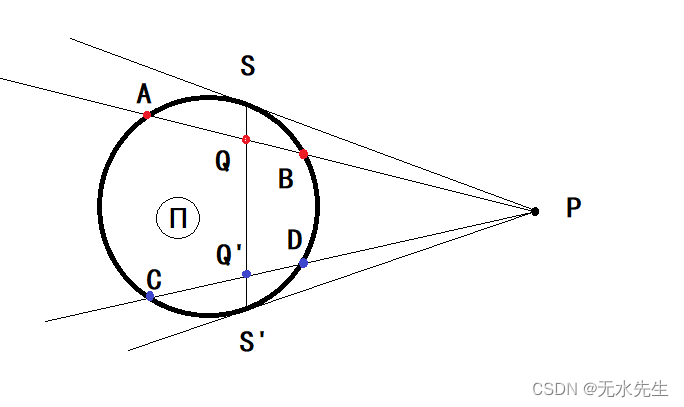
3.2 极点P在园内
如果P是极点,并且在单位圆内:不失一般性,将P放置在AB直径上,在P原地旋转后,滑动的时候
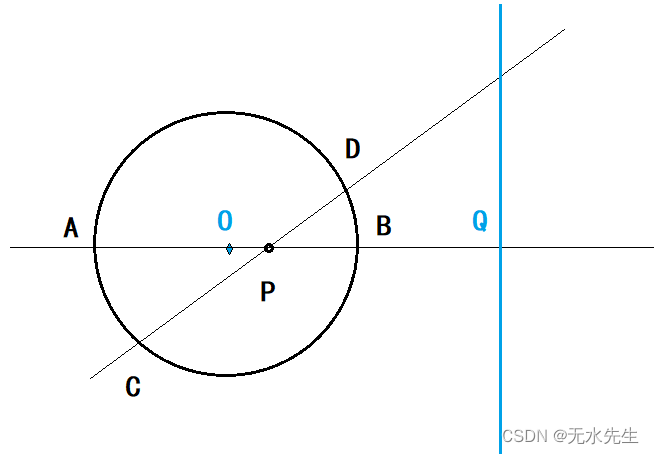
其中不变的性质是:AQ*BP=QB*AP;或CQ’*DP=Q'D*CP;通过这个性质,可以求出极线的位置:设 P( 0,s );BQ = x
AQ = 2 + x ; BQ = x ; BP = 1-s ; AP = 1+s
所以:(2+x)*(1-s)= x*(1+s)
最后得出:x = (1-s)/s
极线QQ‘坐标为:(1+x,t)或(1/s,t); t是参数;
四、椭圆的极点和极点
4.1 P是椭圆外的极点
设极点P在椭圆C外侧:P对应的极线方程与 椭圆C' 的两个交点实际上是从点P 向椭圆 C引出的两条切线的切点之连线。
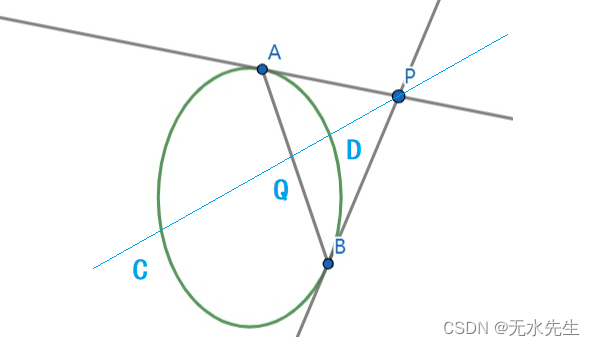
同样有性质:CQ *DP=QD*CP
4.2 极点在椭圆内部
性质1.内接四边形
设四边形ABCD内接于二次曲线C,则对角线交点P的极线是两组对边交点的连线。

在证明之前,我们先来证明一个引理.
引理:在完全四边形ABCDMN中,(C,E,A,M),(D,F,B,M)均为调和点列。(关于调和点列的定义,在上文极线的定义中有说明)

证明:对于 及塞瓦点P运用塞瓦定理有
对于 及截线MBD运用梅氏定理有:
联立以上两式知 即
∴ (C,E,A,M)为调和点列,类似可证明(D,F,B,M)为调和点列。
回到原命题
证明:由完全四边形的调和性质可知(C,E,A,M),(D,F,B,M)调和,
由极线的几何定义知点E在点M关于曲线C的极线上、点F在点M关于曲线C的极线上
由两点确定一条直线知,直线EF即为点M的极线,∴点P在点M的极线上
由配极原则知,点M在点P的极线上,同理可知,点N在点P的极线上
∴直线MN即为点P的极线,原命题成立。
五、双曲的极点和极线
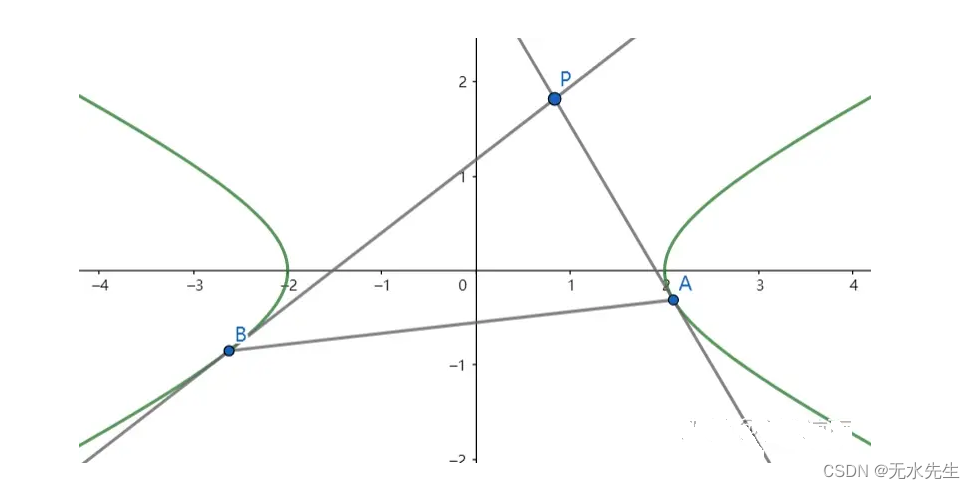
5.1 极点在双曲外侧
同样用【4.2 极点在椭圆内部】定理进行证明

5.2 极点在双曲内侧
则过极点 P 作双曲线 C的两条切线,切点正好为 A,B ,极线方程为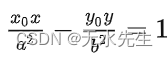 即为切点弦AB的直线方程。
即为切点弦AB的直线方程。
六、极点和极线性质
6.1 性质如下
Pole 和 polar 有几个有用的属性:
- 如果点极点 P 位于直线 l 上,则直线 l 的极点 L 位于点 P 的极线 p 上。
- 如果极点 P 沿直线 l 移动,则其极点 p 绕直线 l 的极点 L 旋转。
- 如果可以从极点到圆锥曲线绘制两条切线,则其极线通过两个切点。
- 如果一点位于圆锥截面上,则其极坐标是通过该点到圆锥截面的切线。
- 如果点 P 位于它自己的极线上,则 P 在圆锥曲线上。
- 相对于非退化圆锥截面,每条线恰好有一个极点。
- 任意两点 P 和 Q 到圆心的距离与彼此到另一极的距离成正比。
6.2 推论
性质1.配极原则推论
两点连线的极点是这两点的极线的交点;两直线交点的极线是这两直线的极点的连线。
证明:设有两点A、B,各自的极线交于C,则根据配极原则,C在A的极线上⇒A在C的极线上。同理,B在C的极线上。由两点确定一条直线可知AB是C的极线,即C是AB的极点。类似可证后者。
从这个性质中可以知道,对于二次曲线上两个点,过这两点的切线的交点的极线即这两点的连线。