推导

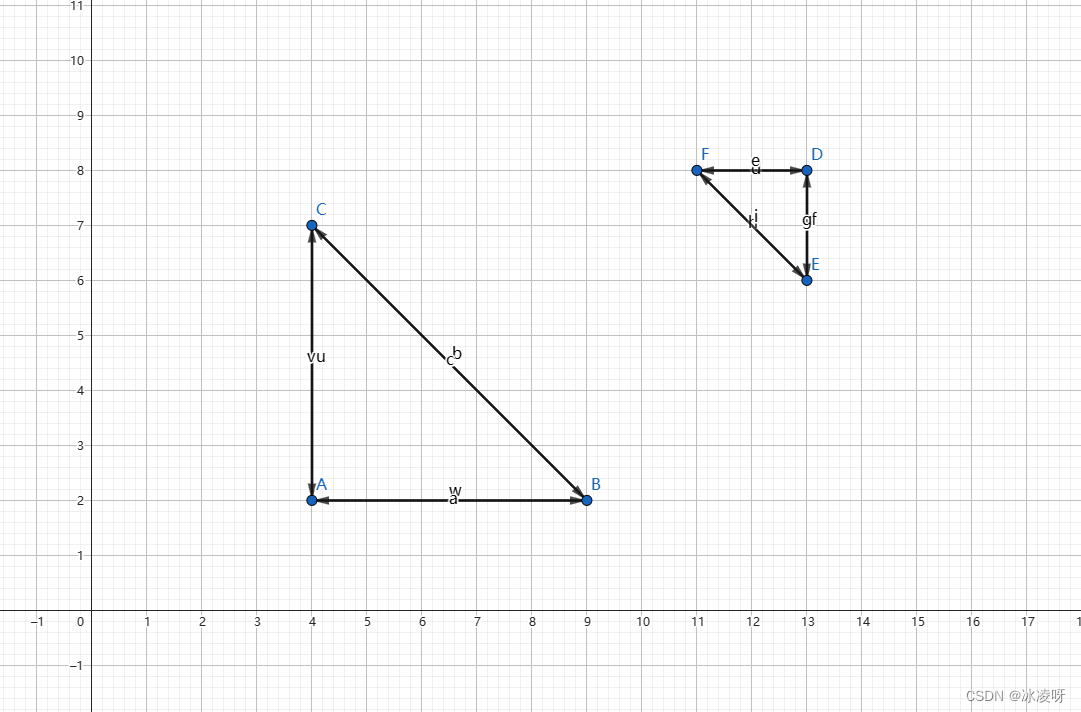
三角形ABC仿射成为三角形DEF的变换矩阵M

猜测矩阵M=

[

        [a1,b1,c1],

        [a2,b2,c2]

] 

仿射变换的数学联系

对于A点和D点

AX*a1+AY*b1+c1=DX

AX*a2+AY*b2+c1=DY

对于B点和E点

BX*a1+BY*b1+c1=EX

BX*a2+BY*b2+c2=EY

对于C点和F点

CX*a1+CY*b1+c1=FX

CX*a2+CY*b2+c2=FY

求解

对以上数学联系式均取第一条

AX*a1+AY*b1+c1=DX

BX*a1+BY*b1+c1=EX

CX*a1+CY*b1+c1=FX

可以看出这是一个三元一次方程组，我们可以借助scipy库linalg模块的solve函数进行求解，它的用法大家可以参考一下其他资料，这里不多赘述

对数学联系式均取第二条

AX*a2+AY*b2+c1=DY

BX*a2+BY*b2+c2=EY

CX*a2+CY*b2+c2=FY

也是一个三元一次方程组，同样可以借助scipy库linalg模块的solve函数进行求解

验证

根据以上各个点的坐标，分别用opencv的函数，和我们猜想的计算过程，观测对比两个结果是否一致

import numpy as np
import cv2 as cv
import math

AX = 4
AY = 2
BX = 9
BY = 2
CX = 4
CY = 7

DX = 13
DY = 8
EX = 13
EY = 6
FX = 11
FY = 8

ps1 = np.float32([
    [AX, AY],
    [BX, BY],
    [CX, CY]
])
ps2 = np.float32([
    [DX, DY],
    [EX, EY],
    [FX, FY]
])

M = cv.getAffineTransform(ps1, ps2)
print(f"opencv_M=\n{M}")

print()

A = np.array([
    [AX, AY, 1],
    [BX, BY, 1],
    [CX, CY, 1]
])
b1 = np.array([
    [DX],
    [EX],
    [FX]
])
b2 = np.array([
    [DY],
    [EY],
    [FY]
])
from scipy import linalg

r1 = linalg.solve(A, b1)
r2 = linalg.solve(A, b2)
r = np.array([
    r1.T[0],
    r2.T[0]
])
print(f"self_M=\n{r}")

运行结果

可以看出，结果是一致的，函数的底层实现原理就是如此