0. 前言

在做游戏的时候经常需要随机某一个点，而且形状各种各样，每次要随机的时候就容易忘记怎么弄了。这里总结一下各种常见形状内基础随机方式。

1. 矩形内随机

略~

/// <summary>
/// 在矩形区域内随机一个点
/// </summary>
public static Vector2 InRect(Rect rect)
{
    Vector2 pos = new Vector2();
    pos.x = Random.Range(0, rect.width) + rect.x;
    pos.y = Random.Range(0, rect.height) + rect.y;
    return pos;
}

2. 圆形内随机

圆形随机一般有两种。一种是通过极坐标来随机，另一种是先正常随机矩形在判断点是否在圆形内。第二种其实使用的范围很广，我们后面在 “ 6.拒绝采样随机 ” 单独讲，这里我们先讲第一种。

圆形通过极坐标随机就比较简单，分别随机半径和角度。不过直接随机的情况下，概率是不均匀的。也比较容易理解，比如随机到半径为1和为2的圆大小是不一样大的，但是其享受的概率是一样的，所以呢，会出现圆中心概率更高的情况。这个时候只要在[0,r*r]的范围内进行随机再sqrt开方就可以了，就可以弥补这个概率，具体推导可以用换元法试试。这里放一下代码

public struct Circle
{
    public Vector2 center;
    public float radius;

    public Circle(Vector2 center, float radius)
    {
        this.center = center;
        this.radius = radius;
    }
}
/// <summary>
/// 在圆形区域内随机一个点
/// </summary>
public static Vector2 InCircle(Circle circle)
{
    //  通过极坐标来随机
    float r = Mathf.Sqrt(Random.Range(0, circle.radius));
    float angle = Random.Range(0, Mathf.PI * 2);
    Vector2 pos = new Vector2(Mathf.Cos(angle) * r, Mathf.Sin(angle) * r);
    pos += circle.center;
    return pos;
}

至于从直角坐标的角度，先随机x，然后获取y的范围进行随机也会有概率不均匀的问题，具体处理还得重新推导，这里就不再研究了。

3. 三角形内随机

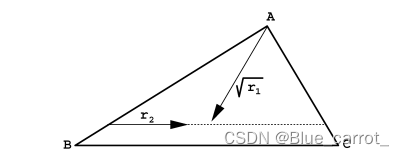
三角形随机意外要麻烦得多。简单讲一种思路。我们可以先随机三角形的一条边上的高，随机这个高度并再这个高度的情况下，去随机平行边的长度。

比如下图，我们先随机h再随机r的情况来得到点p。

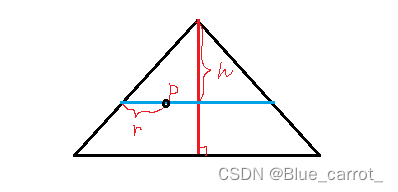
那么在这种情况下也是会有概论不均衡的问题的，不过这里我们可以发现，因为做的是平行线的缘故，h和得到的平行线是等比放大和缩小的，所以可以用类似于圆的方式来随机。不过实现起来好麻烦呀，太难了，对于已经毕业的人来说，数学太难了。

这里我找到的了一种类似的方法，非常简单，具体论证如果有想了解的话，大家看一下后面链接吧。

那么实现代码就是这样的。

public struct Triangle
{
    public Vector2 a;
    public Vector2 b;
    public Vector2 c;

    public Triangle(Vector2 a, Vector2 b, Vector2 c)
    {
        this.a = a;
        this.b = b;
        this.c = c;
    }
}
/// <summary>
/// 在三角形区域内随机一个点
/// </summary>
public static Vector2 InTriangle(Triangle triangle)
{
    // Vector2 a, Vector2 b, Vector2 c
    Vector2 pos = new Vector2();
    float r1 = Random.Range(0f, 1f);
    float r2 = Random.Range(0f, 1f);
    pos = (1 - Mathf.Sqrt(r1)) * triangle.a +
        Mathf.Sqrt(r1) * (1 - r2) * triangle.b +
        Mathf.Sqrt(r1) * r2 * triangle.c;
    return pos;
}

4. 多边形内随机

多边形随机可以先把多边形分解为三角形，然后再根据三角形的面积分配不同的权重，随机一个三角形，然后在该三角形内进行随机。所以这个问题，又可以分解为以下几个点。

• 多边形分隔为三角形
• 三角形面积计算
• 按权重随机
• 三角形内随机一点

这样的方法其实流程颇为麻烦， 另一种方法是，像刚刚提及的一样，先矩形简单随机再判断是否在多边形内来达到随机目的，这个还是在 “6.拒绝采样随机” ，进行详细介绍。

那接下来就依次处理一下刚刚的问题。

（1）多边形分割为三角形

关于第一点其实还挺麻烦的，具体怎么分割为三角形有挺多不同的方法，耳切法是一种目前我能查到的一种常见方法，具体内容之前也有讲过，链接如下，实在太长这里就不展开解释了。

https://blog.csdn.net/Blue_carrot_/article/details/131192660

（2）三角形面积计算

这里用的是公式直接去计算就可以了，S=√[p(p-l1)(p-l2)(p-l3)]（p为半周长），又解决咯。

/// <summary>
/// 获取三角形面积
/// </summary>
/// <returns></returns>
public float Area()
{
    //  S=√[p(p-l1)(p-l2)(p-l3)]（p为半周长）
    float l1 = (b - a).magnitude;
    float l2 = (c - b).magnitude;
    float l3 = (a - c).magnitude;
    float p = (l1 + l2 + l3) * 0.5f;
    return Mathf.Sqrt(p * (p - l1) * (p - l2) * (p - l3));
}

（3）数据缓存

其实到这里我们可以发现，这种情况下要随机一个多边形的操作还是非常麻烦的。但是包括划分为三角形，计算三角形面积，这些其实都是可以把数据缓存下来的，这样下次还是可以接着用，就会快非常多。那么我们可以定义数据结构如下。

public struct PolygonRandomData
{
    public Polygon polygon;
    public Triangle[] triangles;
    public float polygonArea;
    public float[] trianglesArea;

    public PolygonRandomData(Polygon polygon)
    {
        // 三角化
        this.polygon = polygon;
        triangles = polygon.Triangulate();

        // 计算面积
        float area;
        trianglesArea = new float[triangles.Length];
        polygonArea = 0;
        for (int i = 0; i < triangles.Length; i++)
        {
            area = triangles[i].Area();
            polygonArea += area;
            trianglesArea[i] = area;
        }
    }
}

如果需要重复随机的话就可以先把这些数据缓存一下，降低开销。

（4）按权重随机

权重随机，目前做法就是先从0到权重和随机一个数，然后遍历叠加，去判断到达了没，以此达到目的。代码如下，权重和这里是由外部提供 ，因为我们刚刚其实也以及已经把面积和计算好了，就不用再计算一次。

/// <summary>
/// 按照数组内数的非负数权重，获取随机的索引。
/// 如果数组为空或者长度为0，将返回-1。
/// </summary>
/// <param name="weightArr">权重数组，应为非负数</param>
/// <param name="weightSum">给定的权重和，应为weightArr的权重之和</param>
/// <returns></returns>
public static int IndexInWeightArr(float[] weightArr, float weightSum)
{
    int index = -1;
    float cur = Random.Range(0, Mathf.Max(0, weightSum));
    float sum = 0;
    if (weightArr != null && weightArr.Length > 0)
    {
        index = 0;
        for (; index < weightArr.Length; index++)
        {
            sum += weightArr[index];
            if (sum > cur)
            {
                break;
            }
        }
        if (index >= weightArr.Length)
        {
            index = weightArr.Length - 1;
        }
    }
    return index;
}

下面是只提供权重数组的方法。

/// <summary>
/// 按照数组内数的非负数权重，获取随机的索引。
/// 如果数组为空或者长度为0，将返回-1。
/// </summary>
/// <param name="weightArr">权重数组，应为非负数</param>
/// <returns></returns>
public static int IndexInWeightArr(float[] weightArr)
{
    float weightSum = ArrayMathF.Sum(weightArr);
    return IndexInWeightArr(weightArr, weightSum);
}

public static float Sum<T>(T arr) where T : IEnumerable<float>
{
    float sum = 0;
    if (arr != null)
    {
        foreach (var value in arr)
        {
            sum += value;
        }
    }
    return sum;
}

（5）实现随机

至于三角形内随机，我们在前面已经解决了，此时就可以实现这个多边形随机了，如下！

 /// <summary>
/// 在多边形区域内内随机一个点
/// </summary>
public static Vector2 InPolygon(Polygon polygon, Vector2 defaultValue)
{
    return InPolygon(new PolygonRandomData(polygon), defaultValue);
}

/// <summary>
/// 在多边形区域内内随机一个点，polygonData为多边形三角化相关数据
/// </summary>
public static Vector2 InPolygon(PolygonRandomData polygonData, Vector2 defaultValue)
{
    Vector2 pos = defaultValue;
    int index = IndexInWeightArr(polygonData.trianglesArea, polygonData.polygonArea);
    if (index != -1)
    {
        pos = InTriangle(polygonData.triangles[index]);
    }
    return pos;
}

这里用了defaultValue主要是考虑到，多边形可能为非简单多边形，比如边有交叉或者点少于3个这种情况，会有分割三角形失败的问题，所以使用了这个值来可以提供后续识别或者保护处理。

5. 随机点测试

前面也列举的了挺多情况，这里先简单测试一下随机效果。每个图形绘制为红色，其中每个图形随机500点，画为绿色，测试结果如下。

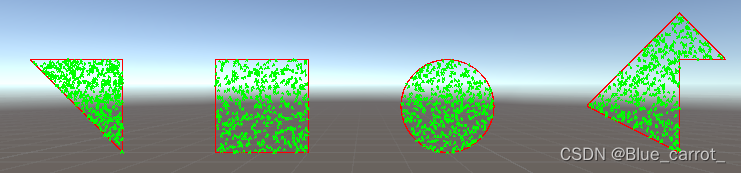
可以看出也是随机点的分布还是比较均匀的，效果还可以。

6. 拒绝采样随机

终于到了这个环节。通常我们会有很多奇奇怪怪的形状，没办法具体来形容或者很难去推断去随机方法，甚至还有新的还有额外的条件。那么这个时候我们就可以用到拒绝采样的这样一种方式了。这种方式就是为了从一个简单的概率分布得到一个复杂的概率分布。

比如，我们想要随机一个圆内的点，我们先在矩形内随机，然后判断是否在圆形内，如果不在就拒绝，然后重新随机一下。这样我们就可以得到一个分布均匀的圆啦。这个过程就是拒绝采样了，那么程序上实现的话可以如下：

/// <summary>
/// 拒绝采样，在矩形区域内随机一个符合条件的点
/// </summary>
/// <param name="rect"></param>
/// <param name="judgeFunc"></param>
/// <returns></returns>
public static Vector2 RejectSampling(Rect rect, System.Func<Vector2, bool> judgeFunc)
{
    return RejectSampling(rect, judgeFunc, Vector2.zero, -1);
}

/// <summary>
/// 拒绝采样，在矩形区域内随机一个点，并判断是否符合条件，不符合再次随机
/// </summary>
/// <param name="rect">范围</param>
/// <param name="judgeFunc">判断条件</param>
/// <param name="defaultValue">失败返回坐标</param>
/// <param name="maxRandomTime">最大尝试次数,当 maxRandomTime <= 0 时，将无限尝试直到要求被满足</param>
/// <returns></returns>        
public static Vector2 RejectSampling(Rect rect, System.Func<Vector2, bool> judgeFunc, Vector2 defaultValue, int maxRandomTime)
{
    Vector2 pos;
    for (; maxRandomTime != 0; maxRandomTime--)
    {
        pos = InRect(rect);
        if (judgeFunc(pos))
        {
            return pos;
        }
    }
    return defaultValue;
}

这里会发现我其实给了额外的停止条件，因为在程序中不断循环是有风险的，如果万一这个条件是不可能在范围内达到的，到时候就直接死循环了，所以给定一个范围来提供保护还是挺有用的。

至于判断条件用的是委托的方式，注意了委托在创建的时候会有额外的开销，但正常传值调用的开销是和正常函数差不多的。所以不用过于担心，如果要多次随机，可以把委托先保存一下。

7. 拒绝采样样例

这里测试一下拒绝采样的效果，其实做拒绝采样随机的步骤就可以变化为两步

• 确定随机范围，获取外包裹矩形
• 确定随机条件，判断点是否在形状内

下面我们用两个比较麻烦的图形，椭圆和多边形来做这个拒绝采样处理试试。

（1）椭圆内随机

椭圆内随机一点，变成椭圆外包裹矩形和判断是否在椭圆内，这个都比较简单，就直接代码咯

public struct Ellipse
{
    public Vector2 center;
    public float a;
    public float b;

    public Ellipse(Vector2 center, float a, float b)
    {
        this.center = center;
        this.a = a;
        this.b = b;
    }

    public Rect OutsideRect()
    {
        Vector2 size = new Vector2(a, b);
        return new Rect(center - size, size * 2);
    }

    public bool Inside(Vector2 pos)
    {
        pos -= center;
        return pos.x * pos.x / (a * a) + pos.y * pos.y / (b * b) < 1;
    }
}

那么获得者两个条件后，就可以开始随机了，如下就可以得到椭圆的点了

System.Func<Vector2, bool> judgeFunc = ellipse.Inside;
Rect ellipseOutsideRect = ellipse.OutsideRect();
Vector2 pos = RandomU.RejectSampling(ellipseOutsideRect, judgeFunc, Vector2.zero, 100);

（2）多边形内随机

判断多边形的外包裹矩形，就可以直接遍历所有点，找出xmin，xmax，ymin，ymax就可以得到这个矩形了，代码如下

public Rect OutsideRect()
{
    if (points.Length <= 0)
    {
        return new Rect(0, 0, 0, 0);
    }
    Vector2 min = points[0];
    Vector2 max = points[0];
    for (int i = 0; i < points.Length; i++)
    {
        max.x = Mathf.Max(points[i].x, max.x);
        max.y = Mathf.Max(points[i].y, max.y);
        min.x = Mathf.Min(points[i].x, min.x);
        min.y = Mathf.Min(points[i].y, min.y);
    }
    return new Rect(min, max - min);
}

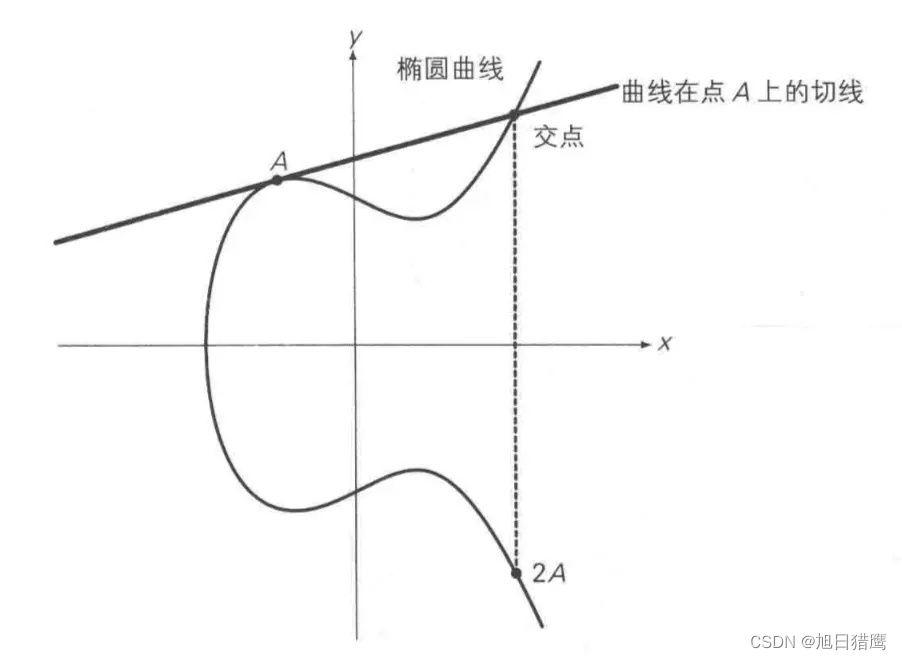
判断点是否在多边形内部（点如果在多边形边上，也不属于内部），方法就有很多了，这里用的是做射线判断交点的方法，可以看下图。

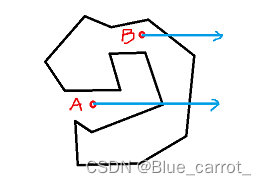
A点在多边形外做射线的交点都会是偶数个，而B点在多边形内做射线交点为奇数个，就可以作为我们判断的依据。而且一般会用水平右方向的射线，比较容易理解和计算。需要考虑特殊情况就是如果多边形的点在射线上的情况，可不可以判断为相交？如下图。

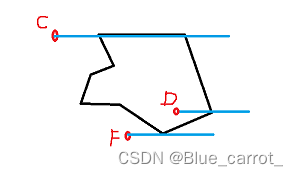
这里的CDF点都会有不同情况的交点表现，这里就可以做其他限制。

• 对于边的线段有端点在射线上的情况（如F，D），只考虑下端点（记为N），忽视上端点（记为M）。就是N在射线上，交点数量+1，M在不在射线上都不考虑为交点。（这里上下端点相反过来也是一样效果）。
• 对于边的射线都在端点上的情况，视为无交点。

在加上这个两个处理后，再去数交点的数量，是不是就可以满足之前提出的交点数奇偶判断在不在多边形内？大家可以试一下。那么代码就如下了。

/// <summary>
/// 点是否在多边形（在边上视为在多边外）
/// </summary>
/// <param name="pos"></param>
/// <returns></returns>
public bool Inside(Vector2 pos)
{
    int j = points.Length - 1;
    bool inside = false;
    Vector2 pi, pj;
    for (int i = 0; i < points.Length; i++)
    {
        pi = points[i];
        pj = points[j];
        j = i;
        // 水平右方向射线，看交点个数
        if ((
            // 点的y值是否在两点之间，区间只选一边，
            // 这样每个就只会算一次，避免当有点在射线上的干扰
            (pi.y <= pos.y && pos.y < pj.y) || (pj.y <= pos.y && pos.y < pi.y)) &&
            // x轴截距
            pos.x < (pj.x - pi.x) * (pos.y - pi.y) / (pj.y - pi.y) + pi.x)
        {
            inside = !inside;
        }
    }
    return inside;
}

（3）效果

对于上述的两个形状来试试效果，还挺均匀的。效率问题其实也还好，因为其实随机到图形内的这个情况还是概率比较高的，重复几次基本就随机到了。

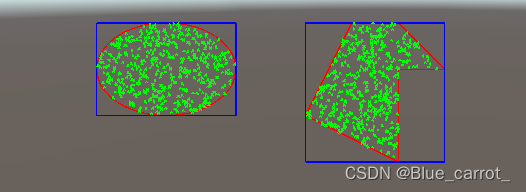
（4）点是否三角形/圆形内

其他图形用这个方法也是大同小异，这里就再简单列举一下其他图形如何判断点是否在形状内。
三角形：

/// <summary>
/// 是否在三角形内
/// </summary>
/// <returns></returns>
public bool Inside(Vector2 pos)
{
    Vector3 pa = a - pos;
    Vector3 pb = b - pos;
    Vector3 pc = c - pos;
    Vector3 pab = Vector3.Cross(pa, pb);
    Vector3 pbc = Vector3.Cross(pb, pc);
    Vector3 pca = Vector3.Cross(pc, pa);
    float d1 = Vector3.Dot(pab, pbc);
    float d2 = Vector3.Dot(pab, pca);
    float d3 = Vector3.Dot(pbc, pca);
    return d1 > 0 && d2 > 0 && d3 > 0;
}

圆形：

/// <summary>
/// 是否在圆形内
/// </summary>
/// <returns></returns>
public bool Inside(Vector2 pos)
{
    pos -= center;
    return pos.x * pos.x + pos.y * pos.y < radius * radius;
}

8. 结束咯

到这里就结束咯，希望能够对游戏中进行随机处理，起到参考作用~

相关参考文章
三角形内随机处理
http://www.cs.princeton.edu/~funk/tog02.pdf
https://www.jianshu.com/p/36fa431311ac
不规则、三角形面积计算
https://blog.csdn.net/n_moling/article/details/115381804
Unity3d判断一个点是否在多边形内
https://blog.csdn.net/zouxin_88/article/details/109678109