• https://leetcode.cn/problems/perfect-squares/

题目描述

• 给你一个整数 n ，返回 和为 n 的完全平方数的最少数量。
  完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4
示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

class Solution {
public:
    int numSquares(int n) {

    }
};

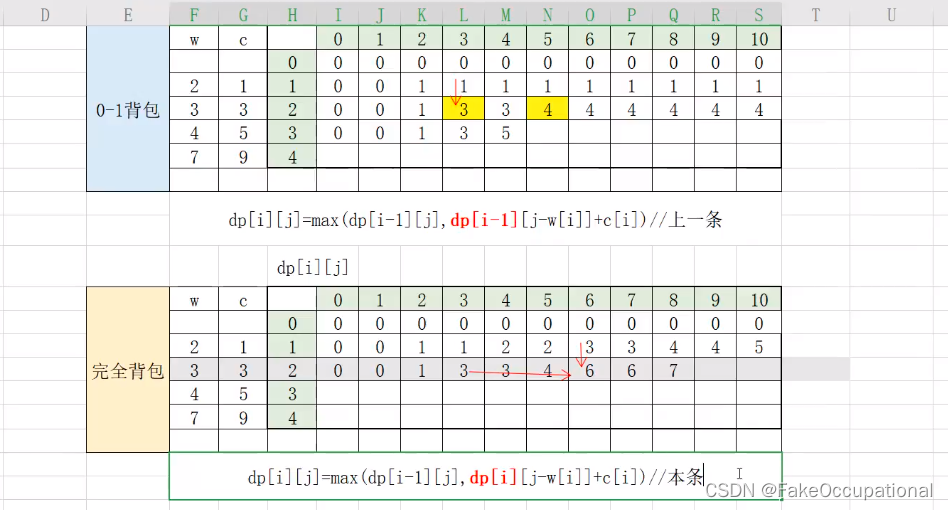
完全背包

• 恰好装满之类的01背包问题，竖向i是物品，横向j是容量。 i为前i件物品,容量j可以为0，算法主题为遍历i,j 。
  由于无后效性，只知道nums[i],需要判断j-nums[i]能做什么。
  j-nums[i]为装了当前物品剩余的空间。dp[ i-1][j-nums[i]]为这点空间能做的事情。如果最大化利润则为以下公式：
  $dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v_i)$

• 完全背包每次还是考虑当前项，只不过可以拿多个,那我们可以加个循环k
  $dp[i][j]=max(dp[i-1][j],dp[i-1][j-w_i\ast k]+v_i)$

• 实际上j是从小到大遍历的，所以可以用
  $dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v_i)$
  省略掉一个循环

• 0-1背包如果压缩维度dp[i][j-nums[i]]，但是j需要倒序遍历。

完全背包

        完全背包是一类经典的背包问题，与0/1背包问题和多重背包问题不同。其中，每个物品可以被无限次地选择放入背包。也就是说，每个物品的数量是无限的。

        假设有一个容量为$V$的背包，现在有$n$个物品，每个物品的体积为$w_i$，价值为$v_i$，同时每个物品的数量是无限的。问能够放入背包的最大价值是多少？

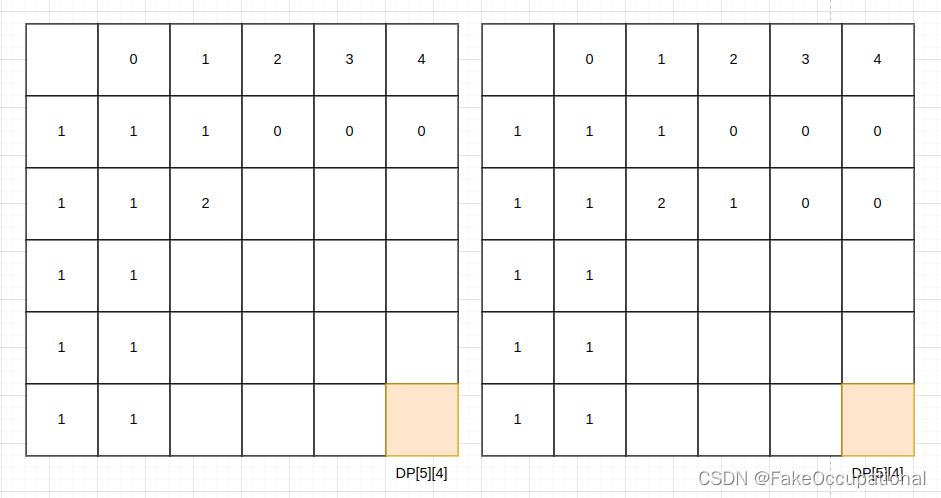
        完全背包问题可以通过动态规划求解，时间复杂度为$O(nV)$。可以用一个二维数组$dp[i][j]$来表示前$i$个物品放入容量为$j$的背包中获得的最大价值。其中，状态转移方程为$dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v_i)$，表示当前物品不放入背包或者放入背包均可。

• （二维的转移方程还是比较好记的，只需要将$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w_i]+v_i)$写成i就行）

$$\sqrt{13}=\sqrt{9}=3$$

	0	1	2	3	4	5	6	7	8	9	10	11	12	13
1
2
3

$$"能够放入背包的最大价值"\Rightarrow "能够放入背包的最小价值"(每个数的价值为1)$$
$$dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v_i)$$

$$dp[i][j]=min(dp[i-1][j],dp[i][j-w_i]+1)$$

class Solution {
public:
    // 求平方后小于 n 的最大完全平方数
    int min_sq(int n) {
        int ans = 1;
        for ( int i=1;i<n;i++ ) {
            if ( i*i>n )
                break;
            ans = i;
        }
        return ans;
    }

    int numSquares(int n) {

        // // 记忆化搜索
        // int m = min_sq(n), cache[m+1][n+1];
        // memset(cache, -1, sizeof(cache));
        // function<int(int,int)> dfs = [&](int i, int c) -> int {
        //     if ( i<0 )
        //         return c==0 ? 0 : INT_MAX/2;
        //     if ( cache[i][c]!=-1 )
        //         return cache[i][c];
        //     if ( c<(i+1)*(i+1) )
        //         return cache[i][c] = dfs(i-1, c);
        //     return cache[i][c] = min(dfs(i-1, c), dfs(i, c-(i+1)*(i+1))+1);
        // };

        // return dfs(m-1, n);

        // // 1:1 递推
        // int m = min_sq(n), f[m+1][n+1];
        // memset(f, 0x3f, sizeof(f));
        // f[0][0] = 0;
        // for ( int i=0;i<m;++i ) {
        //     for ( int c=0;c<n+1;++c ) {
        //         if ( c<(i+1)*(i+1) )
        //             f[i+1][c] = f[i][c];
        //         else
        //             f[i+1][c] = min(f[i][c], f[i+1][c-(i+1)*(i+1)]+1);
        //     }
        // }
        // return f[m][n];

        // // 滚动双数组空间优化
        // int m = min_sq(n), f[2][n+1];
        // memset(f, 0x3f, sizeof(f));
        // f[0][0] = 0;
        // for ( int i=0;i<m;++i ) {
        //     for ( int c=0;c<n+1;++c ) {
        //         if ( c<(i+1)*(i+1) )
        //             f[(i+1)%2][c] = f[i%2][c];
        //         else
        //             f[(i+1)%2][c] = min(f[i%2][c], f[(i+1)%2][c-(i+1)*(i+1)]+1);
        //     }
        // }
        // return f[m%2][n];

        // 单数组空间优化
        int m = min_sq(n), f[n+1];
        memset(f, 0x3f, sizeof(f));
        f[0] = 0;
        for ( int i=0;i<m;++i ) {
            for ( int c=0;c<n+1;++c ) {
                if ( c>=(i+1)*(i+1) )
                    f[c] = min(f[c], f[c-(i+1)*(i+1)]+1);
            }
        }
        return f[n];
    }
};

// 作者：thirikid
// 链接：https://leetcode.cn/problems/perfect-squares/solution/ling-shen-wan-quan-bei-bao-hui-su-ji-yi-d48mb/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

一维

这个问题可以通过动态规划求解。我们可以用一个一维数组 $dp$ 来表示和为 $i$ 的完全平方数的最少数量，状态转移方程为：

d p [ i ] = min ⁡ j = 1 i { d p [ i − j 2 ] + 1 } dp[i] = \min_{j=1}^{\sqrt{i}} \{dp[i-j^2] + 1\} dp[i]=j=1mini ​​{dp[i−j2]+1}

其中，$j$ 表示一个完全平方数，$i-j^2$ 表示剩余的部分。也就是说，要计算和为 $i$ 的完全平方数的最少数量，我们需要枚举最后一个完全平方数 $j$，并计算剩余部分 $i-j^2$ 的最少数量，最后加上 1 即可。

初始状态为 $dp[0]=0$，因为和为 $0$ 的完全平方数数量为 $0$。

最终的答案为 $dp[n]$。以下是Python代码实现：

def numSquares(n: int) -> int:
    # 初始化状态
    dp = [float('inf')] * (n + 1)
    dp[0] = 0

    # 状态转移
    for i in range(1, n+1):
        for j in range(1, int(i ** 0.5) + 1):
            dp[i] = min(dp[i], dp[i - j*j] + 1)

    return dp[n]