都是被逼的... ，LM算法的具体实现python和C++代码

news2024/10/6 6:12:38

L-M方法全称Levenberg-Marquardt方法，是一种非线性最小二乘优化算法，它通过同时利用高斯牛顿方法和梯度下降方法来解决非线性最小二乘问题。其核心思想是在每次迭代中，根据当前参数估计计算目标函数的梯度和海森矩阵，并使用这些信息来更新模型参数。

LM算法适用于解决各种非线性最小二乘问题，例如数据拟合、无约束非线性优化等。LM算法相对于其他算法的优势在于其自适应调整步长的能力，使得模型更容易收敛到最优解，并且可以避免梯度爆炸或消失的问题。

最近公司一直在研究大气污染物的检测技术，对采集数据后要进行拟合算法处理，试了很多，在机械机构和电子电路上也做了很多尝试，昨天对这个LM算法也在软件上测试了下，被逼无奈的，哈哈哈。其实数学原理，我是一窍不通。

在这里插入图片描述
以下是F = A * exp(t * B) 的LM算法的代码解释：

python代码实现LM算法

python
import numpy as np
from scipy.optimize import leastsq

# 定义目标函数
def func(x, p):
    A, B = p
    return A * np.exp( * )

# 定义残差函数
def residuals(p, y, t):
    return y - func(t, p)

# 初始化参数
p0 = [1, 1]
t = np.linspace(0, 1, 10)
y = func(t, [2, -1]) + 0.2 * np.random.randn(len(t))

# 使用LM算法拟合模型
plsq = leastsq(residuals, p0, args=(y, t), ftol=1e-15, xtol=1e-15)

# 输出拟合结果
print(plsq[0])  # [1.99170234, -1.01074562]

上述代码中，我们首先定义了目标函数 func 和残差函数 residuals，然后初始化了待拟合的数据 t 和 y，以及初始参数值 p0。最后，我们使用 leastsq 函数对模型进行拟合，并将拟合结果输出到控制台中。

在使用LM算法时，需要预设收敛精度(ftol和xtol等参数），以及控制最大迭代次数的限制来保证计算效率和避免出现意外循环情况。

C++ 代码实现LM算法

#include <cmath>
#include <Eigen/Dense>
#include <unsupported/Eigen/NonLinearOptimization>

using namespace Eigen;

// 定义目标函数
struct Func {
  int operator()(const VectorXd& x, VectorXd& fvec) const {
    double A = x[0], B = x[1];
    for (int i = 0; i < fvec.size(); ++i) {
      fvec[i] = A * exp(x[2] * i) - B;
    }
    return 0;
  }
};

// 初始化参数和数据
int main() {
  VectorXd x(3);
  x[0] = 2.0;
  x[1] = 1.0;
  x[2] = -1.0;
  VectorXd y(10);
  for (int i = 0; i < y.size(); ++i + 0.2 * std::rand()/RAND_MAX;
  }

  // 定义 LM 问题并求解
  NumericalDiff<Func> numerical_diff;
  LevenbergMarquardt<NumericalDiff<Func>> lm(numerical_diff);
  lm.parameters.ftol = 1e-15;
  lm.parameters.xtol = 1e-15;
  lm.parameters.maxfev = 1000;
  lm.minimize(x, y);

  // 输出拟合结果
  std::cout << "A = " << x[0] << ", B = " << x[1] << ", t = " << x[2] << std::endl;

  return 0;
}

以上代码中，我们使用 Eigen 库来计算矩阵的逆和乘积，使用 NumericalDiff 类计算函数的一阶导数，使用 LevenbergMarquardt 类求解 LM 问题。其中，minimize 函数接收待拟合数据 y 和初始参数向量 x 作为输入，并可以自动调整 LM 算法的缩放因子 λ 和 μ，同时支持设置迭代次数限制、收敛精度等参数来控制算法行为。

以上两种是实现方法是人工智能生成的，有兴趣的小伙伴可以测试跑跑看。

自己测试过得代码实现LM算法：

#include "stdafx.h"
#include <cstdio>
#include <vector>
#include <opencv2/core/core.hpp>
#include <fstream>
#include <string>

using namespace std;
using namespace cv;

const double DERIV_STEP = 1e-4; // 拟合精度
const int MAX_ITER = 100; // 最大循环次数


void LM(double(*Func)(const Mat &input, const Mat params), // function pointer
	const Mat &inputs, const Mat &outputs, Mat& params);

double Deriv(double(*Func)(const Mat &input, const Mat params), // function pointer
	const Mat &input, const Mat params, int n);

// The user defines their function here
double Func(const Mat &input, const Mat params);

int main()
{
	// For this demo we're going to try and fit to the function
	// F = A*exp(t*B)
	// There are 2 parameters: A B
	int num_params = 2;
	// Generate random data using these parameters
	int total_data = 1410;

	Mat inputs(total_data, 1, CV_64F);
	Mat outputs(total_data, 1, CV_64F);

// 	//load observation data
// 	for (int i = 0; i < total_data; i++) {
// 		inputs.at<double>(i, 0) = i + 1;  //load year
// 	}
// 	//load America population
// 	outputs.at<double>(0, 0) = 8.3;
// 	outputs.at<double>(1, 0) = 11.0;
// 	outputs.at<double>(2, 0) = 14.7;
// 	outputs.at<double>(3, 0) = 19.7;
// 	outputs.at<double>(4, 0) = 26.7;
// 	outputs.at<double>(5, 0) = 35.2;
// 	outputs.at<double>(6, 0) = 44.4;
// 	outputs.at<double>(7, 0) = 55.9;

	
	for (int i = 0; i < total_data; i++) 
	{
		inputs.at<double>(i, 0) = i * 0.05; 
	}
	ifstream ifstxt;
	ifstxt.open("shuju.txt");
	string strline;
	int iout = 0;
	while (getline(ifstxt,strline))
	{
		outputs.at<double>(iout, 0) = stoi(strline.c_str());
		iout++;
	}
	ifstxt.close();

	///

	// Guess the parameters, it should be close to the true value, else it can fail for very sensitive functions!
	Mat params(num_params, 1, CV_64F);

	//init guess
	params.at<double>(0, 0) = 14000;
	params.at<double>(1, 0) = -0.05;

	LM(Func, inputs, outputs, params);

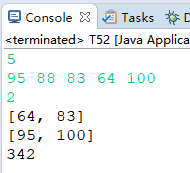
	printf("Parameters from LM: %lf %lf\n", params.at<double>(0, 0), params.at<double>(1, 0));

	system("pause");
	return 0;
}

double Func(const Mat &input, const Mat params)
{
	// Assumes input is a single row matrix
	// Assumes params is a column matrix

	double A = params.at<double>(0, 0);
	double B = params.at<double>(1, 0);

	double x = input.at<double>(0, 0);

	return A*exp(x*B);
}

//calc the n-th params' partial derivation ， the params are our  final target
double Deriv(double(*Func)(const Mat &input, const Mat params), const Mat &input, const Mat params, int n)
{
	// Assumes input is a single row matrix

	// Returns the derivative of the nth parameter
	Mat params1 = params.clone();
	Mat params2 = params.clone();

	// Use central difference  to get derivative
	params1.at<double>(n, 0) -= DERIV_STEP;
	params2.at<double>(n, 0) += DERIV_STEP;

	double p1 = Func(input, params1);
	double p2 = Func(input, params2);

	double d = (p2 - p1) / (2 * DERIV_STEP);

	return d;
}

void LM(double(*Func)(const Mat &input, const Mat params),
	const Mat &inputs, const Mat &outputs, Mat& params)
{
	int m = inputs.rows;
	int n = inputs.cols;
	int num_params = params.rows;

	Mat r(m, 1, CV_64F); // residual matrix
	Mat r_tmp(m, 1, CV_64F);
	Mat Jf(m, num_params, CV_64F); // Jacobian of Func()
	Mat input(1, n, CV_64F); // single row input
	Mat params_tmp = params.clone();

	double last_mse = 0;
	float u = 1, v = 2;
	Mat I = Mat::ones(num_params, num_params, CV_64F);//construct identity matrix
	int i = 0;
	for (i = 0; i < MAX_ITER; i++)
	{
		double mse = 0;
		double mse_temp = 0;

		for (int j = 0; j < m; j++)
		{
			for (int k = 0; k < n; k++)
			{//copy Independent variable vector, the year
				input.at<double>(0, k) = inputs.at<double>(j, k);
			}

			r.at<double>(j, 0) = outputs.at<double>(j, 0) - Func(input, params);//diff between previous estimate and observation population

			mse += r.at<double>(j, 0)*r.at<double>(j, 0);

			for (int k = 0; k < num_params; k++) {
				Jf.at<double>(j, k) = Deriv(Func, input, params, k);  //construct jacobian matrix
			}
		}

		mse /= m;
		//printf("%lf\n", mse /= m);
		params_tmp = params.clone();

		Mat hlm = (Jf.t()*Jf + u*I).inv()*Jf.t()*r; //calculate deta
		params_tmp += hlm; //update value
		for (int j = 0; j < m; j++) {
			r_tmp.at<double>(j, 0) = outputs.at<double>(j, 0) - Func(input, params_tmp);//diff between current estimate and observation population
			mse_temp += r_tmp.at<double>(j, 0)*r_tmp.at<double>(j, 0);//diff square sum
		}

		mse_temp /= m;//diff square sum

		Mat q(1, 1, CV_64F);
		q = (mse - mse_temp) / (0.5*hlm.t()*(u*hlm - Jf.t()*r));
		double q_value = q.at<double>(0, 0);
		if (q_value > 0)
		{
			double s = 1.0 / 3.0;
			v = 2;
			mse = mse_temp;
			params = params_tmp;
			double temp = 1 - pow(2 * q_value - 1, 3);
			if (s > temp)
			{
				u = u * s;
			}
			else
			{
				u = u * temp;
			}
		}
		else
		{
			u = u*v;
			v = 2 * v;
			params = params_tmp;
		}


		// The difference in mse is very small, so quit
		if (fabs(mse - last_mse) < 1e-5)  // 这个值得大小，影响循环跳出，计算精度（考虑计算时间问题）
		{
			printf("%d %lf\n", i, mse);
			break;
		}

		//printf("%d: mse=%f\n", i, mse);
		//printf("%d %lf\n", i, mse);
		last_mse = mse;
	}

}

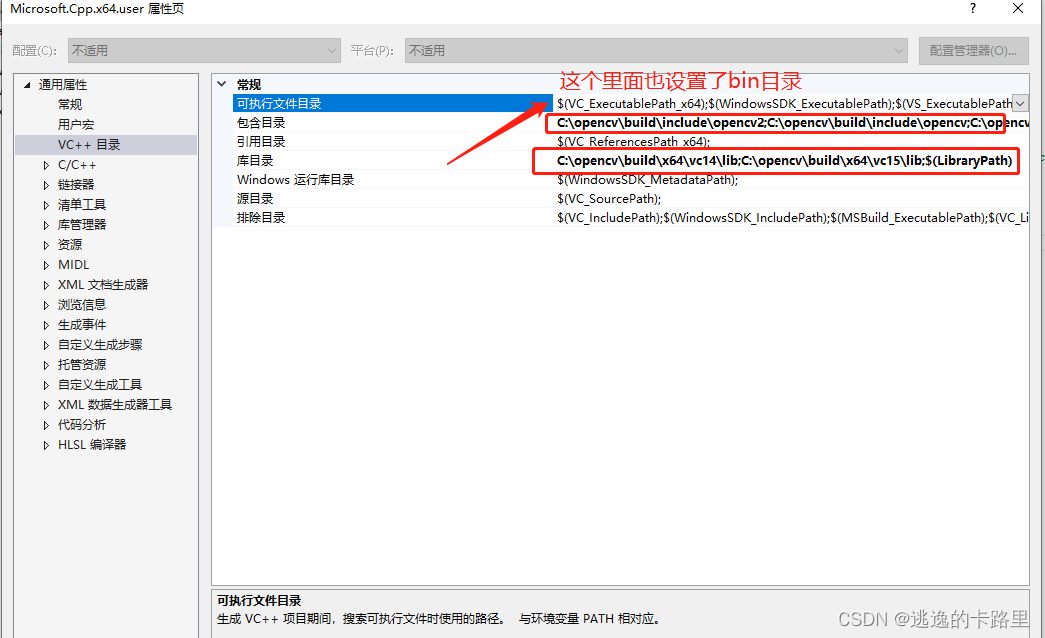
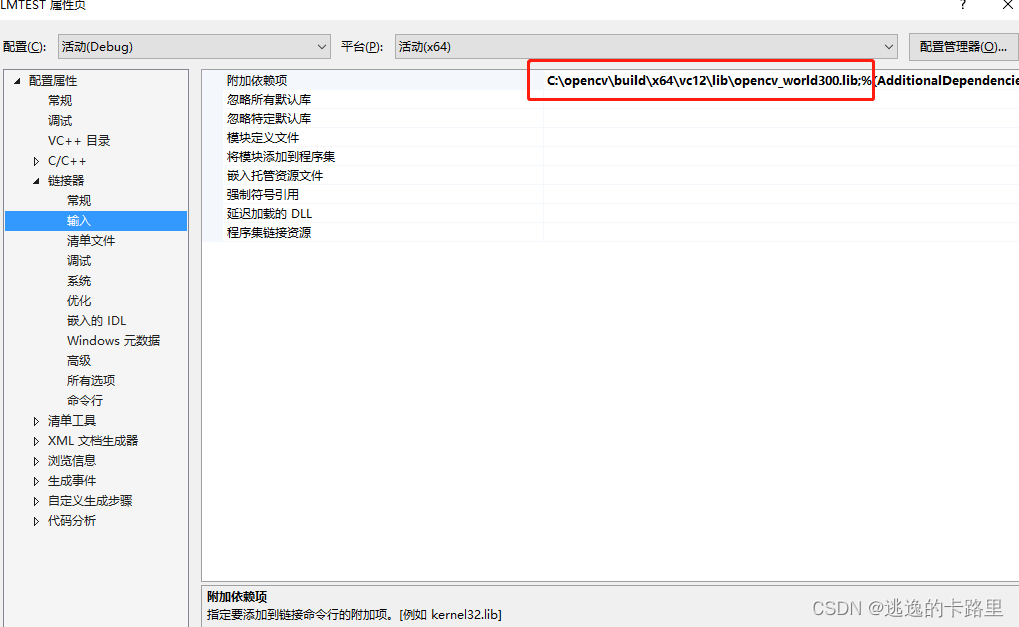
在配置#include <opencv2/core/core.hpp>，这个的时候会遇到一些问题，小伙伴可以在网上自己搜下解决办法，
下面是我再vs2015中设置的截图：电脑上安装两个版本OpenCV，设置有点乱
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/645143.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

华为OD机试之最大N个数与最小N个数的和

华为OD机试之最大N个数与最小N个数的和

最大N个数与最小N个数的和 题目描述 给定一个数组&#xff0c;编写一个函数来计算它的最大N个数与最小N个数的和。你需要对数组进行去重。 说明&#xff1a; 数组中数字范围[0, 1000]最大N个数与最小N个数不能有重叠&#xff0c;如有重叠&#xff0c;输入非法返回-1输入非法返…
阅读更多...
Python之pyecharts的常见用法3-极坐标图-漏斗图

Python之pyecharts的常见用法3-极坐标图-漏斗图

Pyecharts是一个基于Echarts的Python可视化库&#xff0c;可以用Python语言轻松地生成各种交互式图表和地图。它支持多种图表类型&#xff0c;包括折线图、柱状图、散点图、饼图、地图等&#xff0c;并且可以通过简单的API调用实现数据可视化。 Pyecharts的优点包括&#xff1a…
阅读更多...
Python编程入门基础及高级技能、Web开发、数据分析和机器学习与人工智能

Python编程入门基础及高级技能、Web开发、数据分析和机器学习与人工智能

文章目录 入门基础安装 Python 环境&#xff0c;选择一个 IDE&#xff0c;如 PyCharm、VSCode等。学习基本语法&#xff1a;变量、数据类型、条件语句、循环语句、函数、异常处理等。熟悉标准库&#xff1a;常用模块、内置函数等。学习基本的面向对象编程&#xff08;OOP&#…
阅读更多...
Doris数仓的4大特点

Doris数仓的4大特点

01-极简架构 Doris从设计上来说&#xff0c;融合了Google Mesa的数据存储模型、Apache的ORCFile存储格式、Apache Impala查询引擎和MySQL交互协议&#xff0c;是一个拥有先进技术和先进架构的领先设计产品&#xff0c;如图1所示。 ▲图1 Doris技术分解图 在架构方面&#xff…
阅读更多...
Android Binder机制浅谈以及使用Binder进行跨进程通信的俩种方式（AIDL以及直接利用Binder的transact方法实现）

Android Binder机制浅谈以及使用Binder进行跨进程通信的俩种方式（AIDL以及直接利用Binder的transact方法实现）

Binder机制学习 Binder机制是Android进行IPC&#xff08;进程间通信&#xff09;的主要方式Binder跨进程通信机制&#xff1a;基于C/S架构&#xff0c;由Client、Server、ServerManager和Binder驱动组成。 进程空间分为用户空间和内核空间。用户空间不可以进行数据交互&#xf…
阅读更多...
Guitar Pro8.0.1吉他制谱打谱软件

Guitar Pro8.0.1吉他制谱打谱软件

Guitar Pro是一款专业的吉他编曲、打谱软件&#xff0c;Guitar pro的特点是它几乎涵盖了所有的乐谱形式&#xff0c;包括四线谱、五线谱、六线谱等等&#xff0c;最新的Guitar Pro8.1版本还新增了简谱&#xff0c;我们可以在GuitarPro8.1中使用简谱进行演奏。Guitar pro支持在制…
阅读更多...
使用ETL工具Kettle实现，把一个数据库中的多张表的数据同步到另外一个数据库中

使用ETL工具Kettle实现，把一个数据库中的多张表的数据同步到另外一个数据库中

需求&#xff1a;使用ETL工具Kettle实现&#xff0c;把一个数据库中的多张表的数据&#xff08;不少于3张表&#xff09;同步到另外一个数据库中 1》使用Kettle工具连接MySQL数据库&#xff1a;连接第一个数据库db03。出现圈3说明连接成功。 &#xff08;依次点击&#xff1a;…
阅读更多...
webpack处理CSS文件，打包到单独的文件、压缩、以及兼容性处理

webpack处理CSS文件，打包到单独的文件、压缩、以及兼容性处理

一、将css打包到单独的文件 如上图&#xff1a; Css 文件目前被打包到 js 文件中&#xff0c;当 js 文件加载时&#xff0c;会创建一个 style 标签来生成样式 这样对于网站来说&#xff0c;如果网络比较慢的话会出现闪屏现象&#xff0c;用户体验不好 我们去控制台将往速调慢&…
阅读更多...
JDK version和class file version对应关系

JDK version和class file version对应关系

https://docs.oracle.com/javase/specs/jvms/se20/html/jvms-4.html#jvms-4.1 表 4.1-A. 类文件格式主要版本 Java SEReleasedMajorSupported majors1.0.2May 199645451.1February 199745451.2December 19984645 .. 461.3May 20004745 .. 471.4February 20024845 .. 485.0Sept…
阅读更多...
手把手教你实战TDD | 京东云技术团队

手把手教你实战TDD | 京东云技术团队

1. 前言 领域驱动设计&#xff0c;测试驱动开发。 我们在《手把手教你落地DDD》一文中介绍了领域驱动设计&#xff08;DDD&#xff09;的落地实战&#xff0c;本文将对测试驱动开发&#xff08;TDD&#xff09;进行探讨&#xff0c;主要内容有&#xff1a;TDD基本理解、TDD常…
阅读更多...
depcheck检查缺失的或者位使用的依赖

depcheck检查缺失的或者位使用的依赖

depcheck它可以帮助我们找出问题&#xff0c;在 package.json 中&#xff0c;每个依赖包如何被使用、哪些依赖包没有用处、哪些依赖包缺失。它是解决前端项目中依赖包清理问题的一个常用工具 depcheck官方文档地址 Github&#xff1a;https://github.com/depcheck/depcheck 1…
阅读更多...
笔记本触摸板没反应？1分钟，快速解决！

笔记本触摸板没反应？1分钟，快速解决！

案例&#xff1a;在使用笔记本电脑时&#xff0c;我喜欢使用触摸板进行一些电脑上的操作。但是最近我的触摸板突然没反应&#xff0c;不能使用。有小伙伴知道这是什么原因吗&#xff1f;该如何解决呀&#xff1f; 笔记本电脑已经成为我们日常生活和工作中不可或缺的工具。然而…
阅读更多...
光传感芯片产品应用领域解析

光传感芯片产品应用领域解析

光传感产品主要应用于穿戴心率等健康检测、安防环境光监测、智能家居环境光感测、智慧电子产品自动控制、工业自动控制及安全检查、控制。 WH光感材料特点&#xff1a; 1、双波普独立通道&#xff0c;独立控制 2、波谱响应波长可客制化定制&#xff1a; —环境光红蓝绿、光距感…
阅读更多...
企业邀请媒体报道活动，邀请本地媒体好，还是全国性的媒体好

企业邀请媒体报道活动，邀请本地媒体好，还是全国性的媒体好

传媒如春雨&#xff0c;润物细无声&#xff0c;大家好&#xff0c;我是51媒体网胡老师。 企业做活动在制定媒体策略&#xff0c;媒体传播规划的时候&#xff0c;往往不知道改如何选择&#xff0c;今天胡老师就来分享下本地媒体和全国性媒体的特点&#xff0c;帮助大家更好的制…
阅读更多...
SpringCloud搭建Eureka服务注册中心(六)

SpringCloud搭建Eureka服务注册中心(六)

前面说过eureka是c/s模式的 server服务端就是服务注册中心&#xff0c;其他的都是client客户端&#xff0c;服务端用来管理所有服务&#xff0c;客户端通过注册中心&#xff0c;来调用具体的服务&#xff1b; 我们先来搭建下服务端&#xff0c;也就是服务注册中心&#xff1b…
阅读更多...
uniapp小程序订阅消息推送+Thinkphp5后端代码教程示例

uniapp小程序订阅消息推送+Thinkphp5后端代码教程示例

记录一下通过uniapp开发小程序消息推送的实例&#xff0c;配合后端tp推送&#xff0c;之前写的项目是微信小程序而且后端是原生php&#xff0c;这次通过项目记录一下 目录 回顾access_token获取规则以及思路 第一步&#xff1a;设计前端触发订阅事件第二步&#xff1a;设计将to…
阅读更多...
1140道Java常见面试题及详细答案

1140道Java常见面试题及详细答案

最近感慨面试难的人越来越多了&#xff0c;一方面是市场环境&#xff0c;更重要的一方面是企业对 Java 的人才要求越来越高了。 基本上这样感慨的分为两类人&#xff1a; 第一&#xff0c;虽然挂着 3、5 年经验&#xff0c;但肚子里货少&#xff0c;也没啥拿得出手的项目&#…
阅读更多...
OPNET出现“Packet pointer references unowned packet(＜pk_id＞)”错误的解决办法

OPNET出现“Packet pointer references unowned packet(＜pk_id＞)”错误的解决办法

在使用 OPNET Modeler 软件时&#xff0c;会遇到很多奇奇怪怪的报错&#xff0c;今天要介绍的报错内容如下。 Packet pointer references unowned packet(<pk_id>). 程序中断的原因截图如下图所示。 由上图可以看到&#xff0c;引发错误的 OPNET 核心函数是 op_pk_send(…
阅读更多...
快速幂应用之剪绳子问题

快速幂应用之剪绳子问题

有这样一类问题&#xff0c;给你一个长度为n的绳子&#xff0c;要求你可以剪切任意次数&#xff0c;分为任意段&#xff0c;使得这些子段长度的乘积最大。我们把这类问题暂时先称为剪绳子&#xff0c;这种问题的解法也很简单&#xff0c;通过数学证明可以得出&#xff0c;我们优…
阅读更多...
​Java容器的继承关系​

​Java容器的继承关系​

Java容器的继承关系 Collection接口 Collection接口中所定义的方法 int size(); boolean isEmpty(); void clear(); boolean contains(Object element);//是否包含某个对象 boolean add(Object element); Iterator iterator(); boolean containsAll(Collection c);//是否包含另…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023