题目描述

给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个表达式：
例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。

示例 1：
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：
输入：nums = [1], target = 1
输出：1

遍历

class Solution {
    int res;
    int target_sum;
    public int findTargetSumWays(int[] nums, int target) {
        target_sum = target;
        dfs(0,nums,0);
        return res;
    }


    void dfs(int layer, int[] nums, int cur_value) {
        if(layer == nums.length) {
            if(cur_value == target_sum) res++;
            return;
        }
        dfs(layer + 1,nums,cur_value + nums[layer]); 
        dfs(layer + 1,nums,cur_value - nums[layer]); 
    }
}

动态规划

https://leetcode.cn/problems/target-sum/solution/mu-biao-he-by-nehzil-x5am/
当目标和为target时，设nums中所有整数和为sum，某个和为target的序列中的正数和为p，负数绝对值和的为n，可以推导出：
target = p - n
sum = p + n
target = p - (sum - p)
target = 2p - sum
等价于 p = (target + sum) / 2

此时我们的问题转换 为从nums中选取m个数，能使其和为 (target + sum) / 2 。返回满足条件组合的个数。

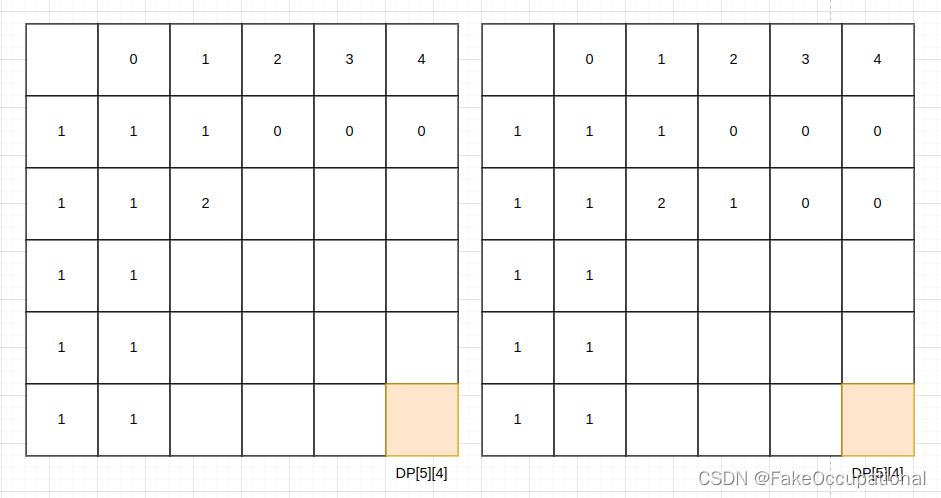
在这里插入图片描述

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        /* 在进行动态规划算法之前需要进行下面的判断和计算 */
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        int diff = sum - target;
        if (diff < 0 || diff % 2 != 0) {
            return 0;
        }
        int n = nums.size();
        int neg = diff / 2;
        /* 定义dp数组 */
        vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
        /* dp数组初始化 */
        dp[0][0] = 1;
        /* 遍历 */
        for (int i = 1; i <= n; i++) {// 先遍历物品
            for (int j = 0; j <= neg; j++) { // 在遍历背包容量，二维和j的顺序无关，for (int j = neg; j >= 0; j--)也行
                dp[i][j] = dp[i - 1][j];
                /* 如果背包剩余j的容量大于放的物品nums[i-1]则就可以将物品nums[i-1]放入背包中 */
                if (j >= nums[i - 1]) {
                    dp[i][j] += dp[i - 1][j - nums[i - 1]];
                }
            }
        }
        return dp[n][neg];
    }
};

// 作者：Nehzil
// 链接：https://leetcode.cn/problems/target-sum/solution/mu-biao-he-by-nehzil-x5am/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

维度压缩的code

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        /* 在进行动态规划算法之前需要进行下面的判断和计算 */
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        int diff = sum - target;
        if (diff < 0 || diff % 2 != 0) {
            return 0;
        }
        int n = nums.size();
        int neg = diff / 2;
        /* 定义dp数组 */
        vector<int> dp( vector<int>(neg + 1));
        /* dp数组初始化 */
        dp[0] = 1;
        /* 遍历 */
        for (int i = 1; i <= n; i++) {// 先遍历物品
            for (int j = neg; j >= 0; j--) { // 在遍历背包容量
                // dp[i][j] = dp[i - 1][j];
                /* 如果背包剩余j的容量大于放的物品nums[i-1]则就可以将物品nums[i-1]放入背包中 */
                if (j >= nums[i - 1]) {
                    dp[j] += dp[j - nums[i - 1]];
                }
            }
        }
        return dp[neg];
    }
};