提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

第二类曲线积分

因为之前学习第二类曲线的时候，不是很理解；所以最近看了mit的多元微积分课程，做一些课程笔记。

一、向量场是什么？

示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。
理解第二类曲线积分的前置知识点是：向量场。
可以用这样的函数表示向量场：
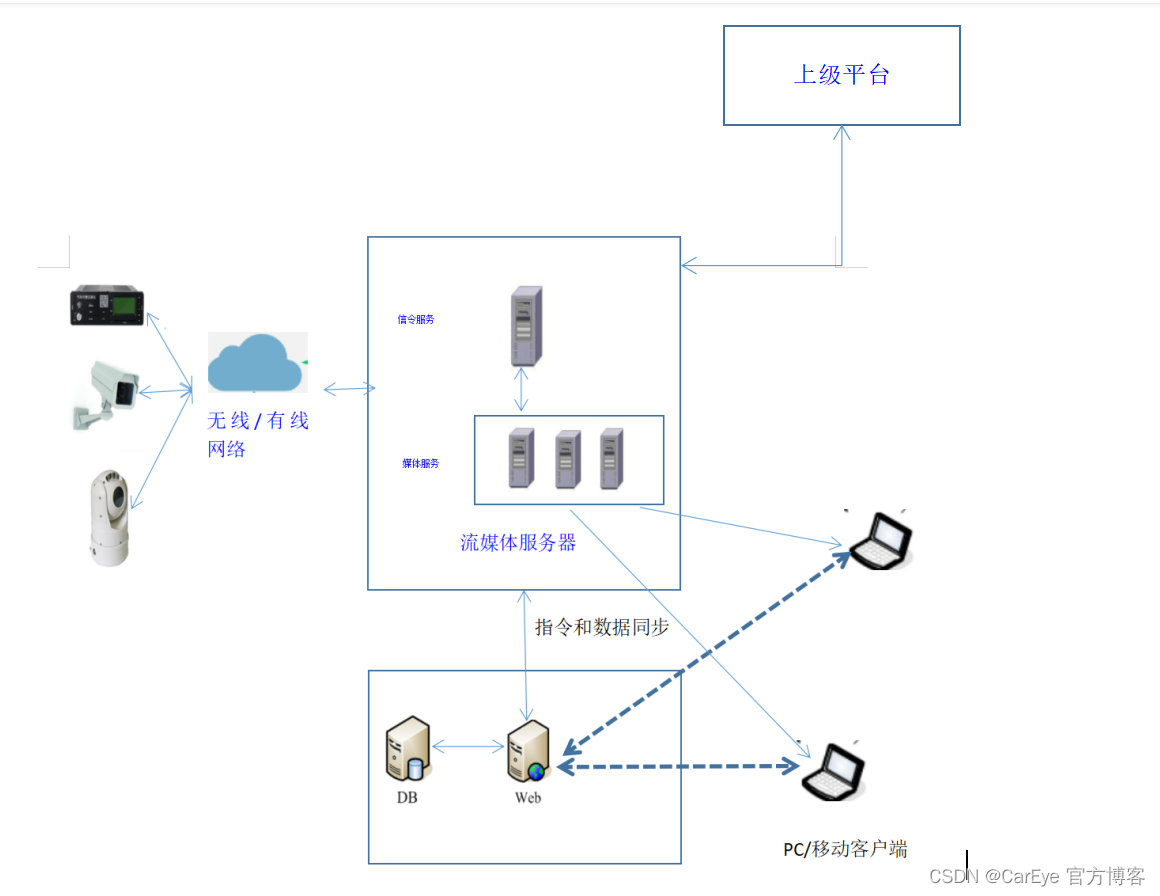
$$\mathbf{F}(x,y)=M(x,y)\mathbf{i}+N(x,y)\mathbf{j}$$
注意该方程里的i, j表示的是向量。

二、向量场可视化

可以方便理解向量场，可以可视化向量场。通过搜索工具可以知道matplotlib的quiver可以做这件事。
$$\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}$$

# Import required modules
import numpy as np
import matplotlib.pyplot as plt

# Meshgrid
x, y = np.meshgrid(np.linspace(-5, 5, 10),
				np.linspace(-5, 5, 10))

# Directional vectors
u = -y
v = x

# Plotting Vector Field with QUIVER
plt.quiver(x, y, u, v, color='g')
plt.title('Vector Field')

# Show plot with grid
plt.grid()
plt.show()

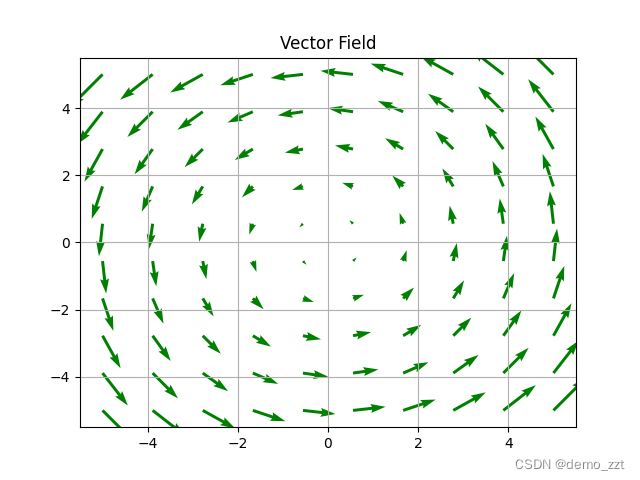
通过图片可以理解，向量场中每个位置存在一个确定的向量。

三、计算

有一个很经典的物理问题，给定一个确定的曲线C，计算在这个向量场内的做功问题。

$$W={\int }_C\vec{F}d\vec{r}=\underset{\Delta r_i\to 0}{\lim }{\Sigma }_i\vec{F}\Delta \overrightarrow{r_i}=\underset{\Delta r_i\to 0}{\lim }{\Sigma }_i\vec{F}\frac{\Delta \vec{r}}{\Delta t}\Delta t$$

1. 计算方式一

向量场F
$$\vec{F}=-y\vec{i}+x\vec{j}$$
曲线C
$$\{\begin{array}{c}x=t\\ y=t^2\end{array}0<t<1$$
计算
$${\int }_C\vec{F}d\vec{r}=\int \vec{F}\frac{d\vec{r}}{dt}dt=\int <-t^2,t>\ast <1,2t>dt=\int t^{2}dt$$

2. 计算方式二

$$\begin{gathered} \vec{F}=<M,N> \\ d\vec{r}=<dx,dy> \\ {\int }_C\vec{F}d\vec{r}={\int }_{C}Mdx+Ndy \end{gathered}$$
$$\begin{gathered} x=t\Rightarrow dx=dt \\ y=t^2\Rightarrow dy=2tdt \\ {\int }_C\vec{F}d\vec{r}={\int }_C-ydx+xdy={\int }_C-t^{2}dt+t\ast 2tdt=\int t^{2}dt \end{gathered}$$