​👻内容专栏：《数据结构与算法篇》
🐨本文概括： 讲述排序的概念、直接插入排序、希尔排序、插入排序和希尔排序的区别。
🐼本文作者：花 碟
🐸发布时间：2023.6.13

一、排序的概念及其运用

1.1 排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

1.2 排序的运用

生活中的运用排序有很多例子，比如在我们拿起手机打开美团app点外卖时，手机顶栏有综合排序/配送费/好评率等选项，用户点击之后，系统就会进行从高到低，或者从低到高进行排序；在全国上千所高校中，在百度中进行搜索排名，系统会按综合排序对高校进行排序……

二、直接插入排序

2.1 基本思想

直接插入排序是一种简单的插入排序法，其基本思想是：
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

🧾实际中我们玩扑克牌时，就用到了插入排序的思想：

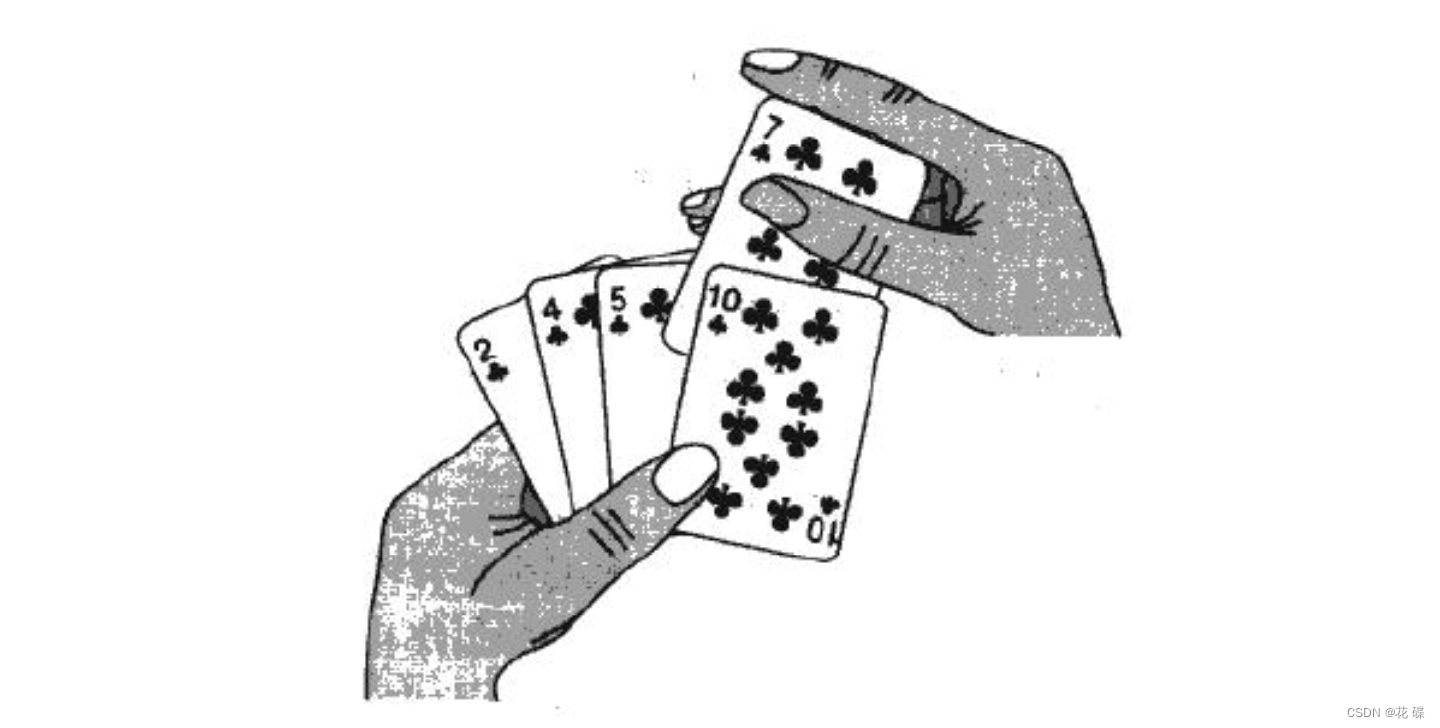
2.2 直接插入排序

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]与array[i-1],array[i-2],…的顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。

📌👇直接插入排序的特性总结：

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

2.3 代码实现

插入一个数的前提必须是保证前面区间的数据是有序的(注意当只有一个数时，本来就可以看作是有序的)，插入完之后，使新序列仍然有序。假设把下面图中乱序的数组排成升序来说，[0，end]的区间数据是有序的 ，end默认为下标0开始，end + 1为下标的元素即为即将被插入的数据，为了避免后面被覆盖，我们需要提前保存到tmp变量当中。如果a[end]大于tmp，就将a[end] 放入到tmp的位置，然后end–，去找前一个有序中的元素，如果前一个元素不存在，也就是end走到了-1，此时tmp就直接插入到下标为0的位置，这是第一种插入的情况（end在有序序列中已经走完了，tmp插入序列中第一个位置）。第二种插入的情况是（tmp在序列中找到了合适的位置插入），即a[end] 小于tmp，tmp插入到a[end + 1]的位置。

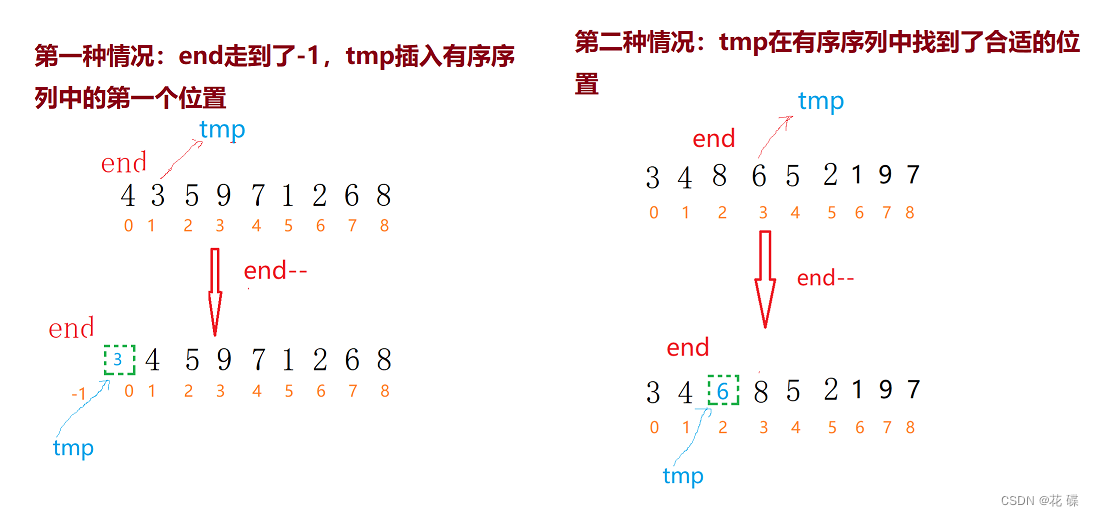
而这两种情况可以进行合并，因为都是将tmp放入到end后面的位置，具体请看以下代码👇

//直接插入排序
void InsertSort(int* a, int n)
{
	//确定区间 一共需要排的数据,注意：end要小于等于n - 2,否则tmp会出现越界访问
	for (int i = 0; i < n - 1;i++)
	{
		int end = i;
		//[0, end] 有序，插入一个tmp 使[0,end + 1]的数据仍然有序
		int tmp = a[end + 1];//要插入的数据需要提前存储，否则会被覆盖
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				//当a[end] < tmp 跳出循环
				break;
			}
		}
		//1.end走到了-1
		//2.a[end] < tmp
		a[end + 1] = tmp;
	}
}

2.4 插入排序时间复杂度

⏱️时间复杂度：序列想要排列成升序，如果原序列是逆序，时间复杂度最坏，时间复杂度为O(N²)
如果原序列是升序，那么此时时间复杂度情况是最好的，时间复杂度为O(N)

三、希尔排序

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。
👉插入排序是一种简单实用的排序算法，适用于小规模数据或基本有序的数据集。但对于大规模乱序的数据集，性能较差，其时间复杂度为O(N²)，为了弥补插入排序的效率缺陷，下面让我们就来学习希尔排序的具体实现过程吧👇

3.1 希尔排序(缩小增量排序)

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

3.2 基本思想

😉😉简单来说，其核心思想分为两步：👇

1. 分割为若干组，进行多组预排序
2. 最后进行一次插入排序

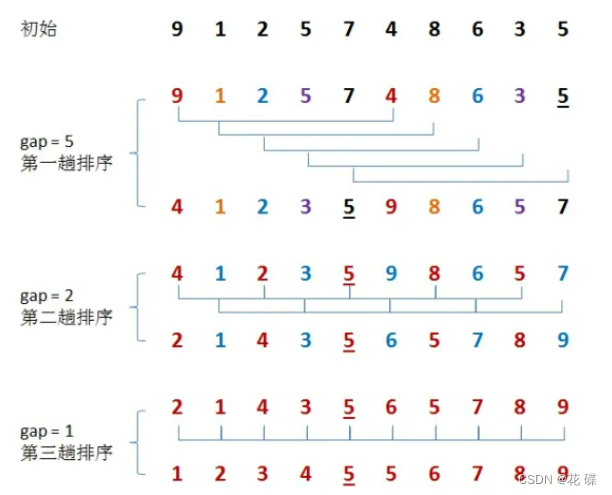
假设我们把原始序列分为gap组，（gap与数组的大小有关，并没有一个合适的值，后面会具体谈论gap如何给值）。这里拿图中的原始序列来看，为了是方便大家更容易理解，把gap暂定为3.
间隔为gap，也就是3的为同一组，分别由红色线、蓝色线、绿色线三部分组成，对这三个组进行预排序，此时需要注意的是被插入的数据不是end后面紧跟的数据，而是 end + gap 为下标的数据，每一组都是如此，那么控制end的结束条件是什么呢？答案是一定要小于 n - gap ，如果一旦等于 n - gap ，插入的数据就会访问到下标为n的位置，此时就出现越界访问了！

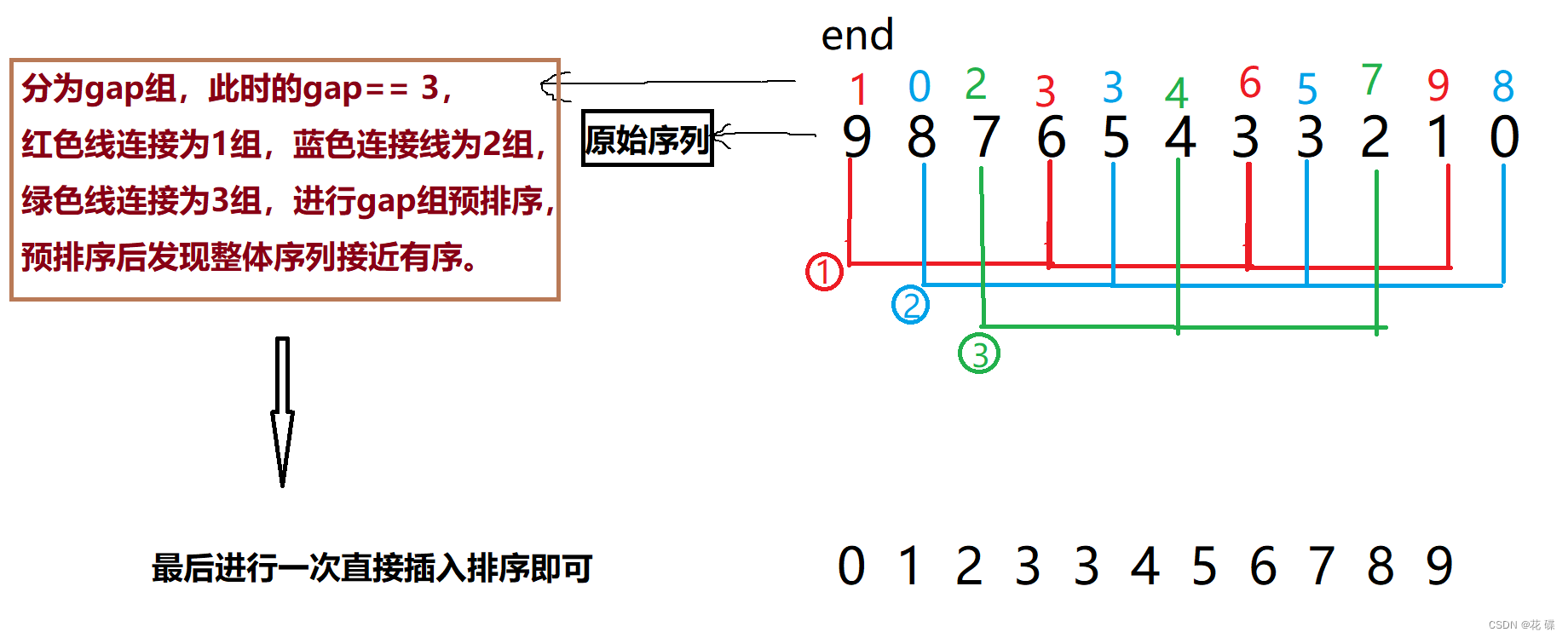
🥰🥰下面我们就根据这个思路，把预排序的代码给写下来👇：

//gap组数据排序
// j == 0 排红色组
// j == 1 排蓝色组
// j == 2 排绿色组
for (int j = 0; j < gap; j++)
{
	//预排序 注意条件，end的区间范围一定小于n - gap
	for (int i = 0; i < n - gap; i += gap)
	{
		int end = i;
		int tmp = a[end + gap];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + gap] = a[end];
				end -= gap;
			}
			else
			{
				break;
			}
		}
		a[end + gap] = tmp;
	}
}

😜😜我们可以换一种方式写，这种代码是将gap组数据并排👇：

注⚠️：1.这种方式与上一种方式效率是一样的，并不存在循环少一个效率就更高效了。
2.上一种是排完一组接着排下一组，以下这种是gap组进行合并一起排序。

//gap组并排
	for (int i = 0; i < n - gap; i++)
	{
		int end = i;
		int tmp = a[end + gap];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + gap] = a[end];
				end -= gap;
			}
			else
			{
				break;
			}
		}
		a[end + gap] = tmp;
	}

观察以下图中，gap的变化：

💡我们发现：

1. gap越大，越大的数能够较快的挪动到最后面的位置，越小的数能够较快的挪动到最前面的位置。由于较大的间隔可以跳跃式地比较和交换元素，可以在较少的比较和交换操作下完成一轮排序，从而提高排序速度。
2. gap越小，较小的间隔能够处理部分有序的数据集和改善最后一轮排序，但总体比较和交换的次数会越多。

这里大家是不是更容易理解了很多。

现在，我们回到刚开始的问题，gap(间隔)该如何确定呢？

• 最早提出的希尔排序使用的是希尔原始增量序列，即使用 N/2 作为初始间隔，然后每次将间隔折半，直到间隔为1。例如，对于一个长度为10的序列，初始间隔为5，然后依次为5/2=2、2/2=1。除了gap / 2 ，Knuth增量序列提出的gap = gap / 3 + 1 也是挺厉害的。还有更多的增量序列，像Hibbard增量序列、Sedgewick增量序列等都是根据经验和实验得出的，目的是让希尔排序在不同情况下都能够有较好的性能表现。具体选择哪种间隔序列取决于具体的应用场景和数据特点。
  一般来说，较大的间隔能够快速减小序列的规模，而较小的间隔能够更好地处理部分有序的数据集。因此，一种常见的做法是结合多种间隔序列，先使用较大的间隔进行排序，然后逐渐缩小间隔直到最后一次使用间隔为1进行最后的排序。
• 虽然不同的间隔序列会对排序的效率产生影响，但希尔排序的时间复杂度仍然是一个开放问题，至今没有找到一个确定的最优间隔序列。因此，选择合适的间隔序列是一个经验性的问题，需要根据具体情况进行尝试和调整。

所以，我们当今学习，只需要站在巨人的肩膀上往前走，不必自己再去深造轮子😉，ok，下面将希尔排序的代码放置下面。

3.3 代码实现

//希尔排序
void ShellSort(int* a, int n)
{

	int gap = n;
	while (gap > 1)
	{
		//进行多次预排序，加上最后一组直接插入排序。
		gap = gap / 3 + 1;
		//gap = gap / 2;
		
		 //gap组并排
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

3.4 希尔排序时间复杂度

希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，
这里借用《数据结构-用面相对象方法与C++描述》书中的一段描述：

目前对于gap的取值，咱们都是站在巨人的肩膀上学习，Knuth进行了大量的试验统计，以我们的数学知识证明还是挺困难的，如果数学功底好的小伙伴可以自己试着证明一下，所以这里我们暂时就按照：O(N^1.25)到O(1.6 * N^1.25)来算。

四、总结

总结一下，插入排序和希尔排序的区别主要在以下几个方面：

思想：插入排序将待排序序列看作是已排序和未排序两部分，逐个插入元素；而希尔排序通过分组的方式，对整个序列进行多次插入排序。
效率：希尔排序相对于插入排序来说，可以在某些情况下更快地完成排序，尤其是对于大规模数据集。直接插入排序呢，如果待排序的数据集基本有序或者小规模，插入排序的性能较好。
稳定性：插入排序是稳定的排序算法，相等元素的相对位置在排序后不会改变。然而，当希尔排序涉及到跳跃式移动元素时，改变了元素的相对位置，是不稳定的。

🥰🥰本章节完，后续会补充二叉树进阶内容知识，小伙伴们可以持续关注，若本篇文章对你有帮助的话，可以三连支持博主哦~，另外本篇内容有编写有误的话，可以私聊博主进行纠正！