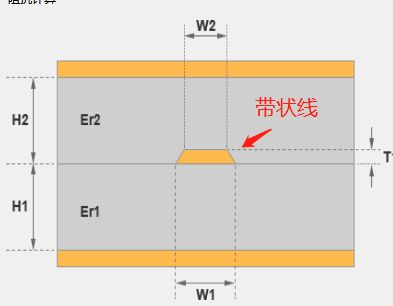
晶体热学性能研究的方法：第一性原理声子谱计算

第一性原理声子谱计算是一种基于量子力学的计算方法，用于研究物质中声子的性质和行为。声子是晶体中的量子态，它描述了晶体中原子振动的性质。声子谱计算可以提供关于晶体结构、热力学性质、相变等方面的重要信息，对于理解和设计材料的性能至关重要。

声子谱计算的核心是基于第一性原理的密度泛函理论（DFT）。密度泛函理论是一种基于电子密度的理论框架，可以用于描述多电子体系的基态性质。在声子谱计算中，首先需要进行基于DFT的电子结构计算，得到晶体的电子能带结构和电子密度分布。这些信息对于声子谱计算是至关重要的，因为声子与电子之间存在相互作用。

在声子谱计算中，声子的运动方程可以通过Hooke定律和Born-Oppenheimer近似推导得到。Hooke定律描述了原子之间的力常数，而Born-Oppenheimer近似则假设电子和声子的运动可以分开考虑。通过求解声子的运动方程，可以得到声子的能量和动量，从而获得声子谱。

为了解决声子运动方程，需要引入周期性边界条件，并对晶体的原子进行微小的扰动，例如将一个原子稍微移动一点。然后，通过求解运动方程，可以得到晶体中所有声子的能量和波矢。这些能量和波矢的组合就构成了声子谱。

实际进行声子谱计算时，有几种常用的方法。一种常见的方法是密度泛函微扰论（DFPT），它基于线性响应理论，通过微小的外势扰动来计算声子谱。另一种方法是有限差分法，它将运动方程转化为离散的差分方程，然后通过数值求解得到声子谱。

声子谱计算的结果可以用于解释实验观测，例如红外光谱、拉曼光谱等。声子谱提供了关于晶体中振动模式的信息，包括频率、强度和偏振等。这些信息对于理解晶体的结构稳定性、热导率、热膨胀等热力学性质非常重要。

测试狗模拟计算