【1687. 从仓库到码头运输箱子】

来源：力扣（LeetCode）

描述：

你有一辆货运卡车，你需要用这一辆车把一些箱子从仓库运送到码头。这辆卡车每次运输有 箱子数目的限制 和 总重量的限制 。

给你一个箱子数组 boxes 和三个整数 portsCount, maxBoxes 和 maxWeight ，其中 boxes[i] = [portsi, weighti] 。

portsi 表示第 i 个箱子需要送达的码头， weightsi 是第 i 个箱子的重量。
portsCount 是码头的数目。
maxBoxes 和 maxWeight 分别是卡车每趟运输箱子数目和重量的限制。

箱子需要按照 数组顺序 运输，同时每次运输需要遵循以下步骤：

卡车从 boxes 队列中按顺序取出若干个箱子，但不能违反 maxBoxes 和 maxWeight 限制。
对于在卡车上的箱子，我们需要 按顺序 处理它们，卡车会通过 一趟行程 将最前面的箱子送到目的地码头并卸货。如果卡车已经在对应的码头，那么不需要 额外行程 ，箱子也会立马被卸货。
卡车上所有箱子都被卸货后，卡车需要 一趟行程 回到仓库，从箱子队列里再取出一些箱子。
卡车在将所有箱子运输并卸货后，最后必须回到仓库。

请你返回将所有箱子送到相应码头的 最少行程 次数。

示例 1：

输入：boxes = [[1,1],[2,1],[1,1]], portsCount = 2, maxBoxes = 3, maxWeight = 3
输出：4
解释：最优策略如下：
- 卡车将所有箱子装上车，到达码头 1 ，然后去码头 2 ，然后再回到码头 1 ，最后回到仓库，总共需要 4 趟行程。
所以总行程数为 4 。
注意到第一个和第三个箱子不能同时被卸货，因为箱子需要按顺序处理（也就是第二个箱子需要先被送到码头 2 ，然后才能处理第三个箱子）。

示例 2：

输入：boxes = [[1,2],[3,3],[3,1],[3,1],[2,4]], portsCount = 3, maxBoxes = 3, maxWeight = 6
输出：6
解释：最优策略如下：
- 卡车首先运输第一个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第二、第三、第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五个箱子，到达码头 3 ，回到仓库，总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。

示例 3：

输入：boxes = [[1,4],[1,2],[2,1],[2,1],[3,2],[3,4]], portsCount = 3, maxBoxes = 6, maxWeight = 7
输出：6
解释：最优策略如下：
- 卡车运输第一和第二个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第三和第四个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五和第六个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。

示例 4：

输入：boxes = [[2,4],[2,5],[3,1],[3,2],[3,7],[3,1],[4,4],[1,3],[5,2]], portsCount = 5, maxBoxes = 5, maxWeight = 7
输出：14
解释：最优策略如下：
- 卡车运输第一个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第二个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第三和第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第六和第七个箱子，到达码头 3 ，然后去码头 4 ，然后回到仓库，总共 3 趟行程。
- 卡车运输第八和第九个箱子，到达码头 1 ，然后去码头 5 ，然后回到仓库，总共 3 趟行程。
总行程数为 2 + 2 + 2 + 2 + 3 + 3 = 14 。

提示：

1 <= boxes.length <= 10⁵
1 <= portsCount, maxBoxes, maxWeight <= 10⁵
1 <= portsi <= portsCount
1 <= weightsi <= maxWeight

方法：动态规划 + 单调队列优化

前言

为了叙述方便，我们记箱子的数量为 n，它们的目的地分别为 p₁ , ⋯ , p_n ，重量分别为 w₁ ,⋯ ,w_n 。

记 W_i 表示 w 的前缀和，即：

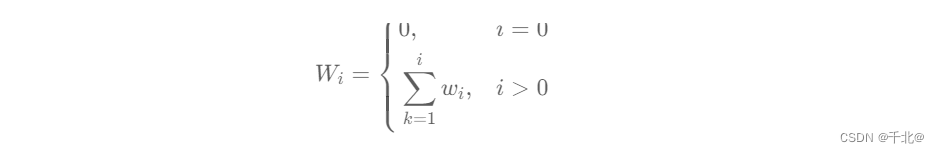
这样我们可以用 W_i − W_j−1 方便地表示第 i 个到第 j 个箱子的重量，并与 maxWeight 进行比较。

记示性函数 I(i) 表示 p_i 和 p_i+1 是否不等，即：

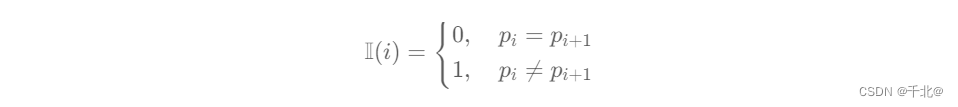
记 neg(i, j) 表示 p_i, ⋯ , p_j 相邻两项不等的次数，即：

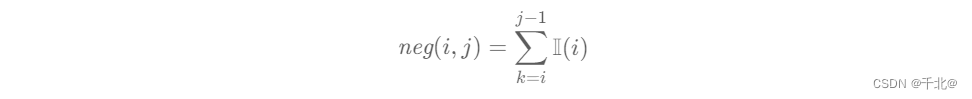
这样我们可以用 neg(i, j) + 2 方便地求出一次性运送第 i 个到第 j 个箱子需要的行程次数，这里的 +2 表示来回需要的 2 次。

为了便于快速计算 neg(i, j) ，我们也可以使用前缀和的方式进行存储。记 neg_i = neg(1, i) 表示前缀和，那么 neg(i, j) = neg_j − neg_i 可以在 O(1) 的时间求出。

注意：这里是 neg_j − neg_i 而不是 neg_j − neg_i-1 ，读者可以思考一下其原因。

思路与算法

我们可以使用动态规划解决本题。

记 f_i 表示运送前 i 个箱子需要的最少行程次数，这里的「前 i 个箱子」指的是目的地为 p₁, ⋯ , p_i 的 i 个箱子。我们可以写出状态转移方程：

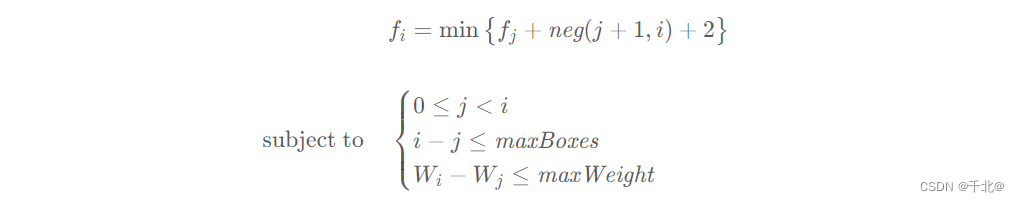
即枚举上一次运送的最后一个箱子为 j（这里的 j 可以为 0，表示这一次是第一次运送箱子），那么这一次运送的箱子为 [j + 1, i] 。箱子的数量不超过 maxBoxes ，重量之和不能超过 maxWeight 。运送的行程次数即为 p_j+1, ⋯ , p_i 相邻两项不等的次数 neg(j + 1, i) 加上来回的 2 次。

边界条件为 f₀ = 0 ，最终答案即为 f_n 。

优化

然而上述动态规划的时间复杂度为 O(n²) ，我们需要进行优化。我们将 neg(j + 1, i) 拆分成两个前缀和的差，即：

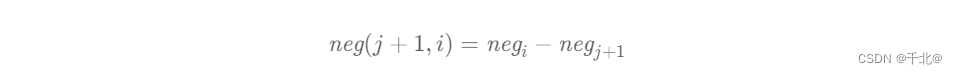
带入原状态转移方程：

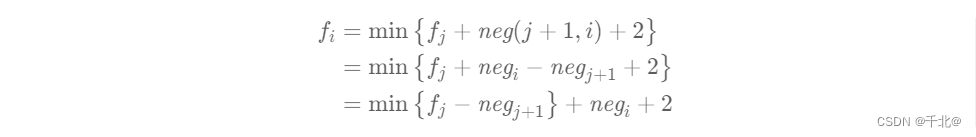
由于 neg_i 和 2 都是与 j 无关的项，因此可以从 min⁡{⋅} 中提取出来。

记 g_j = f_j − neg_j+1 ，状态转移方程即为：

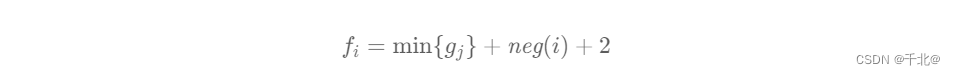
如果只有 0 ≤ j < i 的限制条件，那么我们实时维护 g_j 的最小值进行 O(1) 的转移即可。但现在有 i − j ≤ maxBoxes 这两个额外的限制条件，最小的 g_j 对应的 j 不一定满足限制。

我们可以将两个额外的限制看成：

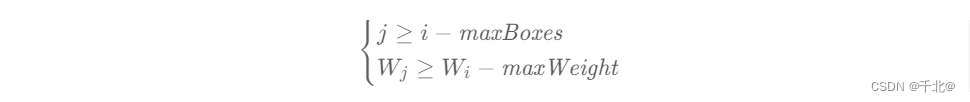
注意到两个不等式右侧的值都是随着 i 的递增而递增的，因此如果当 i = i₀ 时，某个 j₀ 不满足不等式限制，那么当 i > i₀时，j₀将永远不可能重新满足条件。

因此我们就可以使用单调队列对动态规划进行优化，对于两个可以进行转移的 g_j0 和 g_j1，在 j₀ < j₁的前提下：

如果 g_j0 < g_j1，那么我们需要将 g_j0 和 g_j1 都保留下来，这是因为当 g_j0 还满足限制时， g_j0 比 g_j1 更优；而当 g_j0 不满足限制后，g_j1 可能会代替 g_j0，成为新的最优转移；
如果 g_j0 ≥ g_j1，那么我们只需要将 g_j1 保留下来即可。这是因为当 g_j0 还满足限制时，选择 g_j1 并不会更差，并且 g_j1 可以满足限制的时间（即随着 i 的递增）更久。

因此，我们使用一个队列存储所有需要被保留的 g_j（存储下标 j 即可），从队首到队尾，j 的值单调递增，g_j 的值也单调递增。在进行状态转移求解 f_i 时：

首先我们不断从队首弹出元素，直到队首的 j 是满足额外限制的；
使用队首的 j 进行转移，得到 f_i；
计算出 g_i，并不断从队尾弹出元素，直到队列为空或者队尾元素对应的 g 值严格小与g_i；
将 g_i 放入队列。

状态转移需要的时间为 O(1)。而对于单调队列的部分，每一个 g_i 会被加入队列恰好一次，并且被从队列中弹出最多一次，因此均摊时间为 (1)。这样一来，动态规划的时间复杂度降低为 O(n)。

代码:

代码中很多变量都是为了和文字部分保持一致而添加的，如果熟练了掌握了本题使用的方法，可以优化掉一些变量。

class Solution {
public:
    int boxDelivering(vector<vector<int>>& boxes, int portsCount, int maxBoxes, int maxWeight) {
        int n = boxes.size();
        vector<int> p(n + 1), w(n + 1), neg(n + 1);
        vector<long long> W(n + 1);
        for (int i = 1; i <= n; ++i) {
            p[i] = boxes[i - 1][0];
            w[i] = boxes[i - 1][1];
            if (i > 1) {
                neg[i] = neg[i - 1] + (p[i - 1] != p[i]);
            }
            W[i] = W[i - 1] + w[i];
        }
        
        deque<int> opt = {0};
        vector<int> f(n + 1), g(n + 1);
        
        for (int i = 1; i <= n; ++i) {
            while (i - opt.front() > maxBoxes || W[i] - W[opt.front()] > maxWeight) {
                opt.pop_front();
            }
            
            f[i] = g[opt.front()] + neg[i] + 2;
            
            if (i != n) {
                g[i] = f[i] - neg[i + 1];
                while (!opt.empty() && g[i] <= g[opt.back()]) {
                    opt.pop_back();
                }
                opt.push_back(i);
            }
        }
        
        return f[n];
    }
};