💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文献

---

💥1 概述

文献来源：

 本文综述了连续非线性动力系统噪声时间序列测量中参数和未观测到的轨迹分量的估计问题。首先表明，在没有明确考虑测量误差的参数估计技术（如回归方法）中，噪声测量会产生不准确的参数估计。另一个问题是，对于混沌系统，必须最小化以估计状态和参数的成本函数非常复杂，以至于常见的优化例程可能会失败。我们表明，包含有关潜在轨迹的时间连续性的信息可以显着改善参数估计。本文详细描述了两种同时考虑变量误差问题和复杂成本函数问题的方法：射击方法和递归估计技术。两者都在数值示例中进行了演示。

📚2 运行结果

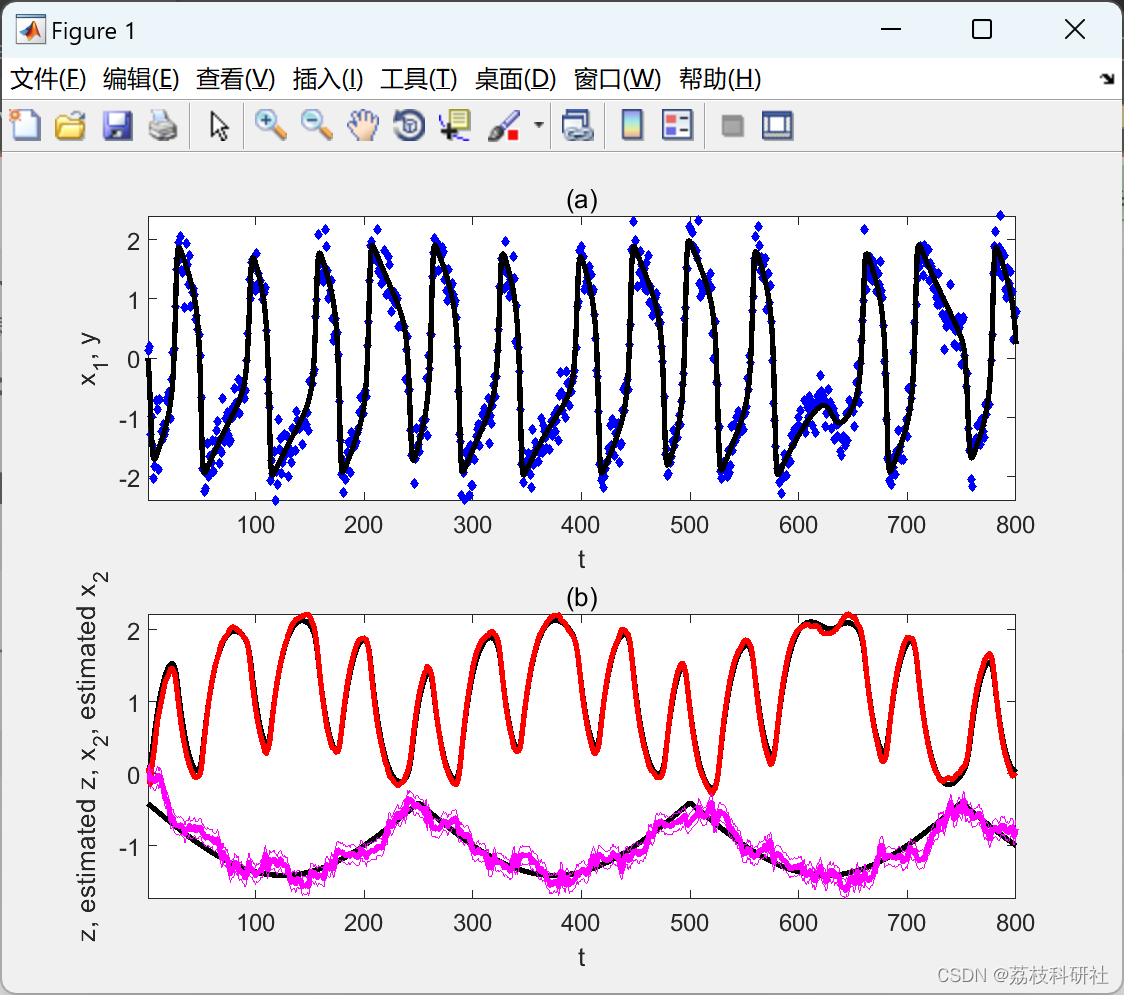
部分代码：

% Simulating data: %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

x0=zeros(2,ll); x0(:,1)=[0; 0]; % true trajectory
dt=.1*dT; nn=fix(dT/dt); % the integration time step is smaller than dT

% External input, estimated as parameter p later on:
z=(1:ll)/250*2*pi; z=-.4-1.01*abs(sin(z/2));

% 4th order Runge-Kutta integrator for FitzHugh-Nagumo system with external input:
for n=1:ll-1;
    xx=x0(:,n);
    for i=1:nn
        k1=dt*FitzHughNagumo_int(xx,z(n));
        k2=dt*FitzHughNagumo_int(xx+k1/2,z(n));
        k3=dt*FitzHughNagumo_int(xx+k2/2,z(n));
        k4=dt*FitzHughNagumo_int(xx+k3,z(n));
        xx=xx+k1/6+k2/3+k3/3+k4/6;
    end;
    x0(:,n+1)=xx;
end;

x=[z; x0]; % augmented state vector (notation a bit different to paper)

R=.2^2*var(FitzHughNagumo_obsfct(x))*eye(dy,dy); % observation noise covariance matrix
rng('default'); rng(0)
y=FitzHughNagumo_obsfct(x)+sqrtm(R)*randn(dy,ll); % noisy data

FitzHughNagumo_fct(dq,x); % this is just to suppress an erroneous warning and otherwise has no function

% Initial conditions %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

xhat=zeros(dx,ll);
xhat(:,2)=x(:,2); % first guess of x_1 set to observation

Q=.015; % process noise covariance matrix

Pxx=zeros(dx,dx,ll);
Pxx(:,:,1)=blkdiag(Q,R,R);

errors=zeros(dx,ll);
Ks=zeros(dx,dy,ll);  % Kalman gains

% Main loop for recursive estimation %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for k=2:ll
    
    [xhat(:,k),Pxx(:,:,k),Ks(:,:,k)]=ut(xhat(:,k-1),Pxx(:,:,k-1),y(:,k),'FitzHughNagumo_fct','FitzHughNagumo_obsfct',dq,dx,dy,R);
    
    Pxx(1,1,k)=Q;
    
    errors(:,k)=sqrt(diag(Pxx(:,:,k)));
    
end; % k

% Results %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

chisq=mean((x(1,:)-xhat(1,:)).^2+(x(2,:)-xhat(2,:)).^2+(x(3,:)-xhat(3,:)).^2);
disp(['Chi square = ',num2str(chisq)]);

% Showing last estimated parameter, used for example for the final estimate of a constant parameter:
% est=xhat(1:dq,ll)'; disp(['Estimated x = ' num2str(est)]);
% error=errors(1:dq,ll)'; disp(['Error = ' num2str(error)]);

figure(1)

subplot(2,1,1)
plot(y,'bd','MarkerEdgeColor','blue', 'MarkerFaceColor','blue','MarkerSize',3);
hold on;
plot(x(dq+1,:),'black','LineWidth',2);
%plot(xhat(dq+1,:),'r','LineWidth',2);
xlabel(texlabel('t'));
ylabel(texlabel('x_1, y'));
hold off;
axis tight
title('(a)')
drawnow

subplot(2,1,2)
plot(x(dq+2,:),'black','LineWidth',2);
hold on
plot(xhat(dq+2,:),'r','LineWidth',2);
plot(x(1,:),'black','LineWidth',2);
for i=1:dq; plot(xhat(i,:),'m','LineWidth',2); end;
for i=1:dq; plot(xhat(i,:)+errors(i,:),'m'); end;
for i=1:dq; plot(xhat(i,:)-errors(i,:),'m'); end;
xlabel(texlabel('t'));
ylabel(texlabel('z, estimated z, x_2, estimated x_2'));
hold off
axis tight
title('(b)')

function r=FitzHughNagumo_int(x,z)
% Function for modeling data, not for UKF execution
a=.7; b=.8; c=3.;
r=[c*(x(2)+x(1)-x(1)^3/3+z); -(x(1)-a+b*x(2))/c];

function r=FitzHughNagumo_obsfct(x)
% Observation function G(x)

    k1=dt*fc(xnl,p);
    k2=dt*fc(xnl+k1/2,p);

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] Voss H U , Timmer J , Kurths J .NONLINEAR DYNAMICAL SYSTEM IDENTIFICATION FROM UNCERTAIN AND INDIRECT MEASUREMENTS[J].International Journal of Bifurcation and Chaos, 2011, 14(6):1905-1905.DOI:10.1142/S0218127404010345.

🌈4 Matlab代码及文献