一、本周周赛总结

• T1 遍历。
• T2 贪心模拟。
• T3 贪心枚举。
• T4 贪心离线+线段树。
  

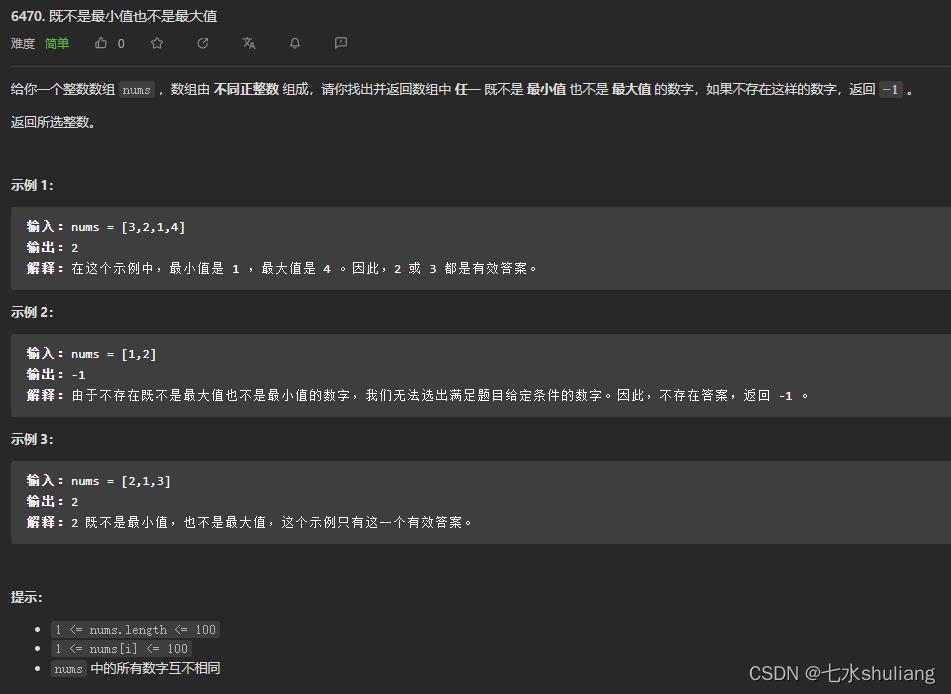
6470. 既不是最小值也不是最大值

6470. 既不是最小值也不是最大值

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def findNonMinOrMax(self, nums: List[int]) -> int:
        mn,mx = min(nums),max(nums)
        for v in nums:
            if mn != v != mx:
                return v
        return -1

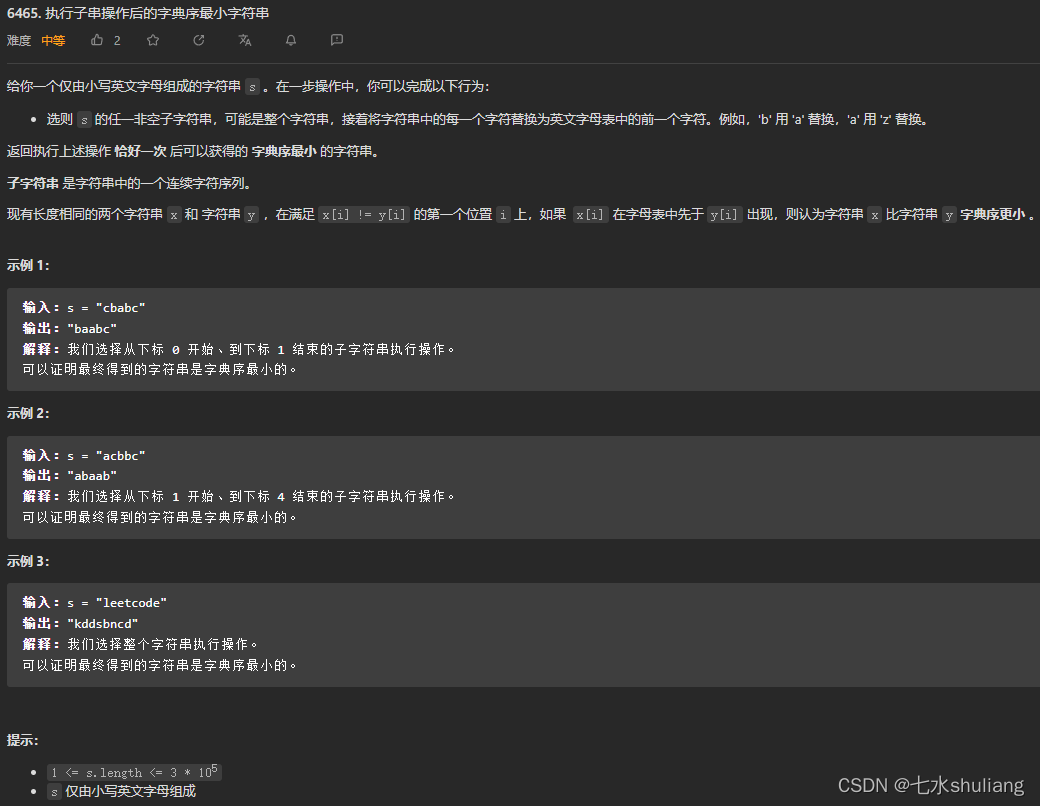
6465. 执行子串操作后的字典序最小字符串

6465. 执行子串操作后的字典序最小字符串

1. 题目描述

2. 思路分析

• 贪心。
• 如果前边是a就跳过，然后找到第一个不是a的位置开始操作，直到遇到a。
• 由于题目要求最少一次，特判全a的数据，把最后一个字符变z。

3. 代码实现

class Solution:
    def smallestString(self, s: str) -> str:
        n = len(s)
        i = 0 
        while i<n and s[i] =='a':
            i += 1
        l = s[:i]
        r = list(s[i:])
        if not r:
            return l[:-1]+'z'
        for i,v in enumerate(r):
            if v == 'a':break 
            r[i] = chr(ord(v)-1)
        return l+''.join(r)

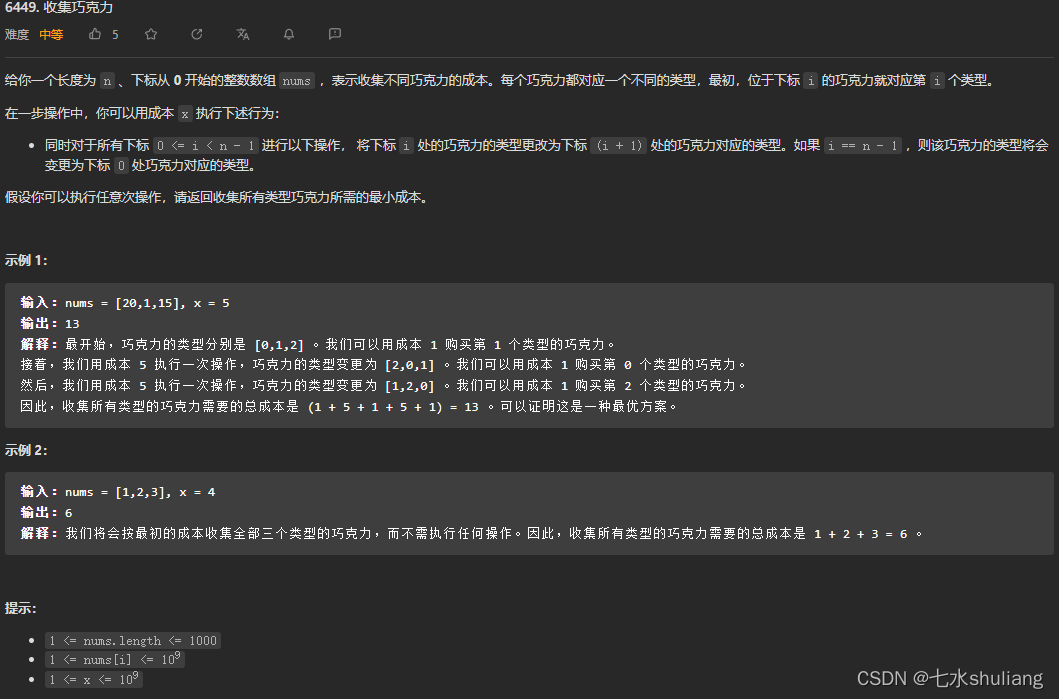
6449. 收集巧克力

6449. 收集巧克力

1. 题目描述

2. 思路分析

• 枚举操作次数，每个位置计算可能的最小值即可。

3. 代码实现

class Solution:
    def minCost(self, nums: List[int], x: int) -> int:
        n = len(nums)
        mn = nums[:]
        ans = sum(nums)
        for i in range(1, n):
            nums = nums[-1:] + nums[:-1]
            for j in range(n):
                mn[j] = min(mn[j], nums[j])
            ans = min(ans, i * x + sum(mn))
        return ans

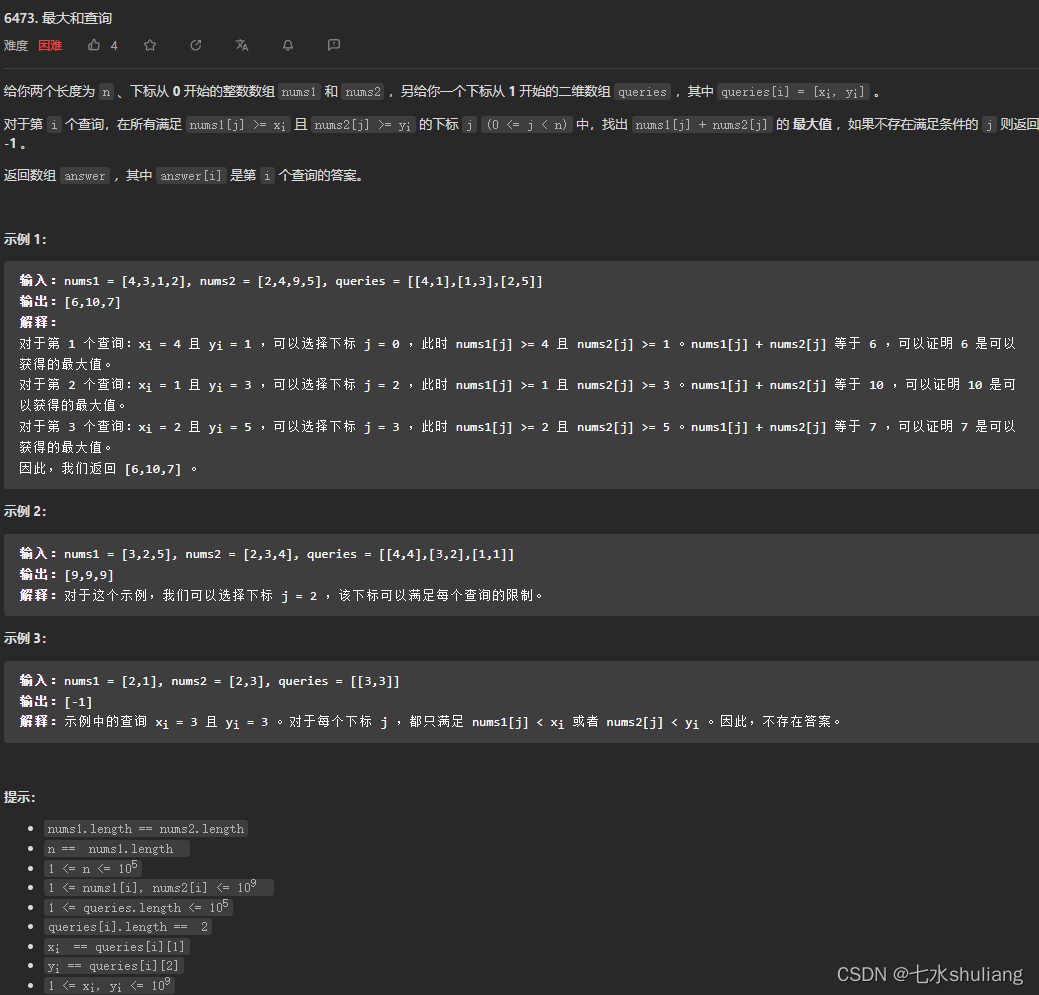
6473. 最大和查询

6473. 最大和查询

1. 题目描述

2. 思路分析

• 一眼出思路离线，由于限制是要最大的，因此降序处理。
• 对于每个query里的x，把所有num1>=x的组合记录，记的数据是(num1,num1+num2)。
• 然后对query里的y找集合里所有超过y的数据对应的最大值，那么可以用线段树处理区间最大值。

---

• 由于y的数据范围很大，需要离散化，数据是query的y和nums2。
• 或者直接用动态开点也可以。
  

3. 代码实现

class ZKW:
    # n = 1
    # size = 1
    # log = 2
    # d = [0]
    # op = None
    # e = 10 ** 15
    """自低向上非递归写法线段树，0_indexed
    tmx = ZKW(pre, max, -2 ** 61)
    """
    __slots__ = ('n', 'op', 'e', 'log', 'size', 'd')

    def __init__(self, V, OP, E):
        """
        V: 原数组
        OP: 操作:max,min,sum
        E: 每个元素默认值
        """
        self.n = len(V)
        self.op = OP
        self.e = E
        self.log = (self.n - 1).bit_length()
        self.size = 1 << self.log
        self.d = [E for i in range(2 * self.size)]
        for i in range(self.n):
            self.d[self.size + i] = V[i]
        for i in range(self.size - 1, 0, -1):
            self.update(i)

    def set(self, p, x):
        # assert 0 <= p and p < self.n
        update = self.update
        p += self.size
        self.d[p] = x
        for i in range(1, self.log + 1):
            update(p >> i)

    def get(self, p):
        # assert 0 <= p and p < self.n
        return self.d[p + self.size]

    def query(self, l, r):  # [l,r)左闭右开
        # assert 0 <= l and l <= r and r <= self.n
        sml, smr, op, d = self.e, self.e, self.op, self.d

        l += self.size
        r += self.size

        while l < r:
            if l & 1:
                sml = op(sml, d[l])
                l += 1
            if r & 1:
                smr = op(d[r - 1], smr)
                r -= 1
            l >>= 1
            r >>= 1
        return self.op(sml, smr)

    def all_query(self):
        return self.d[1]

    def max_right(self, l, f):
        """返回l右侧第一个不满足f的位置"""
        # assert 0 <= l and l <= self.n
        # assert f(self.e)
        if l == self.n:
            return self.n
        l += self.size

        sm, op, d, size = self.e, self.op, self.d, self.size
        while True:
            while l % 2 == 0:
                l >>= 1
            if not (f(op(sm, d[l]))):
                while l < size:
                    l = 2 * l
                    if f(op(sm, d[l])):
                        sm = op(sm, d[l])
                        l += 1
                return l - size
            sm = op(sm, d[l])
            l += 1
            if (l & -l) == l:
                break
        return self.n

    def min_left(self, r, f):
        """返回r左侧连续满足f的最远位置的位置"""
        # assert 0 <= r and r < self.n
        # assert f(self.e)
        if r == 0:
            return 0
        r += self.size
        sm, op, d, size = self.e, self.op, self.d, self.size

        while True:
            r -= 1
            while r > 1 and (r % 2):
                r >>= 1
            if not (f(op(d[r], sm))):
                while r < size:
                    r = (2 * r + 1)
                    if f(op(d[r], sm)):
                        sm = op(d[r], sm)
                        r -= 1
                return r + 1 - size
            sm = op(d[r], sm)
            if (r & -r) == r:
                break
        return 0

    def update(self, k):
        self.d[k] = self.op(self.d[2 * k], self.d[2 * k + 1])

    def __str__(self):
        return str([self.get(i) for i in range(self.n)])

class Solution:
    def maximumSumQueries(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
        n = len(nums1)
        hs = sorted(set(nums2+[y for _,y in queries]))
        size = len(hs)
        a = sorted(zip(nums1,nums2),reverse=True)
        # print(a)
        j = 0
        ans = [-1]*len(queries)
        tree = ZKW([-inf]*size,max,-inf)
        size = max(max(nums2),max(y for _,y in queries))+1
        # print(size)
        for x,y,i in sorted([(x,y,i) for i,(x,y) in enumerate(queries)],reverse=True):
            while j < n and a[j][0] >= x:       
                p = bisect_left(hs,a[j][1])
                tree.set(p,max(a[j][1]+a[j][0],tree.query(p,p+1)))              
                j += 1
            mx = tree.query(bisect_left(hs,y),bisect_left(hs,size+1))
            # print(i,x,y,mx)
            ans[i] = mx if mx > -inf else -1
        return ans                             

参考链接