图论提高
最小生成树
(1)朴素版prim算法( O ( n 2 ) O(n ^ 2) O(n2))
- 适用范围:稠密图
- 易错:注意有向图还是无向图;注意有没有重边和负权边。
- 从一个集合向外一个一个扩展,最开始只有 1 1 1 这个结点,然后把元素一个一个加进来,每次加的元素就是离这个集合距离最小的元素,可以设为 j j j。每次加进来后,就更新其他点到这个集合的距离,更新的数值就是其他点到 j j j 的边的长度。
int g[maxn][maxn], d[maxn], N, M;
bool vis[maxn];
int prim() {
int res = 0;
for (int i = 1; i <= N; i++) d[i] = INF;
for (int i = 0; i < N; i++) {
int t = -1;
for (int j = 1; j <= N; j++) {
if (!vis[j] && (t == -1 || d[t] > d[j])) {
t = j;
}
}
if (i && d[t] == INF) return INF;
if (i) res += d[t];
vis[t] = true;
for (int j = 1; j <= N; j++) d[j] = min(d[j], g[t][j]);
}
return res;
}
(2)堆优化版prim算法( O ( m ∗ l o g n ) O(m * logn) O(m∗logn))
- 适用范围:稀疏图
- 但是这个不怎么用得到。因为稀疏图通常用Kruskal算法,而且这个代码比较长
(2)Kruskal算法
- 适用范围:稀疏图
int N, M, int p[maxn];
struct e{
int u, v, w;
bool operator <(const e& rhe) const{
return w < rhe.w;
}
}edges[maxm];
void init(int N) {
for (int i = 1; i <= N; i++) p[i] = i;
}
int find(int x) {
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void unite(int a, int b) {
if (find(a) == find(b)) return;
p[find(a)] = find(b);
}
int kru() {
init(N);
int cnt = 0, res = 0;
sort(edges, edges + M);
for (int i = 0; i < M; i++) {
auto p = edges[i];
if (find(p.u) != find(p.v)) {
unite(p.u, p.v);
res += p.w;
cnt++;
}
}
if (cnt == N - 1) return res;
return -1;
}
(3)最小生成树的应用
扩展最小生成树:346. 走廊泼水节
- 题意:给定一棵 n ( n ≤ 6000 ) n(n \le 6000) n(n≤6000) 个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。求增加的边的权值总和最小是多少。
- 每次在两个集合之间连边的时候,连的边权是 w i w_i wi,那我们构造完全图的时候,新加的边长是 w i + 1 w_i + 1 wi+1。
- unite那个函数千万别写错!一定要先改变 s z sz sz,再改变 p p p,不然就会出问题!
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 6010;
int p[maxn], sz[maxn], N, M;
void init(int N)
{
for (int i = 1; i <= N; i++)
{
p[i] = i, sz[i] = 1;
}
}
int find(int x)
{
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void unite(int a, int b)
{
if (find(a) == find(b)) return;
sz[find(b)] += sz[find(a)];
p[find(a)] = find(b);
}
struct P
{
int u, v, cost;
bool operator<(const P& rhp)
{
return cost < rhp.cost;
}
}G[maxn];
void solve()
{
init(N);
sort(G, G + M);
int ans = 0;
for (int i = 0; i < M; i++)
{
int u = G[i].u, v = G[i].v, c = G[i].cost;
if (find(u) == find(v)) continue;
ans += (sz[find(u)] * sz[find(v)] - 1) * (c + 1);
unite(u, v);
}
printf("%d\n", ans);
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
scanf("%d", &N);
M = N - 1;
for (int i = 0; i < M; i++)
{
scanf("%d%d%d", &G[i].u, &G[i].v, &G[i].cost);
}
solve();
}
return 0;
}
次小生成树:1148. 秘密的牛奶运输
n ( n ≤ 500 ) n(n \le 500) n(n≤500) 个点, m ( m ≤ 1 0 4 ) m(m \le 10^4) m(m≤104) 条边,边长不超过 1 0 9 10^9 109,问次小生成树的值是多少.
- 次小生成树:把一个带权的图,把图的所有生成树按权值从小到大排序,第二小的成为次小生成树。严格次小生成树是边权和严格大一点,非严格次小生成树是指边权和可以相等。
- 法一(只能求非严格的次小生成树):先求最小生成树,再枚举删去最小生成树中的边求解。时间复杂度。 O ( m l o g m + n m ) O(mlogm + nm) O(mlogm+nm)
- 法二:先求最小生成树(严格与非严格的都可以求),然后依次枚举非树边,然后将该边加入树中,同时从树中去掉一条边, 使得最终的图仍是一棵树。则一定可以求出次小生成树。 O ( m + n 2 + m l o g m ) O(m + n^2 + mlogm) O(m+n2+mlogm)。
- 法二的原理:设T为图G的一棵生成树,对于非树边a和树边b,插入边a,并删除边b的操作记为 ( + a , − b ) (+a, -b) (+a,−b)。如果T+a-b之后,仍然是一棵生成树,称 ( + a , − b ) (+a,-b) (+a,−b) 是 T T T 的一个可行交换。称由 T T T 进行一次可行变换所得到的新的生成树集合称为 T T T 的邻集。定理:(严格与非严格)次小生成树一定在最小生成树的邻集中。
- 步骤:
- 求最小生成树,统计标记每条边是树边,还是非树边;同时把最小生成树建立出来。
- 预处理任意两点间的边权最大值 d 1 [ a ] [ b ] d1[a][b] d1[a][b]与次大值 d 2 [ a ] [ b ] d2[a][b] d2[a][b]。
- 依次枚举所有非树边,求
m
i
n
(
s
u
m
+
w
−
d
1
[
a
]
[
b
]
)
min(sum +w - d1[a][b])
min(sum+w−d1[a][b]), 满足
w
>
d
2
[
a
]
[
b
]
w > d2[a][b]
w>d2[a][b],其中
d
i
s
t
[
a
]
[
b
]
dist[a][b]
dist[a][b]是节点a和节点b的在树上的所经路径最大边的边权,w是非树边。若
w
=
=
d
2
[
a
]
[
b
]
w == d2[a][b]
w==d2[a][b],则去处理次大边。
(注:如果加上的边和两点之间最大边长度相等,那么只能求非严格次小生成树。若要求严格次小生成树,还要在上述情况出现的情况下,改为去掉次大边)。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 510, maxm = 10010;
typedef long long ll;
int h[maxn], ne[maxn * 2], e[maxn * 2], w[maxn * 2], idx;
int N, M, p[maxn], d1[maxn][maxn], d2[maxn][maxn];
ll sum;
struct P {
int u, v, c;
bool f;
bool operator<(const P& rhp)const {
return c < rhp.c;
}
}G[maxm];
void init(int N) {
for (int i = 1; i <= N; i++) p[i] = i;
}
int find(int x) {
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void unite(int a, int b) {
if (find(a) == find(b)) return;
p[find(a)] = find(b);
}
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void mst() {
init(N);
sort(G, G + M);
for (int i = 0; i < M; i++) {
int u = G[i].u, v = G[i].v, c = G[i].c;
if (find(u) == find(v)) continue;
unite(u, v);
G[i].f = 1;
sum += c;
add(u, v, c), add(v, u, c);
}
}
void dfs(int u, int fa, int max1, int max2, int d1[], int d2[]) {
//一旦出现最大值,就把最大值变成次大值。
d1[u] = max1, d2[u] = max2;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v != fa) {
int t1 = max1, t2 = max2;
if (w[i] > max1) t2 = max1, t1 = w[i];
else if (w[i] < max1 && w[i] > max2) t2 = w[i];
dfs(v, u, t1, t2, d1, d2);
}
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &N, &M);
for (int i = 0; i < M; i++) {
scanf("%d%d%d", &G[i].u, &G[i].v, &G[i].c);
}
mst();
for (int i = 1; i <= N; i++) dfs(i, -1, 0, 0, d1[i], d2[i]);
ll ans = 1e18;
for (int i = 0; i < M; i++) {
int u = G[i].u, v = G[i].v, c = G[i].c;
//printf("### %d %d %d %d %d %d\n", u, v, c, G[i].f, d1[u][v], d2[u][v]);
if (!G[i].f) {
if(c > d1[u][v]) ans = min(ans, sum + c - d1[u][v]);
else if (c == d1[u][v] && c > d2[u][v]) ans = min(ans, sum + c - d2[u][v]);
}
}
printf("%lld\n", ans);
return 0;
}
二分图
概念
- 一个图是二分图,等价于图不含有奇数环(环的边数是奇数),也等价于染色的过程一定是没有矛盾。
- 二分图:就是顶点集 V V V 可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
- 二分图的匹配:给定一个二分图 G G G,在 G G G 的一个子图M中, M M M 的边集 { E } \{E\} {E} 中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
- 二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
- 匹配点:二分图匹配中,被匹配的点。
- 增广路径:若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
- 最大匹配等价于不存在增广路径。
- 在二分图中,最大匹配数 = 最小点覆盖 = 总点数 - 最大独立集 = 总点数 - 最小路径覆盖
- 点覆盖,对于图G=(V,E),选出一个点集S⊆V,使得E中每一条边至少有一个端点在S中。而最小点覆盖是点集最小的情况。在二分图中,最大匹配数 = 最小点覆盖。
- 最大独立集:选出最多的点,使得选出的点之间没有边。
- 最大团:选出最多的点,使得选出的点之间都有边。
- 原图的最大独立集就是补图的最大团。
- 在二分图中求最大独立集 ( n − m ) (n - m) (n−m) ⇔ \Leftrightarrow ⇔ 去掉最少的点,将这些点拿去之后,图中所有的边都会去掉 ( m ) (m) (m) ⇔ \Leftrightarrow ⇔ 找到最小点覆盖 ( m ) (m) (m) ⇔ \Leftrightarrow ⇔ 找到最大匹配 ( m ) (m) (m).
- 最小不相交路径覆盖(最小路径点覆盖):给一个有向图 G = ( V , E ) G=(V, E) G=(V,E),找一些没有任何重复点的路径,使得这些路径经过了每一个点。注意路径的长度可以是 0 0 0,即只包含一个节点。
- 我们关心的时求 D A G DAG DAG 的最小路径点覆盖。
- 拆点:把每个点拆成入点和出点两个,原图中每一条 i → j i \rightarrow j i→j,都变成 i → j ′ i \rightarrow j' i→j′。新图就变成二分图了(左部的点是入点,右部的点是出点)。
- 每一条路径终点与左侧非匹配点一一对应。我们的目的是让左侧非匹配点最少 ( n − m ) (n - m) (n−m),等价于让左侧匹配点最多(m),那么就是最大匹配 ( m ) (m) (m)。
- 最小可相交路径覆盖(最小路径重复点覆盖):与上面的有点不同的是,这个问题的不同路径可以包含相同的点和边,
- 这种问题,可以先求出传递闭包 G ′ G' G′,然后再 G ′ G' G′ 上求最小不相交路径覆盖。
(1)染色法(dfs)(O(m + n))
- 注意啊,二分图的重要性是在概念与性质,染色只是判定方法。
- 易错:h别忘初始化,以及初始化的位置一定要在输入边之前。另外一定把color涂成1或-1,别涂成0或1,否则不能区分有哪些点还没涂。
int N, M, color[maxn];
int h[maxn], e[maxm], ne[maxm], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c) {
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!color[v] && !dfs(v, -c)) return false;
else if (color[v] == c) return false;
}
return true;
}
void check() {
for (int i = 1; i <= N; i++) {
if (!color[i]) {
if (!dfs(i, 1)) {
printf("No\n");
return;
}
}
}
printf("Yes\n");
}
257. 关押罪犯
- 题意:有 n n n 个罪犯,某些罪犯之间有怨气 c c c(关在同一监狱会产生规模大小 c c c 的冲突),现在要把罪犯分开关到两个监狱中,通过合理分配,问他们产生冲突最大值 最小是多少?
法一
- 我们希望把冲突值不大于x的可以关在一个房间里,把大于x的必须关在两个房间里。因此,就是边权不大于x的可以在二分图的一侧,但是大于x的两个顶点必须属于二分图的两侧。因此图中只需要保留不大于x的边就行。
- 新图中没有边代表关在两个监狱之中,没有边的话会冲突,那么关在同一监狱之中。我们希望冲突都是小于 a n s ans ans 的,那么大于 a n s ans ans 时都认为没有冲突,那么大于 a n s ans ans 的边的两个顶点必须在两个监狱之中。那么,问题变成了,把所有大于 a n s ans ans 的边全部筛选出来,看看这个新图能否分成两部分。
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 20010, maxm = 200010;
int h[maxn], e[maxm], ne[maxm], w[maxm], idx;
int N, M, color[maxn];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
bool dfs(int u, int c, int x) {
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) {
if (w[i] <= x) continue;
int v = e[i];
//小心这里的!dfs(v, -c, x), 千万别写错!
if (!color[v] && !dfs(v, -c, x)) return false;
else if (color[v] == c) return false;
}
return true;
}
bool C(int x) {
memset(color, 0, sizeof color);
for (int i = 1; i <= N; i++) {
if (!color[i]) {
if (!dfs(i, 1, x)) return false;
}
}
return true;
}
int main() {
scanf("%d%d", &N, &M);
memset(h, -1, sizeof h);
for (int i = 0; i < M; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
int lb = -1, ub = 1e9 + 1;
while (ub - lb > 1) {
int mid = (lb + ub) / 2;
if (C(mid)) ub = mid;
else lb = mid;
}
printf("%d\n", ub);
return 0;
}
法二
-
贪心+二分、并查集
-
这个还是依附于二分图。我们从大到小把边的权值进行排序。然后,由于我们尽可能让矛盾大的两个罪犯关到不同的监狱里,因此,把边的权值从大到小遍历,并分别加到二分图的两个不同的位置。一旦发现冲突的时候,就说明可以输出答案了。
-
可以画一个只有 1 , 2 , 3 1,2,3 1,2,3 的例子, 1 1 1 和 2 2 2 冲突, 2 2 2 和 3 3 3 冲突, 1 1 1 和 3 3 3 冲突,那么我们只能保证其中的两个不会发生冲突,那么第三个冲突发生的时候,我们会发现他们两个的虚点已经在同一个并查集中了.
-
这样,我们利用虚点就可以判断了。注意处理边界!如N == 1的时候。
-
什么是虚点?虚点怎么用?AcWing 257题解
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxm = 100010;
int p[40010];
void init(int N) {
for (int i = 1; i <= N; i++) p[i] = i;
}
int find(int x) {
if (x == p[x]) return x;
return p[x] = find(p[x]);
}
void unite(int x, int y) {
if (find(x) == find(y)) return;
p[find(x)] = find(y);
}
struct e {
int u, v, w;
bool operator < (const e& rhe)const {
return w > rhe.w;
}
}G[maxm];
int main() {
int N, M;
scanf("%d%d", &N, &M);
for (int i = 0; i < M; i++) {
scanf("%d%d%d", &G[i].u, &G[i].v, &G[i].w);
}
sort(G, G + M);
init(2 * N);
for (int i = 0; i < M; i++) {
int px = find(G[i].u), py = find(G[i].v);
if (px == py) {
printf("%d\n", G[i].w);
return 0;
}
p[px] = find(G[i].v + N);
p[py] = find(G[i].u + N);
}
printf("%d\n", 0);
return 0;
}
(2)匈牙利算法O(mn)
必须要指出,匈牙利算法建立的都是单向边!
861. 二分图的最大匹配
-
给定一个二分图,其中左半部包含 n 1 n1 n1 个点(编号 1 ∼ n 1 1∼n_1 1∼n1),右半部包含 n 2 n_2 n2 个点(编号 1 ∼ n 2 1∼n_2 1∼n2),二分图共包含 m m m 条边。数据保证任意一条边的两个端点都不可能在同一部分中。请你求出二分图的最大匹配数。
-
一般运行时间都远小于 O ( m n ) O(mn) O(mn)。
-
这个算法就是求二分图的最大匹配数,即匹配的边数。尽管 d f s dfs dfs 是从顶点出发,但是最后的 a n s ans ans 就是最大匹配的边数。
-
有一个需要强调一下,尽管二分图是无向图问题,但是我们处理的时候都是将一条无向边转化为一条有向边。
-
一定要小心,这个算法的节点编号是从1开始的,如果从0开始,就得把match数组初始化为-1,在改动一下相关部分
int h[maxn], e[maxm], ne[maxm], idx;
int N1, N2, M, match[maxn];
bool vis[maxn];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u) {
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!vis[v]) {
vis[v] = true;
//小心这个地方是find(match[v]), 极易错!
if (match[v] == 0 || find(match[v])) {
match[v] = u;
return true;
}
}
}
return false;
}
int main() {
scanf("%d%d%d", &N1, &N2, &M);
memset(h, -1, sizeof h);
while(M--) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
int ans = 0;
for (int i = 1; i <= N1; i++) {
memset(vis, false, sizeof vis);
if (find(i)) ans++;
}
printf("%d\n", ans);
return 0;
}
372. 棋盘覆盖
-
给定一个 N 行 N 列的棋盘,已知某些格子禁止放置。求最多能往棋盘上放多少块的长度为 2、宽度为 1 的骨牌,骨牌的边界与格线重合(骨牌占用两个格子),并且任意两张骨牌都不重叠。
-
i + j i + j i+j 是奇数时与 i + j i + j i+j 是偶数时的格子是两两相邻的。而奇偶性相同时是不相邻的。这就是一个二分图。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 110;
typedef pair<int, int> P;
P match[maxn][maxn];
int N, M;
bool vis[maxn][maxn], g[maxn][maxn];
int dx[] = { 1, -1, 0, 0 }, dy[] = { 0, 0, 1, -1 };
bool find(int x, int y) {
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < 1 || nx > N || ny < 1 || ny > N) continue;
if (vis[nx][ny] || g[nx][ny]) continue;
vis[nx][ny] = true;
P t = match[nx][ny];
if (!t.first || find(t.first, t.second)) {
//小心!make_pair(x, y)别写错!
match[nx][ny] = make_pair(x, y);
return true;
}
}
return false;
}
int main() {
scanf("%d%d", &N, &M);
while (M--) {
int a, b;
scanf("%d%d", &a, &b);
g[a][b] = true;
}
int ans = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if ((i + j) % 2 && !g[i][j]) {
memset(vis, 0, sizeof vis);
if (find(i, j)) ans++;
}
}
}
printf("%d\n", ans);
return 0;
}
(3)二分图最小点覆盖
- 最小点覆盖 = 最大匹配数
- 其实要注意到,二分图的匹配,匹配点的数量是匹配边数量的两倍。因为每个匹配点有且仅有一条匹配的边与之相连。
- 最小点覆盖可以这样构造:求最大匹配;从左部的每个非匹配点出发,做一遍增广路径,标记所有经过的点;选出左部所有未被标记的点,右部所有被标记的点。
- 原理:左部所有非匹配的点,一定被标记;右边所有非匹配的点,一定不被标记。对于每个匹配边,要么两个端点同时被标记,要么同时不被标记;对于所有非匹配边,两种情况:(1)左边非匹配点 -> 右边匹配点,此时右边一定会被标记,因此会被选出;(2)左边匹配点 -> 右边非匹配点,左边的一定不被标记,仍然可以选出。
376. 机器任务
-
有两台机器 A , B A,B A,B 以及 K K K 个任务。机器 A A A 有 N 种不同的模式(模式 0 ∼ N − 1 0∼N−1 0∼N−1),机器 B B B 有 M M M 种不同的模式(模式 0 ∼ M − 1 0∼M−1 0∼M−1)。两台机器最开始都处于模式 0。每个任务既可以在 A A A 上执行,也可以在 B B B 上执行。对于每个任务 i i i,给定两个整数 a [ i ] a[i] a[i] 和 b [ i ] b[i] b[i],表示如果该任务在 A A A 上执行,需要设置模式为 a [ i ] a[i] a[i],如果在 B B B 上执行,需要模式为 b [ i ] b[i] b[i]。任务可以以任意顺序被执行,但每台机器转换一次模式就要重启一次。求怎样分配任务并合理安排顺序,能使机器重启次数最少。
-
仔细分析,这个类似最小点覆盖的问题。但是有两点需要注意:
- 编号是从 0 0 0 开始的, m a t c h match match 要初始化为 − 1 -1 −1
- a a a 或 b b b 的编号为 0 0 0 时不用考虑,因为 0 0 0 时不用转换机器。这个要是忽略掉的话,结果有可能会比答案多 1 1 1
#include<bits/stdc++.h>
using namespace std;
const int maxn = 110, maxm = 2010;
int h[maxn], e[maxm], ne[maxm], idx;
int N1, N2, M, match[maxn];
bool vis[maxn];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u) {
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!vis[v]) {
vis[v] = true;
if (match[v] == -1 || find(match[v])) {
match[v] = u;
return true;
}
}
}
return false;
}
int main() {
while (scanf("%d", &N1) && N1) {
memset(h, -1, sizeof h);
memset(match, -1, sizeof match);
idx = 0;
scanf("%d%d", &N2, &M);
for (int i = 0; i < M; i++) {
int id, a, b;
scanf("%d%d%d", &id, &a, &b);
//0的时候不用转换状态。
if (a == 0 || b == 0) continue;
add(a, b);
}
int ans = 0;
for (int i = 1; i < N1; i++) {
memset(vis, 0, sizeof vis);
if (find(i)) ans++;
}
printf("%d\n", ans);
}
return 0;
}
(4)二分图最大独立集
378. 骑士放置
-
给定一个 N×M 的棋盘,有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的骑士(国际象棋的“骑士”,类似于中国象棋的“马”,按照“日”字攻击,但没有中国象棋“别马腿”的规则)。
-
在一个N * M的棋盘上,可以放多少个国际象棋中的骑士。

-
由此可以看出,骑士每跳一次,格子的奇偶性就会改变。这个问题就等价于,能选出多少个格子,使得两两之间没有边。最终答案就是:N * M - k - 最大匹配数量
-
一般的图中求最大独立集是一个 NP-Hard 问题,只有二分图才可以用匈牙利算法。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 110;
typedef pair<int, int> P;
P match[maxn][maxn];
bool g[maxn][maxn], vis[maxn][maxn];
int N, M, K;
int dx[] = { -1, -2, -2, -1, 1, 2, 2, 1 }, dy[] = { -2, -1, 1, 2, 2, 1, -1, -2 };
bool find(int x, int y) {
for (int i = 0; i < 8; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < 1 || nx > N || ny < 1 || ny > M) continue;
if (vis[nx][ny] || g[nx][ny]) continue;
vis[nx][ny] = true;
P t = match[nx][ny];
if (t.first == 0 || find(t.first, t.second)) {
match[nx][ny] = { x, y };
return true;
}
}
return false;
}
int main() {
scanf("%d%d%d", &N, &M, &K);
for(int i = 0; i < K; i++) {
int x, y;
scanf("%d%d", &x, &y);
g[x][y] = true;
}
int res = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
//这个地方写成 (i + j) % 2 == 1 也是可以过的。
if ((i + j) % 2 || g[i][j]) continue;
memset(vis, 0, sizeof vis);
if (find(i, j)) res++;
}
}
printf("%d\n", N * M - K - res);
return 0;
}
(5)有向无环图的最小路径点覆盖
379. 捉迷藏
- 题意:求一个 D A G DAG DAG 中最多可以挑出多少个点,使得这些点两两不可达。
- 有向无环图本身就是二分图,而且图都给你搭建好了,无需再考虑怎么把点集分成两个集合然后连边了(那个是建图的时候才需要考虑的问题),跑一遍传递闭包算法然后就可以直接匹配了。
- 答案就是这个图的最小路径重复点覆盖为 m m m,则答案就是 N − m N-m N−m.
#include<bits/stdc++.h>
using namespace std;
const int maxn = 210;
bool d[maxn][maxn], vis[maxn];
int N, M, match[maxn];
void Floyd_Warshall() {
for (int k = 1; k <= N; k++) {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) d[i][j] |= d[i][k] & d[k][j];
}
}
}
bool find(int u) {
for (int i = 1; i <= N; i++) {
if (d[u][i] && !vis[i]) {
vis[i] = true;
//一开始又双叒叕把 find(match[i]) 写错了!看清楚!
if (!match[i] || find(match[i])) {
match[i] = u;
return true;
}
}
}
return false;
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 0; i < M; i++) {
int a, b;
scanf("%d%d", &a, &b);
d[a][b] = true;
}
Floyd_Warshall();
int res = 0;
for (int i = 1; i <= N; i++) {
memset(vis, 0, sizeof vis);
if (find(i)) res++;
}
printf("%d\n", N - res);
return 0;
}
差分约束
- 对于最短路问题,那么图中有一条从 u u u 到 v v v 的边,等价于不等式 d i s v ≤ d i s u + w ( u , v ) dis_v \le dis_u + w(u,v) disv≤disu+w(u,v). 因此一个最短路问题等价于一大堆 ≤ \le ≤ 不等式,而最短路的话,就是一个最小的上界。
- 对于最长路问题,那么图中有一条从 u u u 到 v v v 的边,等价于不等式 d i s v ≥ d i s u + w ( u , v ) dis_v \ge dis_u + w(u,v) disv≥disu+w(u,v). 因此一个最长路问题等价于一大堆 ≥ \ge ≥ 不等式,而最长路的话,就是一个最大的下界。
步骤
求不等式组的可行解
- 源点需要满足的条件:从源点出发,一定可以走到所有的边.
- 步骤:
- 先将每个不等式 x i ≤ x j + c k x_i \le x_j + c_k xi≤xj+ck,转化成一条 x j x_j xj 走到 x i x_i xi,长度为 c k c_k ck 的一条边。注意一定要转化为不等关系。
- 找一个超级源点,使得该源点一定可以遍历到所有边。
- 从源点求一遍单源最短路:如果存在负环,则原不等式组一定无解;如果没有负环,则
d
i
s
t
[
i
]
dist[i]
dist[i] 就是原不等式组的一个可行解。
注:如果是转化为最长路问题的话,那么就是寻找是否存在正环。存在正环就是无解。
**解释:如果是求最大值,那么我们有一系列 x n ≤ x 0 + ∑ a i c i x_n \le x_0 + \sum\limits a_ic_i xn≤x0+∑aici 不等式,那么要满足所有不等式的话,就要满足最小上界,因此是求最小值,即求最短路. **
-
如何求最大值或者最小值(最大的可行解或是最小的可行解):
-
结论:如果是求最小值,则应该求最长路;如果是求最大值,则应该求最短路。
-
问题:如何转化 x i ≤ C x_i \le C xi≤C,其中 c c c 是一个常数,这类的不等式
-
方法:建立一个超级源点, 0,然后建立 0 → i 0 \rightarrow i 0→i, 长度是 c c c 的边即可。
-
以求 x i x_i xi 的最大值为例:求所有从 x i x_i xi 出发,构成的不等式链 x i ≤ x j + c 1 ≤ x k + c 2 + c 1 ≤ . . . ≤ c 1 + c 2 + . . . + c k x_i \le x_j+ c_1 \le x_k+c_2+c_1 \le... \le c_1+c_2+... + c_k xi≤xj+c1≤xk+c2+c1≤...≤c1+c2+...+ck
所计算出的上界,最终 x i x_i xi 的最大值等于所有上界的最小值。 -
还是要强调一下,求负环的话还是要优先选择朴素的方法,用队列与cnt数组来实现。不过TLE的话还是改成栈吧。
-
总之:最小值问题,转化为一系列大于等于不等式,并求最长路;最大值问题,转化为一系列小于等于不等式,并求最短路。
1.1170. 排队布局
对
n
(
n
≤
1000
)
n(n \le 1000)
n(n≤1000) 个点摆放位置(这些点要按照编号在数轴上排成一队),但是点与点之间的距离需要满足一定的条件:
M
L
(
1
≤
M
L
≤
10
,
000
)
ML(1 \le ML \le 10,000)
ML(1≤ML≤10,000) 描述了某两个点之间的距离不能超过多少;
M
D
(
1
≤
M
D
≤
10
,
000
)
MD(1 \le MD \le 10,000)
MD(1≤MD≤10,000) 描述了某两个点之间的距离不能少于多少。计算
1
1
1 号点和
n
n
n 号点的最大距离.输出一个整数,如果不存在满足要求的方案,输出-1;如果 1 号奶牛和 N 号奶牛间的距离可以任意大,输出-2;
x
0
≤
x
i
−
1
x
j
≤
x
i
+
c
(
i
<
j
)
x
i
≤
x
j
−
c
(
i
<
j
)
x
i
−
1
≤
x
i
x_0 \le x_i - 1 \\ x_j \le x_i + c \quad (i < j) \\ x_i \le x_j - c \quad (i < j) \\ x_{i-1} \le x_i
x0≤xi−1xj≤xi+c(i<j)xi≤xj−c(i<j)xi−1≤xi
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1010, maxm = 21010;
const ll INF = 1e18;
int h[maxn], e[maxm], ne[maxm], w[maxm], idx;
int N, M1, M2, cnt[maxn];
ll d[maxn];
bool vis[maxn];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
ll spfa() {
queue<int> que;
fill(d, d + maxn, INF);
d[1] = 0;
for (int i = 1; i <= N; i++)
{
vis[i] = true;
que.push(i);
}
while (que.size())
{
int u = que.front(); que.pop();
vis[u] = false;
for (int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if (d[v] > d[u] + w[i]) {
d[v] = d[u] + w[i];
cnt[v] = cnt[u] + 1;
if (cnt[v] >= N) return -1;
if (!vis[v]) {
vis[v] = true;
que.push(v);
}
}
}
}
if (d[N] >= INF / 2) return -2;
return d[N];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d%d", &N, &M1, &M2);
for (int i = 0; i < M1; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
if (a > b) swap(a, b);
add(a, b, c);
}
for (int i = 0; i < M2; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
if (a > b) swap(a, b);
add(b, a, -c);
}
for (int i = 2; i <= N; i++) {
add(i, i - 1, 0);
}
ll ans = spfa();
printf("%lld\n", ans);
return 0;
}
1169. 糖果

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<stack>
using namespace std;
typedef long long ll;
//这个maxm必须开到300010,因为x=1时会加双向边,而且每一个节点与0都要连一条边。
const int maxn = 100010, maxm = 300010;
const ll INF = 1e16;
int h[maxn], e[maxm], ne[maxm], w[maxm], idx;
int N, M, cnt[maxn];
bool vis[maxn];
ll d[maxn];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
bool spfa() {
stack<int> s;
fill(d, d + maxn, -INF);
//当时spfa求负环把所有点都加到队列里面的一个重要原因是图可能是不连通的。
//但是这个图从0节点一定可以遍历完所有节点,因此只把0节点加入栈中就可以。
d[0] = 0, s.push(0), vis[0] = true;
while (s.size()) {
int u = s.top(); s.pop();
vis[u] = false;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (d[v] < d[u] + w[i]) {
d[v] = d[u] + w[i];
cnt[v] = cnt[u] + 1;
//注意,因为加上0号节点了,所以是N + 1个点。
if (cnt[v] >= N + 1) return true;
if (!vis[v]) {
s.push(v);
vis[v] = true;
}
}
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; i++) add(0, i, 1);
for (int i = 0; i < M; i++) {
int x, a, b;
scanf("%d%d%d", &x, &a, &b);
if (x == 1) add(a, b, 0), add(b, a, 0);
else if (x == 2) add(a, b, 1);
else if (x == 3) add(b, a, 0);
else if (x == 4) add(b, a, 1);
else if (x == 5) add(a, b, 0);
}
if (spfa()) printf("-1\n");
else {
ll ans = 0;
for (int i = 1; i <= N; i++) ans += d[i];
printf("%lld\n", ans);
}
return 0;
}
最近公共祖先
在线求LCA:1172. 祖孙询问
- 题意:给两个点,询问两个点是否一个是另一个的祖先。
- 倍增法:
- f a [ i , j ] fa[i, j] fa[i,j] 表示从 i i i 开始,向上走 2 j 2^j 2j 能走到的节点 ( 0 ≤ j ≤ log n ) (0 \le j \le \log n) (0≤j≤logn); d e p t h [ i ] depth[i] depth[i] 表示 i i i 的深度。
- 哨兵:从 i i i 开始跳 2 j 2^j 2j 会跳过根节点,则定义 f [ i , j ] = 0 f[i, j] = 0 f[i,j]=0, 且 d e p t h [ 0 ] = 0 depth[0] = 0 depth[0]=0.
- 步骤:先将两个点跳到同一层。若两个点不是同一点让两个点同时往上跳,知道跳到最近公共祖先的下一层(即最近公共祖先的儿子)。
- 预处理: O ( n ∗ l o g n ) O(n*logn) O(n∗logn);查询: O ( l o g n ) O(logn) O(logn)
- f a [ n ] [ k ] fa[n][k] fa[n][k] 第二维数组大小: l o g 2 ( m a x n ) log_2(maxn) log2(maxn) 向下取整,比如 l o g 2 ( 100000 ) = 16 log_2(100000)=16 log2(100000)=16,所以 k 取值是 0~16,所以第二维开17即可。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int maxn = 40010, maxm = maxn * 2;
int h[maxn], ne[maxm], e[maxm], idx;
int N, M, root;
int depth[maxn], fa[maxn][16];
void bfs() {
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[root] = 1;
queue<int> que;
que.push(root);
while (que.size()) {
int u = que.front(); que.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (depth[v] > depth[u] + 1) {
depth[v] = depth[u] + 1;
que.push(v);
fa[v][0] = u;
for (int k = 1; k <= 15; k++) fa[v][k] = fa[fa[v][k - 1]][k - 1];
}
}
}
}
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
//二次方拼凑一定要倒着拼凑。
for (int k = 15; k >= 0; k--) {
if (depth[fa[a][k]] >= depth[b]) a = fa[a][k];
}
if (a == b) return a;
for (int k = 15; k >= 0; k--) {
if (fa[a][k] != fa[b][k]) {
a = fa[a][k];
b = fa[b][k];
}
}
//返回a的节点,即a的公共祖先。
return fa[a][0];
}
int main() {
scanf("%d", &N);
memset(h, -1, sizeof h);
for (int i = 0; i < N; i++) {
int a, b;
scanf("%d%d", &a, &b);
if (b == -1) root = a;
else add(a, b), add(b, a);
}
bfs();
scanf("%d", &M);
while (M--) {
int a, b;
scanf("%d%d", &a, &b);
int p = lca(a, b);
if (p == a) printf("1\n");
else if (p == b) printf("2\n");
else printf("0\n");
}
return 0;
}
离线求LCA:1171. 距离
- 题意:多次询问树上两点之间的距离(树上两个节点的距离是唯一的)。边是无向的,节点的编号是从 1 ∼ n 1 \sim n 1∼n.
- 在线做法:读入一个询问,输出一个结果。离线做法:读入所有询问,统一输出结果。
- T a r j a n Tarjan Tarjan——离线LCA: O ( n + m ) O(n + m) O(n+m)
- 这个算法的思想是:
- 在深度优先搜索的过程中,把所有节点分为三大类:已经遍历过,且回溯过的点(标记为2);正在搜索的分支(标记为1);还未搜索到的点(标记为0)。
- 保存下来所有询问,每次询问的时候,一定是一个结点是第2类,一个结点是第1类
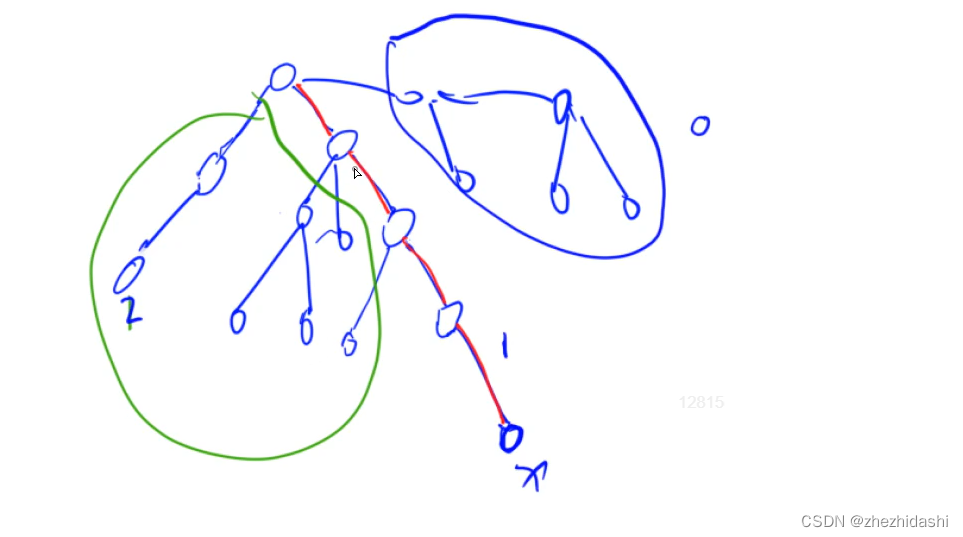
- 正在搜索的节点 u u u,与询问相关 v v v,最近公共祖先记为 p [ v ] p[v] p[v],距离就是 d [ u ] + d [ v ] − d [ p [ v ] ] ∗ 2 d[u] + d[v] - d[p[v]] * 2 d[u]+d[v]−d[p[v]]∗2
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
typedef pair<int, int> P;
const int maxn = 10010, maxm = maxn * 2;
int h[maxn], ne[maxm], e[maxm], w[maxm], idx;
int st[maxn], N, M, p[maxn], ans[maxm], d[maxn];
vector<P> query[maxn];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void dfs(int u, int fa) {
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v == fa) continue;
d[v] = d[u] + w[i];
dfs(v, u);
}
}
void init(int N){
for(int i = 1; i <= N; i++) p[i] = i;
}
int find(int x) {
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void tarjan(int u) {
st[u] = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!st[v]) {
tarjan(v);
//只有状态为 2 的点往上走,走到第一个状态为 1 的点才可以算作并查集中的 parent。因此只有这个点完全变成状态为2的点的时候,才可以让 p[v] 变为 u.
p[v] = u;
}
}
for (auto p : query[u]) {
int v = p.first, id = p.second;
if (st[v] == 2) {
int anc = find(v);
ans[id] = d[u] + d[v] - 2 * d[anc];
}
}
st[u] = 2;
}
int main() {
scanf("%d%d", &N, &M);
memset(h, -1, sizeof h);
for (int i = 1; i < N; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for (int i = 0; i < M; i++) {
int a, b;
scanf("%d%d", &a, &b);
if (a != b) {
query[a].push_back({ b, i });
query[b].push_back({ a, i });
}
}
init(N);
dfs(1, -1);
tarjan(1);
for (int i = 0; i < M; i++) printf("%d\n", ans[i]);
return 0;
}
356. 次小生成树
-
给定一张 N N N 个点 M M M 条边的无向图,求无向图的严格次小生成树。设最小生成树的边权之和为 s u m sum sum,严格次小生成树就是指边权之和大于 s u m sum sum 的生成树中最小的一个。 N ≤ 1 0 5 , M ≤ 3 × 1 0 5 N≤10^5,M≤3×10^5 N≤105,M≤3×105
-
f a ( i , j ) fa(i, j) fa(i,j):从 i i i 开始,往上跳 2 j 2^j 2j 步是哪个节点。
-
d 1 ( i , j ) d_1(i, j) d1(i,j):从 i i i 开始,往上跳 2 j 2^j 2j 步,这些 2 j 2^j 2j 边中边权最大值。
-
d 2 ( i , j ) d_2(i, j) d2(i,j):从 i i i 开始,往上跳 2 j 2^j 2j 步,这些 2 j 2^j 2j 边中边权次大值。
-
思路:
- 先构建出最小生成树,标注每条边是否是当前最小生成树的边.
- 然后剩余的每一条边尝试往上加,然后在形成的环中对应最小生成树中的边中删掉最大边;若最大边和新加进来的边相同,就加上次大边.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100010, maxm = 300010, INF = 0x3f3f3f3f;
int h[maxn], e[maxm], ne[maxm], w[maxm], idx;
int p[maxn], N, M;
int d1[maxn][17], d2[maxn][17], fa[maxn][17], depth[maxn];
ll sum;
struct edge {
int u, v, w;
bool used;
bool operator<(const edge& rhe)const
{
return w < rhe.w;
}
}G[maxm];
void init(int N)
{
for (int i = 1; i <= N; i++) p[i] = i;
}
int find(int x) {
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void unite(int a, int b) {
if (find(a) == find(b)) return;
p[find(a)] = find(b);
}
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void kruskal() {
init(N);
sort(G, G + M);
for (int i = 0; i < M; i++) {
int u = G[i].u, v = G[i].v, w = G[i].w;
if (find(u) != find(v)) {
unite(u, v);
G[i].used = true;
sum += w;
}
}
}
//建出最小生成树构成的数。
void build() {
memset(h, -1, sizeof h);
for (int i = 0; i < M; i++) {
if (G[i].used) {
add(G[i].u, G[i].v, G[i].w);
add(G[i].v, G[i].u, G[i].w);
}
}
}
queue<int> que;
//计算出depth, d1, d2, fa.
void bfs() {
memset(depth, 0x3f3f3f3f, sizeof depth);
depth[0] = 0, depth[1] = 1;
que.push(1);
while (que.size()) {
int u = que.front();
que.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (depth[v] > depth[u] + 1) {
depth[v] = depth[u] + 1;
que.push(v);
fa[v][0] = u;
d1[v][0] = w[i], d2[v][0] = -INF;
for (int k = 1; k <= 16; k++) {
int anc = fa[v][k - 1];
fa[v][k] = fa[anc][k - 1];
d1[v][k] = d2[v][k] = -INF;
int dis[4] = { d1[v][k - 1], d2[v][k - 1], d1[anc][k - 1], d2[anc][k - 1] };
for (int j = 0; j < 4; j++) {
if (dis[j] > d1[v][k])
d2[v][k] = d1[v][k], d1[v][k] = dis[j];
else if (dis[j] != d1[v][k] && dis[j] > d2[v][k])
d2[v][k] = dis[j];
}
}
}
}
}
}
int lca(int a, int b, int w) {
static int dis[maxn * 2];
int cnt = 0;
if (depth[a] < depth[b]) swap(a, b);
for (int k = 16; k >= 0; k--) {
if (depth[fa[a][k]] >= depth[b]) {
dis[cnt++] = d1[a][k];
dis[cnt++] = d2[a][k];
a = fa[a][k];
}
}
if (a != b) {
for (int k = 16; k >= 0; k--) {
if (fa[a][k] != fa[b][k]) {
dis[cnt++] = d1[a][k];
dis[cnt++] = d2[a][k];
dis[cnt++] = d1[b][k];
dis[cnt++] = d2[b][k];
a = fa[a][k], b = fa[b][k];
}
dis[cnt++] = d1[a][0];
dis[cnt++] = d1[b][0];
}
}
int dist1 = -INF, dist2 = -INF;
for (int i = 0; i < cnt; i++) {
if (dis[i] > dist1) dist2 = dist1, dist1 = dis[i];
else if (dis[i] != dist1 && dis[i] > dist2) dist2 = dis[i];
}
if (w > dist1) return w - dist1;
if (w > dist2) return w - dist2;
return INF;
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 0; i < M; i++) {
scanf("%d%d%d", &G[i].u, &G[i].v, &G[i].w);
}
kruskal();
build();
bfs();
ll ans = 1e18;
for (int i = 0; i < M; i++) {
if (!G[i].used) {
int u = G[i].u, v = G[i].v, w = G[i].w;
ans = min(ans, sum + lca(u, v, w));
}
}
printf("%lld\n", ans);
return 0;
}
树上差分:352. 闇の連鎖
-
题意:Dark 有 N–1 条主要边,并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。另外,Dark 还有 M 条附加边。你的任务是把 Dark 斩为不连通的两部分。第一步需要切断一条主要边,第二步需要切断一条附加边.
-
我们定义题目所说的主要边为树边,附加边为非树边。任意一条非树边都可以和树边构成一个环。
-
假如一条树边不在图中的任何环上,那么把这条树边切断图就会不连通;若一条树边在一个环上,在切掉形成那个环的非树边就能变成不连通的图。但是在两个环上的话,就不可能切成不连通的图。
-
因此,我们枚举每条非树边,把构成的环上的每条树边的值 + 1 +1 +1。最后枚举每条树边,若 c = 0 c = 0 c=0,则 a n s + = M ans += M ans+=M;若 c = 1 c = 1 c=1,则 a n s + = 1 ans += 1 ans+=1;若 c > 1 c > 1 c>1,则 a n s + = 0 ans += 0 ans+=0.
-
问题就变成了:怎样快速给树上的一些边都增加一个值,怎样快速求出树上的边的值。
-
树上差分:设 x , y x, y x,y 是非树边的两个端点, x , y x, y x,y 的最近公共祖先是 p p p。则 d [ x ] + = c , d [ y ] + = c , d [ p ] − = 2 c d[x] += c, d[y] += c, d[p] -= 2c d[x]+=c,d[y]+=c,d[p]−=2c。树上差分的原理和数组差分差不多,都是为了方便修改某一个区间的值。其实沿着路径将对应的d数组的值加起来,就是这个地方对应的原本数组的值。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010, maxm = 2 * maxn;
int h[maxn], ne[maxm], e[maxm], idx;
int N, M, ans;
int d[maxn], depth[maxn], fa[maxn][17];
queue<int> que;
void bfs()
{
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[1] = 1;
que.push(1);
while (que.size()) {
int u = que.front(); que.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (depth[v] > depth[u] + 1) {
depth[v] = depth[u] + 1;
que.push(v);
fa[v][0] = u;
for (int k = 1; k <= 16; k++) fa[v][k] = fa[fa[v][k - 1]][k - 1];
}
}
}
}
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = 16; k >= 0; k--) {
if (depth[fa[a][k]] >= depth[b]) {
a = fa[a][k];
}
}
if (a == b) return a;
for (int k = 16; k >= 0; k--) {
if (fa[a][k] != fa[b][k]) {
a = fa[a][k];
b = fa[b][k];
}
}
return fa[a][0];
}
int dfs(int u, int father) {
int res = d[u];
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v == father) continue;
int s = dfs(v, u);
if (s == 0) ans += M;
else if (s == 1) ans++;
res += s;
}
return res;
}
int main() {
scanf("%d%d", &N, &M);
memset(h, -1, sizeof h);
for (int i = 1; i < N; i++) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
bfs();
for (int i = 0; i < M; i++) {
int a, b;
scanf("%d%d", &a, &b);
int p = lca(a, b);
d[a]++, d[b]++, d[p] -= 2;
}
dfs(1, -1);
printf("%d\n", ans);
return 0;
}