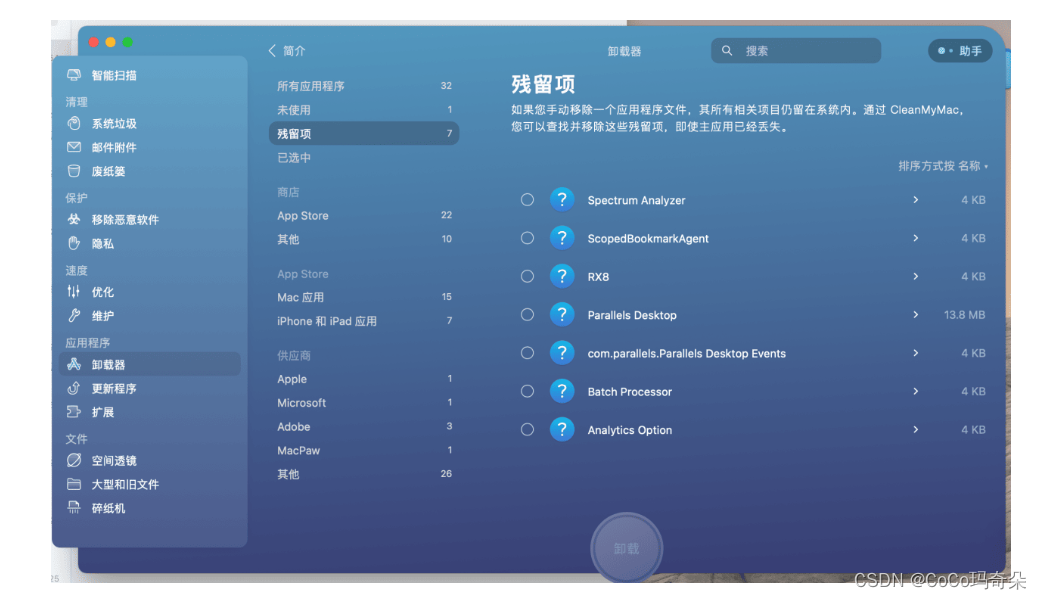
先看动图

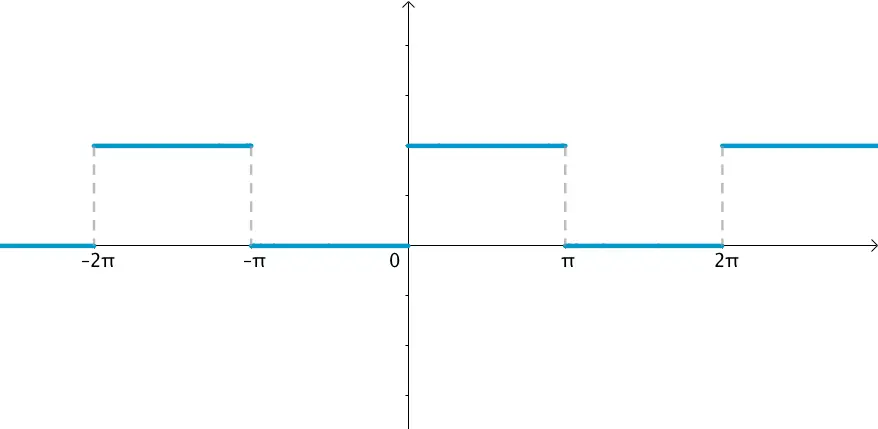
将函数f(x) 用 sin(nx) + cos(nx) 的形式表示出来的方式就是傅里叶级数

这里有几个使用条件

• 收敛性：符合迪力克雷收敛条件。简单理解为 f(x) 必须是一个丝滑的曲线。
• 周期性： f(x) 必须是一个周期函数

还有一个基础条件，三角函数具有正交性：任取两个不同三角函数元素，它们的乘积在[−π,π]上的定积分等于零。举例说明一共有如下四种情况（公式2、3、4种所列情况m不等于n）：

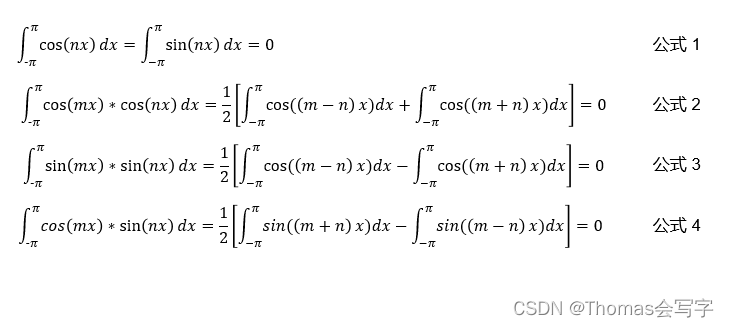
 这时，我们就可以吧符合条件的f(x) 写成傅里叶级数的样子： 

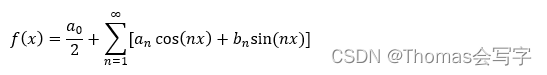
求解a0

我们对表达式两边在[−π,π]上求积分，得到 

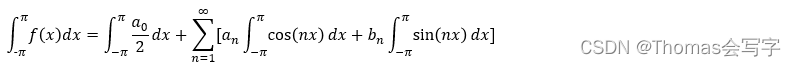
由公式1可知，上式中等号右侧除第一项外其余全为0。因此

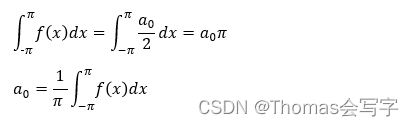
求解an

等式两端乘以 cos(kx)

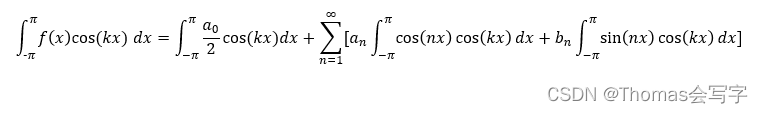由公式1、2、4，对于n不等于k的展开项，其积分值为0，因此等号右边只剩下n=k这一项：

 

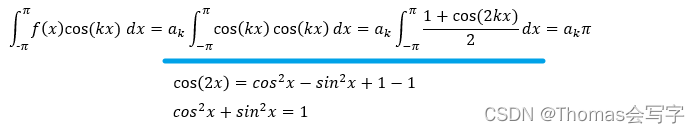
 求解bn

由求解an的方式可知，在等式两边同乘sin(kx)可求得

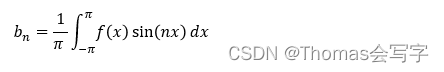
 此时，傅里叶级数的所有参数均可求得，对于需要展开的f(x)，可以写成

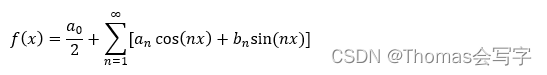
即，我们将直角坐标系上的周期函数曲线 f(x) 转移到了以sin cos 为底的坐标系中，也可以说将时域上的周期函数用频域的非周期函数表示出来。