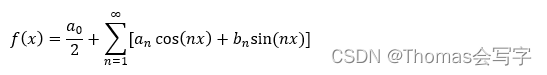参考文献：

[1]王月汉,刘文霞,姚齐,万海洋,何剑,熊雪君.面向配电网韧性提升的移动储能预布局与动态调度策略[J].电力系统自动化,2022,46(15):37-45.

1.基本原理

1. 1 目标函数

本文以最恶劣光伏出力场景下的移动储能配置成本与负荷削减成本最小为目标，建立两阶段鲁棒优化模型来确定移动储能的配置数量与位置。第一阶段的决策变量为移动储能与节点的连接状态以及线路开关状态，第二阶段的决策变量为负荷削减功率、分布式电源出力、节点电压、支路功率与电流，光伏出力为不确定变量，目标函数如下：

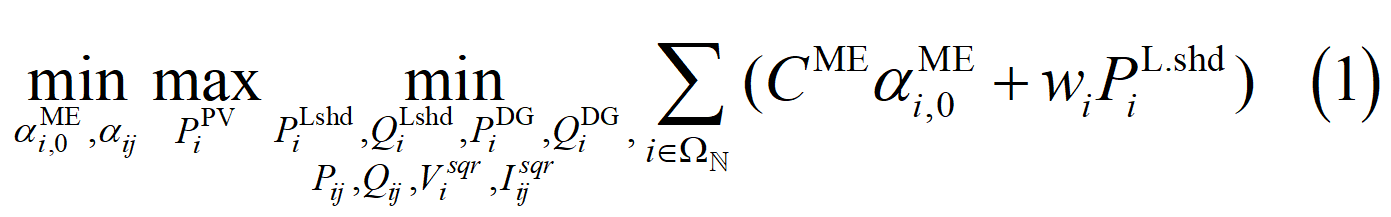
1. 2 约束条件

1. 2. 1 第一阶段约束

1）移动储能资源约束。在灾害发生前储备的移动储能资源有限，并且每台移动储能设备参数相同，每个节点最多预先配置一台设备，即

2）配电网辐射拓扑约束。考虑孤岛融合与无电源孤岛的情况，采用改进单商品流法确保恢复过程中配电网满足辐射状拓扑要求[19] ，通过引入虚拟源节点标志 0-1 变量，将网络重构后的孤岛数量加入优化过程，采用 Big-M 法对虚拟功率流进行松弛，具体表示如下：

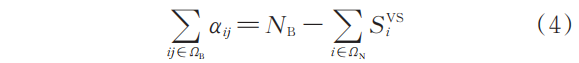
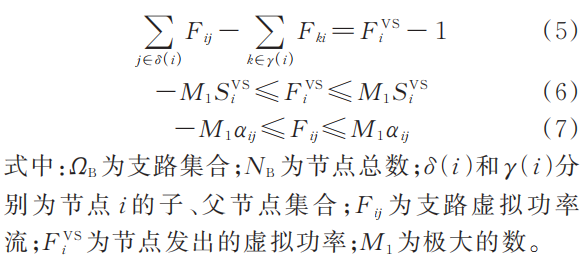
1. 2. 2 第二阶段约束

1）负荷削减约束。设负荷功率因数固定，负荷削减功率约束可表示如下：

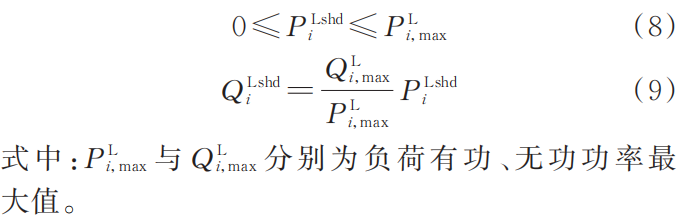
2）分布式电源出力约束。

各个节点的分布式电源出力不应超过其出力上限，假设在灾害发生前，移动储能、接入充电桩的电动汽车均处于满电状态，取充放电功率上限作为其出力上限。此外，分布式电源的有功功率、无功功率与功率因数之间存在约束，其中光伏采用定功率因数运行。分布式电源出力约束可表示如下：

3）配电网运行约束。对于辐射状配电网络，采用 DistFlow 潮流方程［20］，于网络拓扑结构随线路开关状态变化，因此，采用 Big-M 法对电压方程进行松弛。系统运行约束可表示如下：

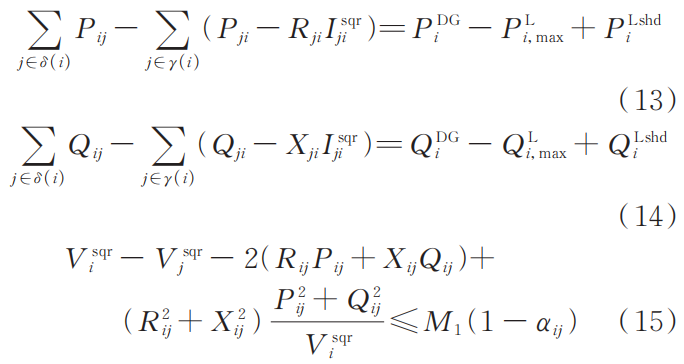
对于电压、电流和功率之间的非线性约束式（19），通过二阶锥松弛方法将其转化为以下二阶锥约束：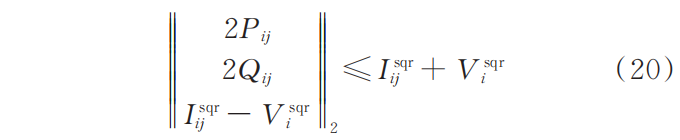

通过求解该两阶段优化模型，可以得到在最恶劣光伏出力场景下的移动储能配置数量、位置与网络拓扑方案，确保灾后移动储能迅速参与到负荷恢复过程中。

2 模型求解

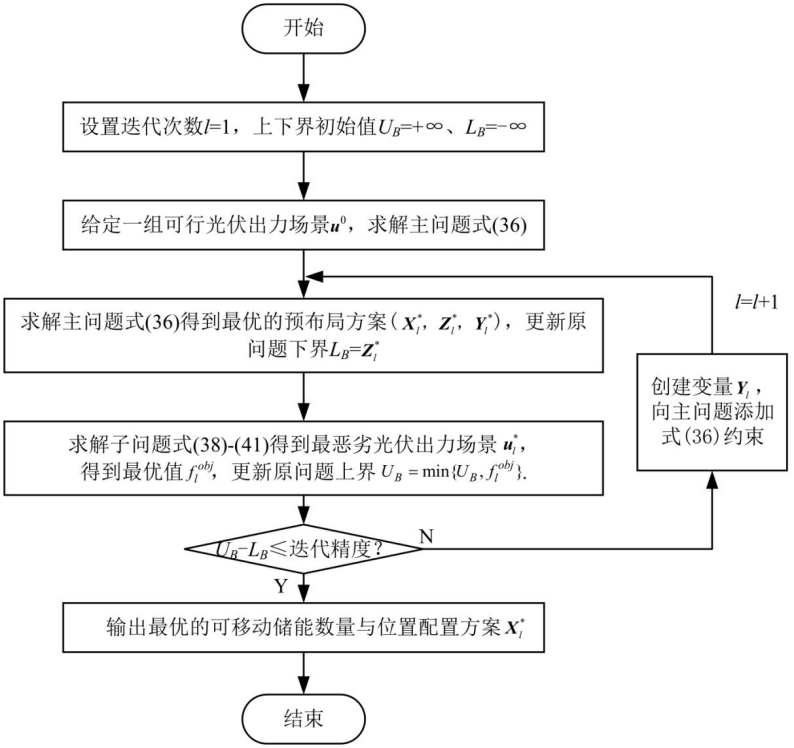
在给定电网-交通网融合系统参数条件下，通过求解灾前预布局鲁棒优化模型与多源协同的灾后恢复优化模型，获得最优的负荷削减与电源出力方案。其中，灾后恢复优化模型为混合整数二阶锥规划问题，可利用商业求解器 Gurobi 求解。对于灾前预防阶段的两阶段鲁棒优化模型，采用列约束生成（C&CG）算法求解，原问题的紧凑形式如下：

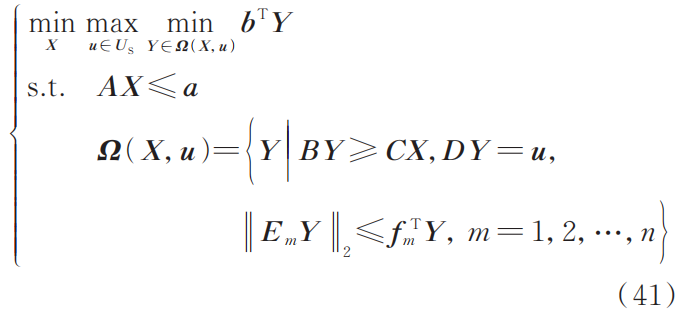
然后，将原问题分解为主问题与子问题，其中主问题求解给定光伏出力 u* 情况下最优的移动储能预布局方案，如式（42）所示，该混合整数二阶锥规划问题可通过商业求解器求解。

式中：Z 为辅助变量；K为最大迭代次数；下标l表示第l次迭代得到的变量。子问题求解给定移动储能预布局方案X *情况下最恶劣的光伏出力，子问题形式为：

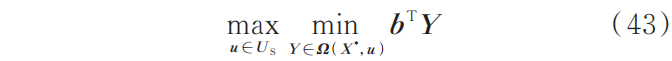子问题内层min问题为凸优化问题，根据强对偶理论将其转化为max形式［24］，与外层max问题合并形成如下单层优化问题：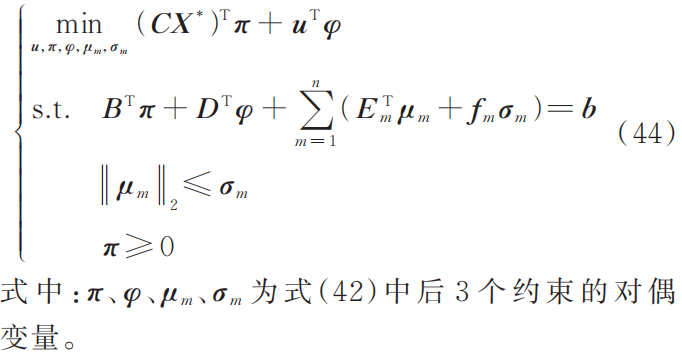

3.编程思路分析

3.1参数和变量定义

表1 相关参数

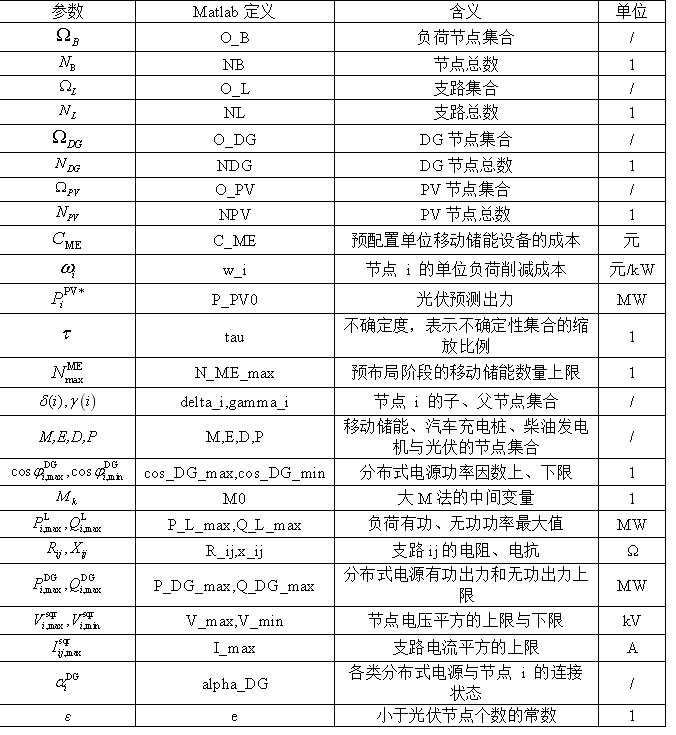
表2 决策变量

3.2编程思路

根据对文献内容的解读，可以设计下面的编程思路：

步骤1：输入所需数据

原文献中使用了标准IEEE33节点配电网，原始数据可以在Matpower工具箱的数据文件中找到，其他的相关数据原文献附录中基本已经提供，大体没啥问题。将所需的数据，按照表1的定义格式输入即可。

步骤2：定义决策变量

这一步比较简单，按照表2，初始化决策变量即可。要注意的是每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。

步骤3：定义目标函数和约束条件，尝试求解确定性优化问题

按照原文中给定的公式1-20，写出相应的目标函数与约束条件即可，需要注意的地方是在yalmip工具箱中，要转换为二阶锥优化，需要使用cone函数。

上述步骤都完成后，可以假设不确定变量保持不变，尝试求解一下确定性优化问题。如果能正常求解，则可进行下一步，否则需要反复调试，找到问题所在。

1.原文的约束条件(12)中，为约束DG的功率因数，引入了二次项，增大了模型求解难度。其实要表达功率因数上下限约束，写成P×tanφmax>Q>P×tanφmin即可，效果一样，但是可以避免引入二次项增加模型求解难度。

2.在这里强调一点，配电网最优潮流最容易踩坑的地方就是标幺值转换上。之前有朋友拿自己写的代码问我，说感觉公式模型都是按照参考文献打的，但一用求解器就是“Infeasible problem”，拿给我一看，参数中有的数值用的是实际值，有的数值用的是标幺值，非常混乱，我把参数统一修改为标幺值就可以正常运行了。建议在编程时都转换为标幺值求解。

步骤4：将目标函数、约束条件写成紧凑形式

确定性优化问题能正常求解后，就可以加入不确定变量，调试两阶段鲁棒优化问题是否能正常求解。为了便于两阶段鲁棒优化编程求解，需要把所有的系数写成紧凑的矩阵形式，所有的决策变量写成向量形式。这是因为两阶段鲁棒优化问题的子问题是一个双层优化问题，求解时一般需要通过对偶变换转为单层优化问题进行求解，一般变换过程都相当复杂，容易出错。但使用Matlab+Yalmip工具箱求解时，有三种更便捷的方法：

一是直接使用yalmip工具箱中的kkt函数(kkt - YALMIP)，通过KKT条件将双层优化问题转为单层优化问题。

二是直接使用yalmip工具箱中的dualize函数(dualize - YALMIP)，直接将原问题下层优化转为对偶问题，然后和上层优化合并形成单层优化。

三是采用yalmip内置的鲁棒优化求解方法(Robust optimization - YALMIP)，通过uncertain约束不确定变量，直接求解鲁棒优化问题，但这种方法要求不确定集为简单的盒装不确定集、椭圆不确定集或可通过1范数、2范数显式表达的不确定集。

这份代码为方便起见，采用kkt条件求解子问题，因此将目标函数、约束条件写成紧凑形式这一步可以省略。

关于式(41)的错误。从目标函数(1)中可以看到，目标函数中包括0-1变量以及连续变量，其中0-1变量包含在X中，连续变量包含在Y中，因此目标函数中应包括含有X的项以及含有Y的项，但式(41)中目标函数只与Y相关，应该是漏写了，代码中应该把这部分加上。

步骤5：求解两阶段鲁棒优化的主问题

关于决策变量。原文式(1)描述的比较清楚，第一阶段的决策变量为两个0-1变量，支路状态以及移动储能安装位置，不确定变量为光伏的出力，第二阶段决策变量为其余变量，可写成下列形式：

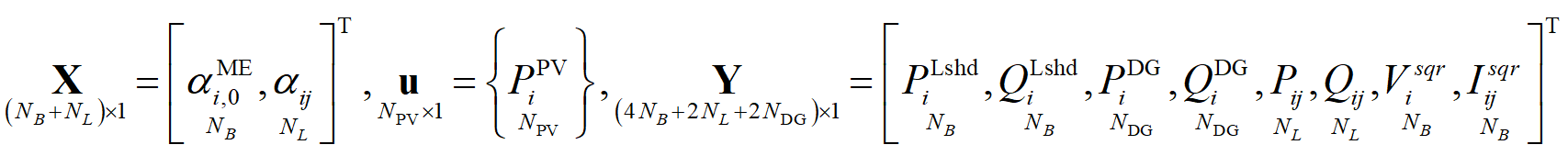
原文中用到的算例是改进的IEEE33节点配电网，NB为33，NL为37，NPV为5，NDG为10，因此变量X为70维列向量，变量u为5维列向量，变量Y为226维列向量。

在Matlab中编写主问题的求解函数时，输入参数应包括当前迭代次数(用于确定新增加的变量Yl和相应的约束条件)和不确定变量u的取值，输出参数包括决策变量X和LB。

步骤6：求解两阶段鲁棒优化的子问题

子问题是一个min-max的双层优化问题，文中用到对偶变换转为单层优化问题，具有一定的难度(求优化问题的系数矩阵和对偶转换比较困难)，代码中是采用yalmip编程的，直接用yalmip工具箱中的kkt函数就可以解出内层max问题的KKT条件，非常方便。这样就可以将min-max的双层优化子问题转为单层优化问题，并使用求解器求解。

在matlab编写子问题的函数时，输入参数应包括0-1决策变量X的取值，输出参数包括不确定变量u和UB。

步骤7：采用C&CG算法迭代求两阶段鲁棒优化问题最优解

有关算法的基本原理可以看我之前的博客(两阶段鲁棒优化及行列生成算法(C&CG)超详细讲解)。此处不再赘述。因为原文式(41)有点小问题，所以为了方便编程，可以重新写一下主问题和子问题。

主问题：

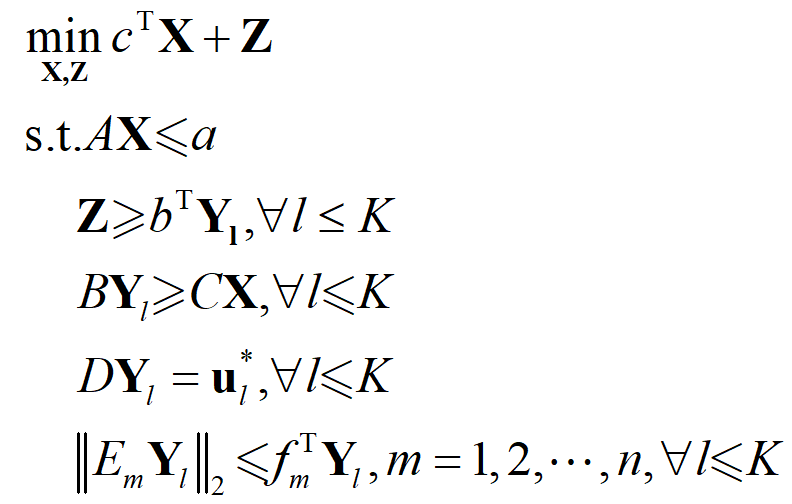
子问题：

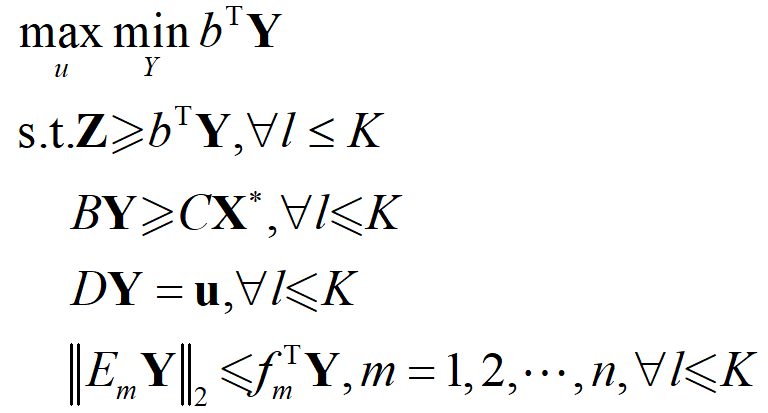
步骤8：输出计算结果

原文中将移动储能的预布局和优化调度拆成两阶段优化策略。预布局是第一阶段的优化，是一个基于混合整数二阶锥的两阶段鲁棒优化问题。这份代码复现了第一阶段灾前移动储能预布局的结果，后面的灾后多源协同的恢复优化模型，过几天有空了我也会解读并发到博客上。

4.完整Matlab代码

完整的matlab代码可以从这个链接获取：
面向配电网韧性提升的移动储能预布局与动态调度策略(1)-灾前布局matlab代码

5.运行结果分析

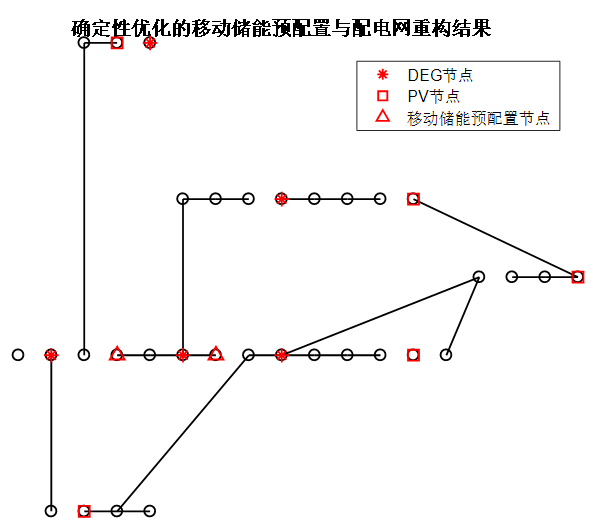
5.1确定性优化结果

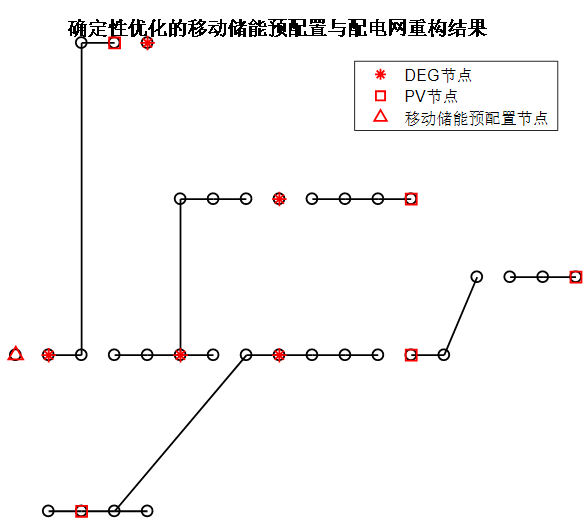
(1)考虑移动储能优化配置

(2)不考虑移动储能优化配置

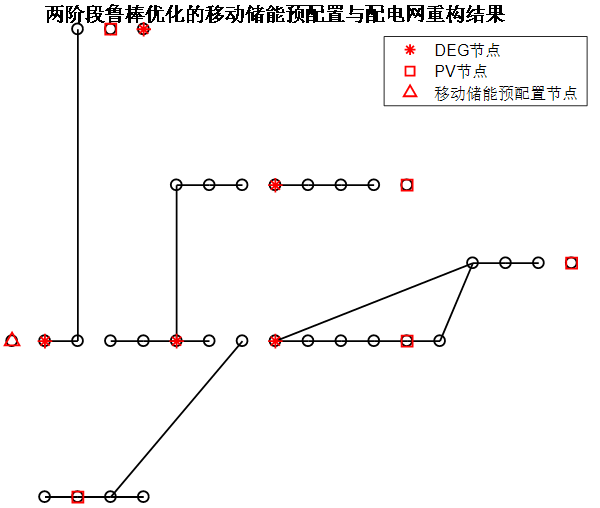
5.2 两阶段鲁棒优化结果

(1)考虑移动储能优化配置

(2)不考虑移动储能优化配置

几种结果的对比如下表所示：

场景		移动储能预配置节点	预布局成本/元
两阶段鲁棒优化	考虑移动储能预配置	节点4，7	4666.1668
两阶段鲁棒优化	不考虑移动储能预配置	节点1，1	8085.7385
确定性优化	考虑移动储能预配置	节点7，25	5085.8315
确定性优化	不考虑移动储能预配置	节点1，1	7665.8694