本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
文章目录
- 信道容量
- 信道容量的定义
- 信息传输率 R
- 信息传输速率
- 平均互信息
- 信道容量
- 三种特殊信道的容量
- 无噪无损信道
- 有噪无损信道
- 无噪有损信道
- 典型信道的信道容量
- BSC信道容量
- 连续信道的信道容量
- 单符号高斯连续信道
- 限频、限功率高斯信道的容量
- 单符号信号一>多符号多维信道
- Shannon信道编码定理
- 信源与信道的匹配
信道容量
写出并解释信道容量的定义
分析计算如下信道的信道容量
- 无噪无损信道
- 有噪无损信道
- 无噪有损信道
- 二进制对称信道
- AWGN信道
信道容量的定义
香农指出信道中的噪声对信道造成的根本限制是信道的传信率, 而不是可靠性。
信息传输率 R
我们研究信道的目的是要讨论信道中平均每个符号所能传送的信息量, 即信道的信息传输率 R , 即
R
=
I
(
X
;
Y
)
=
H
(
X
)
−
H
(
X
∣
Y
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
bit
/
symbol
\begin{aligned} R=I(X ; Y) & =H(X)-H(X \mid Y) \\ & =H(Y)-H(Y \mid X) \text { bit } / \text { symbol } \end{aligned}
R=I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X) bit / symbol
信息传输速率
若每个符号传输时间为
t
(
s
)
t(\mathrm{s})
t(s) , 则信道在单位时间内平均的信息量定义为信息传输速率
R
t
=
I
(
X
;
Y
)
t
b
i
t
/
s
R_{t}=\frac{I(X ; Y)}{t} \quad \mathrm{bit} / \mathrm{s}
Rt=tI(X;Y)bit/s
平均互信息
信道的信息传输率就是平均互信息
接收到符号 $\mathrm{Y} $ 后平均每个符号获得的关于
X
\mathrm{X}
X 的信息量。
I
(
X
;
Y
)
=
∑
i
∑
j
p
(
x
i
)
p
(
y
j
∣
x
i
)
log
p
(
y
j
∣
x
i
)
p
(
y
j
)
p
(
y
j
)
=
∑
i
=
1
n
p
(
x
i
)
p
(
y
j
∣
x
i
)
\begin{array}{l} I(X ; Y)=\sum_{i} \sum_{j} p(x_{i}) p(y_{j} \mid x_{i}) \log \frac{p(y_{j} \mid x_{i})}{p(y_{j})} \\ p(y_{j})=\sum_{i=1}^{n} p(x_{i}) p(y_{j} \mid x_{i}) \end{array}
I(X;Y)=∑i∑jp(xi)p(yj∣xi)logp(yj)p(yj∣xi)p(yj)=∑i=1np(xi)p(yj∣xi)
定理:
给定信道转移概率矩阵P后,平均互信息 I(X ; Y) 是输入信源的概率分布 p ( x ) p(\boldsymbol{x}) p(x) 的 ∩ \cap ∩ 型上凸函数。
信道容量是完全描述信道特性的参量,是信道能够传输的最大信息量。使 $ I(\boldsymbol{X} ; \boldsymbol{Y}) $ 达到最大的信源的概率分布 p ( x ) p(\boldsymbol{x}) p(x) 称为该信道的最佳输入分布。
信道容量
最大的信息传输率, 单位 bit/symbol
C = max p ( x i ) I ( X ; Y ) C=\max _{p(\boldsymbol{x}_{i})} I(X ; Y) C=p(xi)maxI(X;Y)
单位时间的信道容量, 单位 bit/s:
C = 1 T max p ( x i ) I ( X ; Y ) C=\frac{1}{T} \max _{p(x_{i})} I(X ; Y) C=T1p(xi)maxI(X;Y)
三种特殊信道的容量
无噪无损信道
输入输出一一对应, 信道无噪声无信息损失。
H
(
X
∣
Y
)
=
H
(
Y
∣
X
)
=
0
C
=
max
p
(
x
)
I
(
X
;
Y
)
=
max
p
(
x
)
{
H
(
X
)
−
H
(
X
∣
Y
)
}
=
max
p
(
x
)
H
(
X
)
=
logr
=
log
s
\begin{array}{c} H(X \mid Y)=H(Y \mid X)=0 \\ C=\max _{p(x)} I(X ; Y)=\max _{p(x)}\{H(X)-H(X \mid Y)\} \\ =\max _{p(x)} H(X)=\operatorname{logr}=\log s \end{array}
H(X∣Y)=H(Y∣X)=0C=maxp(x)I(X;Y)=maxp(x){H(X)−H(X∣Y)}=maxp(x)H(X)=logr=logs
其中$ \mathbf{r} $ 为信道输入符号个数,
s
\mathbf{s}
s 为信道输出符号个数,
r
=
s
\mathbf{r}=s
r=s 。最佳输入为等概输入。
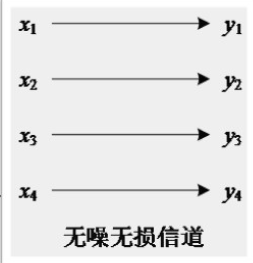
有噪无损信道
根据接收的符号, 可以完全确定发送符号, 无信息损失。
H
(
X
∣
Y
)
=
0
C
=
max
p
(
x
)
I
(
X
;
Y
)
=
max
p
(
x
)
{
H
(
X
)
−
H
(
X
∣
Y
)
}
=
max
p
(
x
)
H
(
X
)
=
logr
\begin{array}{c} H(X \mid Y)=0 \\ C=\max _{p(x)} I(X ; Y)=\max _{p(x)}\{H(X)-H(X \mid Y)\} \\ =\max _{p(x)} H(X)=\operatorname{logr} \end{array}
H(X∣Y)=0C=maxp(x)I(X;Y)=maxp(x){H(X)−H(X∣Y)}=maxp(x)H(X)=logr
最佳输入为等概输入

无噪有损信道
发送不会出错, 无噪声。但是根据接收符号, 无法准确判断发送符号, 有信息损失。
H
(
Y
∣
X
)
=
0
C
=
max
p
(
x
)
I
(
X
;
Y
)
=
max
p
(
x
)
{
H
(
Y
)
−
H
(
Y
∣
X
)
}
=
max
p
(
x
)
H
(
Y
)
=
logs
\begin{array}{c} H(Y \mid X)=0 \\ C=\max _{p(x)} I(X ; Y)=\max _{p(x)}\{H(Y)-H(Y \mid X)\} \\ =\max _{p(x)} H(Y)=\operatorname{logs} \end{array}
H(Y∣X)=0C=maxp(x)I(X;Y)=maxp(x){H(Y)−H(Y∣X)}=maxp(x)H(Y)=logs
最佳输入为使输出等概。
典型信道的信道容量
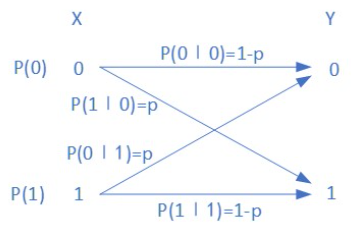
BSC信道容量
设二进制对称信道的输入概率空间为
[
X
P
]
=
[
0
1
ω
ω
ˉ
]
[\begin{array}{l} X \\ P \end{array}]=[\begin{array}{cc} 0 & 1 \\ \omega & \bar{\omega} \end{array}]
[XP]=[0ω1ωˉ]
信道矩阵:
P
=
[
1
−
p
p
p
1
−
p
]
=
[
p
ˉ
p
p
p
ˉ
]
P=[\begin{array}{cc} 1-p & p \\ p & 1-p \end{array}]=[\begin{array}{ll} \bar{p} & p \\ p & \bar{p} \end{array}]
P=[1−ppp1−p]=[pˉpppˉ]
p
(
y
=
0
)
=
∑
i
=
0
1
p
(
x
i
)
p
(
y
0
∣
x
i
)
=
ω
p
ˉ
+
ω
ˉ
p
p
(
y
=
1
)
=
∑
i
=
0
1
p
(
x
i
)
p
(
y
1
∣
x
i
)
=
ω
p
+
ω
ˉ
p
ˉ
H
(
Y
)
=
(
ω
p
ˉ
+
ω
ˉ
p
)
log
1
ω
p
ˉ
+
ω
ˉ
p
+
(
ω
p
+
ω
ˉ
p
ˉ
)
log
1
ω
p
+
ω
ˉ
p
ˉ
=
H
(
ω
p
ˉ
+
ω
ˉ
p
)
\begin{array}{l} p(y=0)=\sum_{i=0}^{1} p(x_{i}) p(y_{0} \mid x_{i})=\omega \bar{p}+\bar{\omega} p \\ p(y=1)=\sum_{i=0}^{1} p(x_{i}) p(y_{1} \mid x_{i})=\omega p+\bar{\omega} \bar{p} \\ H(Y) \\ =(\omega \bar{p}+\bar{\omega} p) \log \frac{1}{\omega \bar{p}+\bar{\omega} p}+(\omega p+\bar{\omega} \bar{p}) \log \frac{1}{\omega p+\bar{\omega} \bar{p}} \\ =H(\omega \bar{p}+\bar{\omega} p) \end{array}
p(y=0)=∑i=01p(xi)p(y0∣xi)=ωpˉ+ωˉpp(y=1)=∑i=01p(xi)p(y1∣xi)=ωp+ωˉpˉH(Y)=(ωpˉ+ωˉp)logωpˉ+ωˉp1+(ωp+ωˉpˉ)logωp+ωˉpˉ1=H(ωpˉ+ωˉp)
H ( Y ∣ X ) = − ∑ i p ( x i ) ∑ j p ( y j ∣ x i ) log p ( y j ∣ x i ) = − ∑ j p ( y j ∣ x i ) log p ( y j ∣ x i ) = − [ p log p + p ˉ log p ] = H ( p ) I ( X ; Y ) = H ( Y ) − H ( Y ∣ X ) = H ( ω p ˉ + ω ˉ p ) − H ( p ) ≤ 1 − H ( p ) \begin{array}{l} H(Y \mid X)=-\sum_{i} p(x_{i}) \sum_{j} p(y_{j} \mid x_{i}) \log p(y_{j} \mid x_{i}) \\ =-\sum_{j} p(y_{j} \mid x_{i}) \log p(y_{j} \mid x_{i})=-[p \log p+\bar{p} \log p] \\ =H(p) \\ I(X ; Y)=H(Y)-H(Y \mid X)=H(\omega \bar{p}+\bar{\omega} p)-H(p) \\ \leq 1-H(p) \end{array} H(Y∣X)=−∑ip(xi)∑jp(yj∣xi)logp(yj∣xi)=−∑jp(yj∣xi)logp(yj∣xi)=−[plogp+pˉlogp]=H(p)I(X;Y)=H(Y)−H(Y∣X)=H(ωpˉ+ωˉp)−H(p)≤1−H(p)
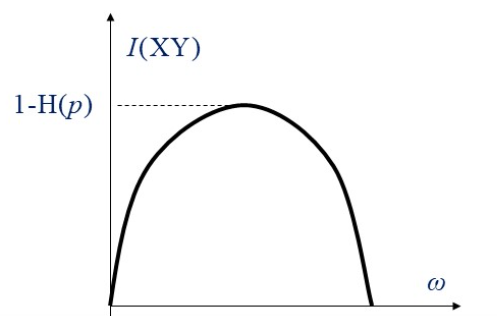
当 p 固定时, I(X ; Y) 是 ω \omega ω 的 ∩ \cap ∩ 型上凸函数。
I
(
X
;
Y
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
=
H
(
ω
p
ˉ
+
ω
ˉ
p
)
−
H
(
p
)
≤
1
−
H
(
p
)
\begin{array}{l} I(X ; Y)=H(Y)-H(Y \mid X) \\ =H(\omega \bar{p}+\bar{\omega} p)-H(p) \\ \leq 1-H(p) \end{array}
I(X;Y)=H(Y)−H(Y∣X)=H(ωpˉ+ωˉp)−H(p)≤1−H(p)
I(X, Y) 对
ω
\omega
ω 存在一个极大值,该极大值为信源的压缩极限。
BSC 信道容量 $C=1-H§ $
当固定信源的概率分布 ω \omega ω 时, I ( X ; Y ) I(X ; Y) I(X;Y) 是 p 的U型下凸函数。
- 当
p
=
0
\boldsymbol{p}=\mathbf{0}
p=0 ,
$C=1-0=1 bit =H(X) $ (信道无噪声) - 当
p
=
1
/
2
p=1 / 2
p=1/2 ,
$C=1-H(\frac{1}{2}, \frac{1}{2})=0 $ (信道强噪声)

当信源输入符号的速率为
r
s
r_{s}
rs (符号/秒), 信道容量
C
t
=
r
s
[
1
−
H
(
p
)
]
C_{t}=r_{s}[1-H(p)]
Ct=rs[1−H(p)]
实际信息传输速率
R
t
R_{t}
Rt 为
R
t
=
r
s
[
H
(
X
)
−
H
(
X
∣
Y
)
]
R_{t}=r_{s}[H(X)-H(X \mid Y)]
Rt=rs[H(X)−H(X∣Y)]
进入信道输入端的信息速率
D
in
=
r
s
H
(
X
)
D_{\text {in }}=r_{s} H(X)
Din =rsH(X)
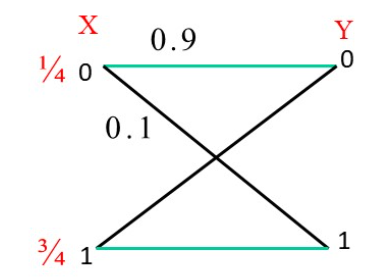
BSC信道如下图, r s = 1000 r_{s}=1000 rs=1000 符号/秒,错误传递概率 p = 0.1 p=0.1 p=0.1 求:信道容量和实际信息传输速率。
C t = r s [ 1 − H ( p ) ] = 1000 [ 1 + ( 0.1 log 0.1 + 0.9 log 0.9 ) ] = 1000 [ 1 − 0.469 ] = 531 b i t / s \begin{aligned} C_{t} & =r_{s}[1-H(p)] \\ & =1000[1+(0.1 \log 0.1+0.9 \log 0.9)] \\ & =1000[1-0.469]=531 \mathrm{bit} / \mathrm{s} \end{aligned} Ct=rs[1−H(p)]=1000[1+(0.1log0.1+0.9log0.9)]=1000[1−0.469]=531bit/s
信道实际信息传输速率R t = r s [ H ( X ) − H ( X ∣ Y ) ] = 1000 × [ 0.811 − 0.398 ] = 413 b i t / s D i n = r s H ( X ) = 1000 × 0.811 = 811 b i t / s \begin{array}{l} R_{t}=r_{s}[H(X)-H(X \mid Y)] \\ =1000 \times[0.811-0.398]=413 \mathrm{bit} / \mathrm{s} \\ D_{i n}=r_{s} H(X)=1000 \times 0.811=811 \mathrm{bit} / \mathrm{s} \end{array} Rt=rs[H(X)−H(X∣Y)]=1000×[0.811−0.398]=413bit/sDin=rsH(X)=1000×0.811=811bit/s
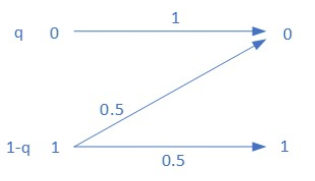
解: I ( X ; Y ) = H ( Y ) − H ( Y ∣ X ) I(X ; Y)=H(Y)-H(Y \mid X) I(X;Y)=H(Y)−H(Y∣X)
H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) = q H ( Y ∣ X = 0 ) + ( 1 − q ) H ( Y ∣ X = 1 ) \begin{aligned} H(Y \mid X) & =\sum_{x} p(x) H(Y \mid X=x) \\ & =q H(Y \mid X=0)+(1-q) H(Y \mid X=1) \end{aligned} H(Y∣X)=x∑p(x)H(Y∣X=x)=qH(Y∣X=0)+(1−q)H(Y∣X=1)
因为:
H ( Y ∣ X = 0 ) = p ( 0 ∣ x = 0 ) log p ( 0 ∣ x = 0 ) + p ( 1 ∣ x = 0 ) log p ( 1 ∣ x = 0 ) = 1 log 1 + 0 log 0 = 0 H ( Y ∣ X ) = ( 1 − q ) H ( Y ∣ X = 1 ) = ( 1 − q ) h ( 0.5 ) = 1 − q \begin{array}{l} H(Y \mid X=0) \\ =p(0 \mid x=0) \log p(0 \mid x=0)+p(1 \mid x=0) \log p(1 \mid x=0) \\ =1 \log 1+0 \log 0=0 \\ H(Y \mid X)=(1-q) H(Y \mid X=1)=(1-q) h(0.5)=1-q \end{array} H(Y∣X=0)=p(0∣x=0)logp(0∣x=0)+p(1∣x=0)logp(1∣x=0)=1log1+0log0=0H(Y∣X)=(1−q)H(Y∣X=1)=(1−q)h(0.5)=1−qp ( Y = 0 ) = q p ( Y = 0 ∣ X = 0 ) + ( 1 − q ) p ( Y = 0 ∣ X = 1 ) = q + ( 1 − q ) × 0.5 = 0.5 + 0.5 q p ( Y = 1 ) = q p ( Y = 1 ∣ X = 0 ) + ( 1 − q ) p ( Y = 1 ∣ X = 1 ) = ( 1 − q ) × 0.5 = 0.5 − 0.5 q \begin{array}{l} p(Y=0) \\ =q p(Y=0 \mid X=0)+(1-q) p(Y=0 \mid X=1) \\ =q+(1-q) \times 0.5=0.5+0.5 q p(Y=1)=q \\ p(Y=1 \mid X=0)+(1-q) p(Y=1 \mid X=1) \\ =(1-q) \times 0.5=0.5-0.5 q \end{array} p(Y=0)=qp(Y=0∣X=0)+(1−q)p(Y=0∣X=1)=q+(1−q)×0.5=0.5+0.5qp(Y=1)=qp(Y=1∣X=0)+(1−q)p(Y=1∣X=1)=(1−q)×0.5=0.5−0.5q
故:
C = max q [ H ( 0.5 − 0.5 q ) − ( 1 − q ) ] \mathrm{C}=\max _{q}[H(0.5-0.5 q)-(1-q)] C=qmax[H(0.5−0.5q)−(1−q)]
令 d C d q = 0 \frac{d C}{d q}=0 dqdC=0 , 有 q = 3 5 = 0.6 q=\frac{3}{5}=0.6 q=53=0.6
C = h ( 0.2 ) − 0.4 = 0.3219 C=h(0.2)-0.4=0.3219 C=h(0.2)−0.4=0.3219
连续信道的信道容量
单符号高斯连续信道
输入为连续随机变量
X
∈
(
−
∞
,
∞
)
X \in(-\infty, \infty)
X∈(−∞,∞) ,输出为
Y
=
X
+
n
Y=X+n
Y=X+n,
n
n
n : 均值为 0 , 方差为
σ
2
\sigma^{2}
σ2 的高斯变量, 与 X 统计独立。由条件概率可知, 当 X 已知时, Y 也为正态变量, 均值为 0 , 方差为
σ
2
\sigma^{2}
σ2 ,
p
(
y
∣
x
)
=
1
2
π
σ
2
exp
[
−
1
2
σ
2
(
y
−
x
)
2
]
p(y \mid x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp [-\frac{1}{2 \sigma^{2}}(y-x)^{2}]
p(y∣x)=2πσ21exp[−2σ21(y−x)2]
I [ X ; Y , p ( x ) ] = H ( Y ) − ∫ − ∞ ∞ p ( x ) ∫ − ∞ ∞ p ( y ∣ x ) log p ( y ∣ x ) d y d x = H ( Y ) − ∫ − ∞ ∞ p ( x ) log ( 2 π e σ ) d x = H ( Y ) − log ( 2 π e σ ) \begin{array}{l} I[X ; Y, p(x)] \\ =H(Y)-\int_{-\infty}^{\infty} p(x) \int_{-\infty}^{\infty} p(y \mid x) \log p(y \mid x) d y d x \\ =H(Y)-\int_{-\infty}^{\infty} p(x) \log (\sqrt{2 \pi e} \sigma) d x \\ =H(Y)-\log (\sqrt{2 \pi e} \sigma) \end{array} I[X;Y,p(x)]=H(Y)−∫−∞∞p(x)∫−∞∞p(y∣x)logp(y∣x)dydx=H(Y)−∫−∞∞p(x)log(2πeσ)dx=H(Y)−log(2πeσ)
注: p(x) 高斯分布, 则有
∫
−
∞
∞
p
(
x
)
log
p
(
x
)
d
x
=
log
(
2
π
e
σ
)
\int_{-\infty}^{\infty} p(x) \log p(x) d x=\log (\sqrt{2 \pi e} \sigma)
∫−∞∞p(x)logp(x)dx=log(2πeσ)
当信道输入功率为时
P
W
i
P_{W i}
PWi , 输出功率可表示为
P
W
o
P_{W o}
PWo , 且输入与噪声独立时
P
W
o
=
P
W
i
+
σ
2
P_{W o}=P_{W i}+\sigma^{2}
PWo=PWi+σ2
使 H(Y) 最大的 Y 是均值为 0 的正态分布随机变量。而由
Y
=
X
+
n
Y=X+n
Y=X+n 可知,
X
X
X 也应该为均值为零方差为
P
W
i
P_{W_{i}}
PWi 的随机变量。所以
C
=
log
2
π
e
P
W
o
−
log
2
π
e
σ
2
=
1
2
log
P
W
o
σ
2
=
1
2
log
(
1
+
P
W
i
σ
2
)
C=\log \sqrt{2 \pi e P_{W o}}-\log \sqrt{2 \pi e \sigma^{2}}=\frac{1}{2} \log \frac{P_{W o}}{\sigma^{2}}=\frac{1}{2} \log (1+\frac{P_{W i}}{\sigma^{2}})
C=log2πePWo−log2πeσ2=21logσ2PWo=21log(1+σ2PWi)
如不限制输入信号,
H
(
H
)
H(\boldsymbol{H})
H(H) 、
P
W
o
P_{W_{o}}
PWo 可趋于无限, 此时信道容量无限大一一实际不可行。
限频、限功率高斯信道的容量
信道输入信号为平稳随机过程 X ( t ) X(t) X(t) , 加性干扰为 n ( t ) n(t) n(t) , 输出为 Y ( t ) = X ( t ) + n ( t ) Y(t)=X(t)+n(t) Y(t)=X(t)+n(t) 。输入信号功率受限, 即 E [ X 2 ( t ) ] ≤ S E[X^{2}(t)] \leq S E[X2(t)]≤S 。
限带信道的频率特性:
H ( f ) = { 1 , ∣ f ∣ < B 0 , ∣ f ∣ > B . H(f)=\{\begin{array}{ll} 1, & |f|<B \\ 0, & |f|>B \end{array}. H(f)={1,0,∣f∣<B∣f∣>B.
$ Y(t), X(t), n(t)$ 的带宽为 B , 以 2B 采样,得
Y
(
t
1
)
,
Y
(
t
2
)
,
…
Y(t_{1}), Y(t_{2}), \ldots
Y(t1),Y(t2),… ,
$ Y(t_{n}), \ldots, Y(t_{L}) \ldots, X(t_{1}), X(t_{2}), \ldots, X(t_{n}), \ldots, X(t_{L}) \ldots, n(t_{1}), n(t_{2}), \ldots ,
n(t_{n}), \ldots, n(t_{L}) \ldots$ 。时刻
t
n
,
Y
(
t
n
)
=
X
(
t
n
)
+
n
(
t
n
)
t_{n}, Y(t_{n})=X(t_{n})+n(t_{n})
tn,Y(tn)=X(tn)+n(tn) 。
由单符号高斯信道容量公式可得
C = max p ( x ) [ I ( X ( t n ) , Y ( t n ) , p ( x ) ) ] = 1 2 log ( 1 + s σ 2 ) \begin{aligned} C & =\max _{p(x)}[I(X(t_{n}), Y(t_{n}), p(x))] \\ & =\frac{1}{2} \log (1+\frac{s}{\sigma^{2}}) \end{aligned} C=p(x)max[I(X(tn),Y(tn),p(x))]=21log(1+σ2s)
上式中 S σ 2 \frac{S}{\sigma^{2}} σ2S 为信号功率与噪声功率的比, 也即信噪比 , 其中 S = E [ X 2 ( t n ) ] , σ 2 = E [ n 2 ( t n ) ] S=E[X^{2}(t_{n})], \sigma^{2}=E[n^{2}(t_{n})] S=E[X2(tn)],σ2=E[n2(tn)] 。
单符号信号一>多符号多维信道
X
L
,
Y
L
X_{L}, Y_{L}
XL,YL 分别表示 L 个抽样
X
(
t
n
)
,
Y
(
t
n
)
(
n
=
1
,
2
,
…
,
L
)
X(t_{n}), Y(t_{n}) (n=1,2, \ldots, L)
X(tn),Y(tn)(n=1,2,…,L) 的 L 维向量, 则对多符号信道
I
(
X
L
,
Y
L
)
≤
L
2
log
(
1
+
S
σ
2
)
I(X_{L}, Y_{L}) \leq \frac{L}{2} \log (1+\frac{S}{\sigma^{2}})
I(XL,YL)≤2Llog(1+σ2S)
当
X
(
t
n
)
,
Y
(
t
n
)
X(t_{n}), Y(t_{n})
X(tn),Y(tn) 统计独立时
max
[
I
(
X
L
,
Y
L
)
]
=
L
2
log
(
1
+
S
σ
2
)
\max [I(X_{L}, Y_{L})]=\frac{L}{2} \log (1+\frac{S}{\sigma^{2}})
max[I(XL,YL)]=2Llog(1+σ2S)
T 时间内抽样数 L=2BT , 则信道传输最大信息量
C
T
=
B
T
log
(
1
+
S
σ
2
)
C_{T}=B T \log (1+\frac{S}{\sigma^{2}})
CT=BTlog(1+σ2S)
对连续信道, 定义单位时间内传送的最大信息量为信道容量
C
=
C
T
T
=
B
log
(
1
+
S
σ
2
)
C=\frac{C_{T}}{T}=B \log (1+\frac{S}{\sigma^{2}})
C=TCT=Blog(1+σ2S)
限频、限功率高斯信道的信道容量公式, 也即 Shannon公式。
香农公式的另一种表达: 因为 $\lim _{x arrow 0} \frac{1}{x} \log (1+x)=\log _{2} e \approx 1.44 $, 所以 lim B a r r o w ∞ C ≈ 1.44 S N 0 \lim _{B arrow \infty} C \approx 1.44 \frac{S}{N_{0}} limBarrow∞C≈1.44N0S 。
C = B log ( 1 + S N 0 B ) b i t / s , N 0 C=B \log (1+\frac{S}{N_{0} B}) b i t / s, N_{0} C=Blog(1+N0BS)bit/s,N0 为限带高斯白噪声 n(t) 的单边功率谱密度。
当 S a r r o w ∞ S arrow \infty Sarrow∞ 时, C a r r o w ∞ C arrow \infty Carrow∞ ; 当 $ B arrow \infty$ 时, C a r r o w C arrow Carrow 一确定值。
C = B log ( 1 + S N 0 B ) = S N 0 N 0 B S log ( 1 + S N 0 B ) lim B a r r o w ∞ C = S N 0 lim B a r r o w ∞ [ N 0 B S log ( 1 + S N 0 B ) ] ≈ 1.44 S N 0 \begin{array}{c} C=B \log (1+\frac{S}{N_{0} B})=\frac{S}{N_{0}} \frac{N_{0} B}{S} \log (1+\frac{S}{N_{0} B}) \\ \lim _{B arrow \infty} C=\frac{S}{N_{0}} \lim _{B arrow \infty}[\frac{N_{0} B}{S} \log (1+\frac{S}{N_{0} B})] \approx 1.44 \frac{S}{N_{0}} \end{array} C=Blog(1+N0BS)=N0SSN0Blog(1+N0BS)limBarrow∞C=N0SlimBarrow∞[SN0Blog(1+N0BS)]≈1.44N0S
当 C ∞ = 1 b i t / s C_{\infty}=1 \mathrm{bit} / \mathrm{s} C∞=1bit/s ,有 P s N 0 = ln 2 = 0.693 ∼ − 1.6 d B \frac{P_{s}}{N_{0}}=\ln 2=0.693 \sim-1.6 d B N0Ps=ln2=0.693∼−1.6dB ,即带宽不受限制时, 传输1bit信息, 信噪比最低只需要-1.6dB, 这是加性高斯噪声信道信息传输速率的极限值, 是一切编码方式所能达到的理论极限。
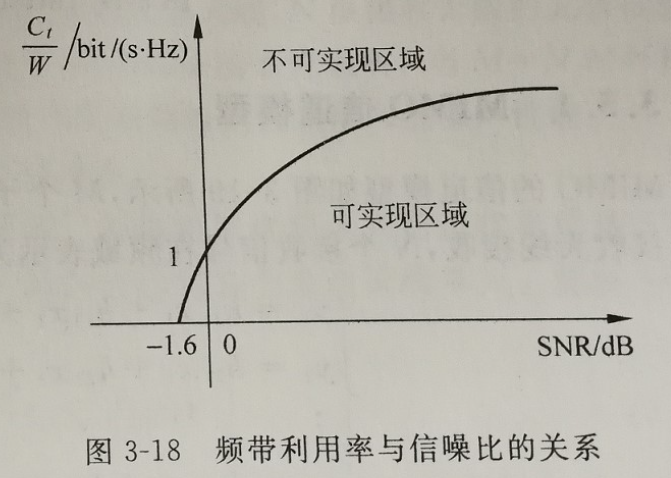
γ = C t W = log ( 1 + S N R ) b p s / H z \gamma=\frac{C_{t}}{W}=\log (1+S N R) b p s / H z γ=WCt=log(1+SNR)bps/Hz– 单位频带的信息传输速率(频带利用率)。
当 γ a r r o w 0 \gamma arrow 0 γarrow0 时, S N R = − 1.6 d B \mathrm{SNR}=-1.6 \mathrm{~dB} SNR=−1.6 dB , 此时信道完全丧失通信能力。

小结:
保证一定的信道容量的带宽 B 和信噪比 S / N 0 S / N_{0} S/N0 可以互换, 即增加带宽 可以降低必须的信橾比, 或增加信噪比也可以降低所必须的带宽。
Shannon信道编码定理
揭示了信源信息速率与信道容量的关系
如果信源的信息率 (即每秒发出的信息量)小于信道容量, 则存在一种编码方式, 可保证通过该信道传送信息的差错率任意小;反之 , 如果信源的信息率大于信道容量, 则不可能存在此种编码方式, 传送信息的差错率将很大。
现设计一个M进制数字通信系统,要求码元速率为 1 0 4 10^{4} 104 波特。已知信道为 $ A W G N $ 信道,带宽为 10 k H z 10 \mathrm{kHz} 10kHz , 噪声的功率谱密度为 N 0 = 1 × 1 0 − 12 W / H z N_{0}=1 \times 10^{-12} \mathrm{~W} / \mathrm{Hz} N0=1×10−12 W/Hz , 系统最大发送功率为 10 W 10 \mathrm{~W} 10 W ,信道衰减 80 d B 80 \mathrm{~dB} 80 dB 。问 M \mathrm{M} M 最大取值是多少?
解: $C=B \log (1+\frac{S}{N}) $
10 lg ( P T P R ) = 10 lg ( 10 / P R ) = 80 a r r o w P R = 1 0 − 7 W 10 \lg (\frac{P_{T}}{P_{R}})=10 \lg (10 / P_{R})=80 arrow P_{R}=10^{-7} \mathrm{~W} 10lg(PRPT)=10lg(10/PR)=80arrowPR=10−7 W故
S N = 1 0 − 7 1 × 1 0 − 12 × 1 0 4 = 10 C = B log ( 1 + S N ) ≈ 3.46 × 1 0 4 b i t / s C ≥ R B × log M a r r o w 3.46 × 1 0 4 ≥ 1 0 4 × log M a r r o w M ≤ 3.46 \begin{array}{c} \frac{S}{N}=\frac{10^{-7}}{1 \times 10^{-12} \times 10^{4}}=10 \\ C=B \log (1+\frac{S}{N}) \approx 3.46 \times 10^{4} \mathrm{bit} / \mathrm{s} \\ C \geq R_{B} \times \log M arrow 3.46 \times 10^{4} \geq 10^{4} \times \log M arrow M \leq 3.46 \end{array} NS=1×10−12×10410−7=10C=Blog(1+NS)≈3.46×104bit/sC≥RB×logMarrow3.46×104≥104×logMarrowM≤3.46
故:M最大取值为 8 。
信源与信道的匹配
信道的信息的传输速率 R \mathbf{R} R 与信源分布密切相关。
R = C \mathbf{R}=\mathbf{C} R=C , 信源与信道匹配。
R ≠ C \mathbf{R} \neq \mathbf{C} R=C , 信源与信道不匹配, 信道有冗余
定义
信道冗余度
=
C
−
I
(
X
;
Y
)
信道冗余度 = C - I (X ; Y)
信道冗余度=C−I(X;Y)
其中
I
(
X
;
Y
)
I(X ; Y)
I(X;Y) 是信道实际通过的平均信息速率
信道相对冗余度
=
1
−
I
(
X
;
Y
)
C
信道相对冗余度 =1-\frac{I(X ; Y)}{C}
信道相对冗余度=1−CI(X;Y)
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.