一、多元向量的泰勒级数展开

$$\{\begin{array}{c}{y}_1=f_1(\mathbf{X})=f_1\left(x_1,x_2,\cdots x_n\right)\\ y_2=f_2(\mathbf{X})=f_2\left(x_1,x_2,\cdots x_n\right)\\ ⋮\\ y_m=f_m(\mathbf{X})=f_m\left(x_1,x_2,\cdots x_n\right)\end{array}$$

上面线性方差组，写成向量形式就是：
$$\mathbf{Y}=\mathbf{f}\left(\mathbf{X}\right)$$
泰勒展开式为：
$$\mathbf{Y}=\mathbf{f}\left({\mathbf{X}}^{(0)}\right)+\sum _{i=1}^{\infty }\frac{1}{i!}{\left({\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\right)}^i\mathbf{f}\left({\mathbf{X}}^{(0)}\right)$$
其中 $\delta \mathbf{X}=\mathbf{X}-{\mathbf{X}}^{(0)}$ ，$\nabla ={\left[\begin{array}{llll}\frac{\partial }{\partial x1}& \frac{\partial }{\partial x2}& \cdots & \frac{\partial }{\partial x_n}\end{array}\right]}^{\mathrm{T}}$

一阶导代表梯度、二阶导代表曲率半径

一阶展开项的详细展开式：

标量的求导运算对向量求导是对向量里的每一个元素求导，$m$ 列多元函数对 $n$ 行的自变量求导：
$$\begin{array}{l}\frac{1}{1}{\left({\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\right)}^{\prime }\mathbf{f}\left({\mathbf{X}}^{(0)}\right)={\left(\frac{\partial }{\partial x_1}\delta x_1+\frac{\partial }{\partial x_2}\delta x_2+\cdots +\frac{\partial }{\partial x_n}\delta x_n\right)\mathbf{f}(\mathbf{X})|}_{\mathbf{X}={\mathbf{X}}^{(0)}}\\ ={\left[\begin{array}{c}\frac{\partial f_1(\mathbf{X})}{\partial x_1}\delta x_1+\frac{\partial f_1(\mathbf{X})}{\partial x_2}\delta x_2+\cdots +\frac{\partial f_1(\mathbf{X})}{\partial x_n}\delta x_n\\ \frac{\partial f_2(\mathbf{X})}{\partial x_1}\delta x_1+\frac{\partial f_2(\mathbf{X})}{\partial x_2}\delta x_2+\cdots +\frac{\partial f_2(\mathbf{X})}{\partial x_n}\delta x_n\\ \frac{\partial f_m(\mathbf{X})}{\partial x_1}\delta x_1+\frac{\partial f_m(\mathbf{X})}{\partial x_2}\delta x_2+\cdots +\frac{\partial f_m(\mathbf{X})}{\partial x_n}\delta x_n\end{array}\right]}_{\mathbf{X}={\mathbf{X}}^{(0)}}={\left[\begin{array}{cccc}\frac{\partial f_1(\mathbf{X})}{\partial x_1}& \frac{\partial f_1(\mathbf{X})}{\partial x_2}& \cdots & \frac{\partial f_1(\mathbf{X})}{\partial x_n}\\ \frac{\partial f_2(\mathbf{X})}{\partial x_1}& \frac{\partial f_2(\mathbf{X})}{\partial x_2}& \cdots & \frac{\partial f_2(\mathbf{X})}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_m(\mathbf{X})}{\partial x_1}& \frac{\partial f_m(\mathbf{X})}{\partial x_2}& \cdots & \frac{\partial f_m(\mathbf{X})}{\partial x_n}\end{array}\right]}^{\delta }{\left[\begin{array}{c}\delta x_1\\ \delta x_2\\ ⋮\\ \delta x_n\end{array}\right]}_{X=X^{(0)}}\\ ={J(\mathbf{f}(\mathbf{X}))\delta \mathbf{X}|}_{X=X^{(0)}}\end{array}$$
其中 $\int J(\mathbf{f}(\mathbf{X}))=\frac{\partial \mathbf{f}(\mathbf{X})}{\partial {\mathbf{X}}^{\mathrm{T}}}$ 可称之为雅各比矩阵，$m$ 列多元函数对 $n$ 行的自变量求一阶导得到的矩阵。

二阶展开项详细表达式：
$$\begin{array}{l}\frac{1}{2}{\left({\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\right)}^2\mathbf{f}\left({\mathbf{X}}^{(0)}\right)={\frac{1}{2}{\left(\frac{\partial }{\partial x_1}\delta x_1+\frac{\partial }{\partial x_2}\delta x_2+\cdots +\frac{\partial }{\partial x_n}\delta x_n\right)}^2\mathbf{f}(\mathbf{X})|}_{X=X^{(0)}}\\ ={\frac{1}{2}\mathrm{tr}\left(\left[\begin{array}{cccc}\frac{{\partial }^2}{\partial x_1^2}& \frac{{\partial }^2}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^2}{\partial x_1\partial x_n}\\ \frac{{\partial }^2}{\partial x_2\partial x_1}& \frac{{\partial }^2}{\partial x_2^2}& \cdots & \frac{{\partial }^2}{\partial x_2\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^2}{\partial x_n\partial x_1}& \frac{{\partial }^2}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^2}{\partial x_n^2}\end{array}\right]\left[\begin{array}{cccc}\delta x_1^2& \delta x_1\delta x_2& \cdots & \delta x_1\delta x_n\\ \delta x_2\delta x_1& \delta x_2^2& \cdots & \delta x_2\delta x_n\\ ⋮& ⋮& \ddots & ⋮\\ \delta x_n\delta x_1& \delta x_n\delta x_2& \cdots & \delta x_n^2\end{array}\right]\right)\mathbf{f}(\mathbf{X})|}_{X={\mathbf{X}}^{(0)}}\\ \begin{array}{l}={\frac{1}{2}\mathrm{tr}\left(\nabla {\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)\mathbf{f}(\mathbf{X})|}_{X=X^{(0)}}={\frac{1}{2}\mathrm{tr}\left(\nabla {\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right){\sum }_{j=1}^m{\mathbf{e}}_j{f}_j(\mathbf{X})|}_{X=X^{(0)}}\\ ={\frac{1}{2}{\sum }_{j=1}^m{\mathbf{e}}_j\mathrm{tr}\left(\nabla {\nabla }^{\mathrm{T}}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)f_j(\mathbf{X})|}_{X=X^{(0)}}=\frac{1}{2}{\sum }_{j=1}^m{\mathbf{e}}_j\mathrm{tr}\left({\nabla {\nabla }^{\mathrm{T}}{f}_j(\mathbf{X})|}_{X=X^{(0)}}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)\end{array}\\ =\frac{1}{2}{\sum }_{j=1}^m{\mathbf{e}}_j\mathrm{tr}(\mathcal{H}\left({f_j(\mathbf{X})|}_{X=X^{(0)}}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)\end{array}$$

$$\mathbf{Y}=\mathbf{f}\left({\mathbf{X}}^{(0)}\right)+J\left(f\left(X^{(0)}\right)\right)\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^m{e}_i\mathrm{tr}\left(\mathcal{H}\left(f_i\left(X^{(0)}\right)\right)\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)+O^3$$

其中 $\mathcal{H}$ 为海森矩阵，$m$ 列多元函数对 $n$ 行的自变量求二阶导得到的矩阵，m 个向量函数有 m 个海森矩阵。

二、扩展Kalman滤波

遇到非线性的状态空间模型时，对状态方程和量测方程做线性化处理，取泰勒展开的一阶项。

状态空间模型(加性噪声，噪声和状态直接是相加的)

这里简单的用加性噪声模型表示，一般形式为 ${\mathbf{X}}_k=\mathbf{f}\left({\mathbf{X}}_{k-1},{\mathbf{W}}_{k-1},k-1\right)$ ，非线性更强，更一般，可以表示噪声和状态之间复杂的关系

$$\{\begin{array}{l}{\mathbf{X}}_k=\mathbf{f}\left({\mathbf{X}}_{k-1}\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\\ {\mathbf{Z}}_k=\mathbf{h}\left({\mathbf{X}}_k\right)+{\mathbf{V}}_k\end{array}$$

选择 $k-1$ 时刻参考值 ${\mathbf{X}}_{k-1}^n$ ，参考点和真实值偏差 $\delta {\mathbf{X}}_{k-1}={\mathbf{X}}_{k-1}-{\mathbf{X}}_{k-1}^n$

状态一步预测：上一时刻参考点带入状态方程 ${\mathbf{X}}_{k/k-1}^n=\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)$ ，预测值的偏差 $\delta {\mathbf{X}}_k={\mathbf{X}}_k-{\mathbf{X}}_{k/k-1}^n$ 。

量测一步预测：${\mathbf{Z}}_{k/k-1}^n=\mathbf{h}\left({\mathbf{X}}_{k/k-1}^n\right)$ ，偏差 $\delta {\mathbf{Z}}_k={\mathbf{Z}}_k-{\mathbf{Z}}_{k/k-1}^n$ 。

展开得状态偏差方程：
$$\begin{array}{ll}& {\mathbf{X}}_k\approx \mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)+\mathbf{J}\left(\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)\right)\left({\mathbf{X}}_{k-1}-{\mathbf{X}}_{k-1}^n\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\\ & {\mathbf{X}}_k-\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)\approx {\mathbf{\Phi }}_{k/k-1}^n\left({\mathbf{X}}_{k-1}-{\mathbf{X}}_{k-1}^n\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\\ & \delta {\mathbf{X}}_k={\mathbf{\Phi }}_{k/k-1}^n\delta {\mathbf{X}}_{k-1}+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\end{array}$$
展开得量测偏差方程：
$$\begin{array}{ll}& {\mathbf{Z}}_k\approx \mathbf{h}\left({\mathbf{X}}_{k/k-1}^n\right)+\mathbf{J}\left(\mathbf{h}\left({\mathbf{X}}_{k/k-1}^n\right)\right)\left({\mathbf{X}}_k-{\mathbf{X}}_{k/k-1}^n\right)+{\mathbf{V}}_k\\ & \delta {\mathbf{Z}}_k={\mathbf{H}}_k^n\delta {\mathbf{X}}_k+{\mathbf{V}}_k\end{array}$$
得偏差状态空间估计模型：
$$\{\begin{array}{l}\delta {\mathbf{X}}_k={\mathbf{\Phi }}_{k\mid k-1}^n\delta {\mathbf{X}}_{k-1}+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\\ \delta {\mathbf{Z}}_k={\mathbf{H}}_k^n\delta {\mathbf{X}}_k+{\mathbf{V}}_k\end{array}$$
偏差量是线性的了，可以用Kalman滤波进行处理：

滤波更新方程：$\delta {\hat{\mathbf{X}}}_k={\mathbf{\Phi }}_{k/k-1}^n\delta {\hat{\mathbf{X}}}_{k-1}+{\mathbf{K}}_k^n\left(\delta {\mathbf{Z}}_k-{\mathbf{H}}_k^n{\mathbf{\Phi }}_{k/k-1}^n\delta {\hat{\mathbf{X}}}_{k-1}\right)$
$$\begin{array}{l}\underset{\delta {\hat{\mathbf{X}}}_{k-1}={\hat{\mathbf{X}}}_{k-1}-{\mathbf{X}}_{k-1}^n}{\underset{\delta {\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_k-{\mathbf{X}}_{k/k-1}^n}{⟶}}{\hat{\mathbf{X}}}_k={\mathbf{X}}_{k/k-1}^n+{\mathbf{K}}_k^n\left({\mathbf{Z}}_k-{\mathbf{Z}}_{k/k-1}^n\right)+\left(\mathbf{I}-{\mathbf{K}}_k^n{\mathbf{H}}_k^n\right){\mathbf{\Phi }}_{k/k-1}^n\left({\hat{\mathbf{X}}}_{k-1}-{\mathbf{X}}_{k-1}^n\right)\\ \stackrel{{\mathbf{X}}_{k-1}^n={\hat{\mathbf{X}}}_{k-1}}{⟶}={\mathbf{X}}_{k/k-1}^n+{\mathbf{K}}_k^n\left({\mathbf{Z}}_k-{\mathbf{Z}}_{k/k-1}^n\right)\end{array}$$
将 $\delta {\hat{\mathbf{X}}}_{k-1}={\hat{\mathbf{X}}}_{k-1}-{\mathbf{X}}_{k-1}^n$ 和 $\delta {\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_k-{\mathbf{X}}_{k/k-1}^n$ 带入得：
$${\hat{\mathbf{X}}}_k={\mathbf{X}}_{k/k-1}^n+{\mathbf{K}}_k^n\left({\mathbf{Z}}_k-{\mathbf{Z}}_{k/k-1}^n\right)+\left(\mathbf{I}-{\mathbf{K}}_k^n{\mathbf{H}}_k^n\right){\mathbf{\Phi }}_{k/k-1}^n\left({\hat{\mathbf{X}}}_{k-1}-{\mathbf{X}}_{k-1}^n\right)$$
此公式就相当于对状态进行操作。前面部分就是Kalman滤波方程。后面多出的粉色部分包含了参考值，令 ${\mathbf{X}}_{k-1}^n={\hat{\mathbf{X}}}_{k-1}$ ，参考点选成上一时刻的估计值，后面一部分就为 $0$ ，得
$${\mathbf{X}}_{k/k-1}^n+{\mathbf{K}}_k^n\left({\mathbf{Z}}_k-{\mathbf{Z}}_{k/k-1}^n\right)$$
EKF滤波公式汇总
$$\{\begin{array}{ll}{\hat{\mathbf{X}}}_{k/k-1}=\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)& \\ {\mathbf{P}}_{k/k-1}={\mathbf{\Phi }}_{k/k-1}{\mathbf{P}}_{k-1}{\mathbf{\Phi }}_{k/k-1}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}& {\mathbf{\Phi }}_{k/k-1}=\mathbf{J}\left(\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)\right)\\ {\mathbf{K}}_k={\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}{\left({\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\right)}^{-1}& {\mathbf{H}}_k=\mathbf{J}\left(\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)\right)\\ {\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_{k/k-1}+{\mathbf{K}}_k\left[{\mathbf{Z}}_k-\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)\right]& \\ {\mathbf{P}}_k=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k/k-1}& \end{array}$$

• 状态转移矩阵是状态方程在 $k-1$ 处的一阶偏导组成的雅可比矩阵。
• 设计矩阵是量测方程在 $k-1$ 处的一阶偏导组成的雅可比矩阵。

三、二阶滤波

状态方程的二阶泰勒展开：

$${\mathbf{X}}_k=\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)+{\mathbf{\Phi }}_{k/k-1}^n\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}^{-}\cdot \mathbf{\delta }\mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}$$
状态预测：上面的方程两边求均值得：
$$\begin{array}{rl}{\hat{\mathbf{X}}}_{k/k-1}& =\mathrm{E}\left[\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)+{\mathbf{\Phi }}_{k/k-1}^n\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\cdot \mathbf{\delta }\mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\right]\\ & =\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)+{\mathbf{\Phi }}_{k/k-1}^n\mathrm{E}[\delta \mathbf{X}]+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\cdot \mathrm{E}\left[\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right]\right)+{\mathbf{\Gamma }}_{k-1}\mathrm{E}\left[{\mathbf{W}}_{k-1}\right]\\ & =\mathbf{f}\left({\mathbf{X}}_{k-1}^n\right)+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}{\mathbf{P}}_{k-1}\right)\end{array}$$
状态预测既和状态的传递有关系，也和方差 $P$ 阵有关系，比较麻烦。

状态预测的误差：
$$\begin{array}{rl}{\tilde{\mathbf{X}}}_{k/k-1}& ={\mathbf{X}}_k-{\hat{\mathbf{X}}}_{k/k-1}\\ & ={\mathbf{\Phi }}_{k/k-1}^n\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}-\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}{\mathbf{P}}_{k-1}\right)\\ & ={\mathbf{\Phi }}_{k/k-1}^n\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\end{array}$$
状态预测的方差：比较复杂，最后算下来和四阶矩有关系
$$\begin{array}{l}{\mathbf{P}}_{k/k-1}=\mathrm{E}\left[{\tilde{\mathbf{X}}}_{k/k-1}{\tilde{\mathbf{X}}}_{k/k-1}^{\mathrm{T}}\right]\\ =\mathrm{E}[\left[{\mathbf{\Phi }}_{k\mid k-1}^n\delta \mathbf{X}+\frac{1}{2}{\sum }_{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\right]\\ \times {\left[{\mathbf{\Phi }}_{klk-1}^n\delta \mathbf{X}+\frac{1}{2}{\sum }_{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\right]}^{\mathrm{T}}]\\ ={\mathbf{\Phi }}_{kk/k-1}^n{\mathbf{P}}_{k-1}{\left({\mathbf{\Phi }}_{k/k-1}^n\right)}^{\mathrm{T}}\\ +\frac{1}{4}\mathrm{E}\left[{\sum }_{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{fi}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right){\left({\sum }_{i=1}^n{\mathbf{e}}_i\mathrm{tr}\left({\mathbf{D}}_{f_i}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)\right)}^{\mathrm{T}}\right]+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}\\ ={\mathbf{\Phi }}_{k/k-1}^n{\mathbf{P}}_{k-1}{\left({\mathbf{\Phi }}_{k/k-1}^n\right)}^{\mathrm{T}}\\ +\frac{1}{4}{\sum }_{i=1}^n{\sum }_{j=1}^n{\mathbf{e}}_i{\mathbf{e}}_j^{\mathrm{T}}\mathrm{E}\left[\mathrm{tr}\left({\mathbf{D}}_{fi}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)\cdot \mathrm{tr}\left({\mathbf{D}}_{jj}\left(\delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}-{\mathbf{P}}_{k-1}\right)\right)\right]+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}\\ ={\mathbf{\Phi }}_{k/k-1}^n{\mathbf{P}}_{k-1}{\left({\mathbf{\Phi }}_{k/k-1}^n\right)}^{\mathrm{T}}+\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\mathbf{e}}_{\mathbf{i}}{\mathbf{e}}_j^{\mathrm{T}}\mathrm{tr}\left({\mathbf{D}}_{fi}{\mathbf{P}}_{k-1}{\mathbf{D}}_{fj}{\mathbf{P}}_{k-1}\right)+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}\end{array}$$
量测方程的二阶展开：
$$Z_{k/k-1}=h\left(X_{k/k-1}^n\right)+{\mathbf{H}}_k^n\delta \mathbf{X}+\frac{1}{2}\sum _{i=1}^m{e}_{i}ir\left(D_{hi}\cdot \delta \mathbf{X}\delta {\mathbf{X}}^{\mathrm{T}}\right)+V_k$$
量测预测：
$${\hat{\mathbf{Z}}}_{k/k-1}=\mathbf{h}\left({\mathbf{X}}_{k/k-1}^n\right)+\frac{1}{2}\sum _{i=1}^m{e}_i\mathrm{tr}\left({\mathbf{D}}_{hi}{\mathbf{P}}_{k/k-1}\right)$$
量测预测方差阵：
$${\mathbf{P}}_{zz,kk-1}={\mathbf{H}}_k^n{\mathbf{P}}_{k/k-1}{\left({\mathbf{H}}_k^n\right)}^{\mathrm{T}}+\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\mathbf{e}}_i^{\mathrm{e}}{\mathrm{e}}_j^{\mathrm{t}}\left({\mathbf{D}}_{hi}{\mathbf{P}}_{k/k-1}{\mathbf{D}}_{hj}{\mathbf{P}}_{k/k-1}\right)+{\mathbf{R}}_k$$
状态/量测互协方差阵：
$${\mathbf{P}}_{xz,kk-1}={\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^n$$
最后，得二阶滤波公式：红色部分是二阶多出来的，运算量巨大收益微小

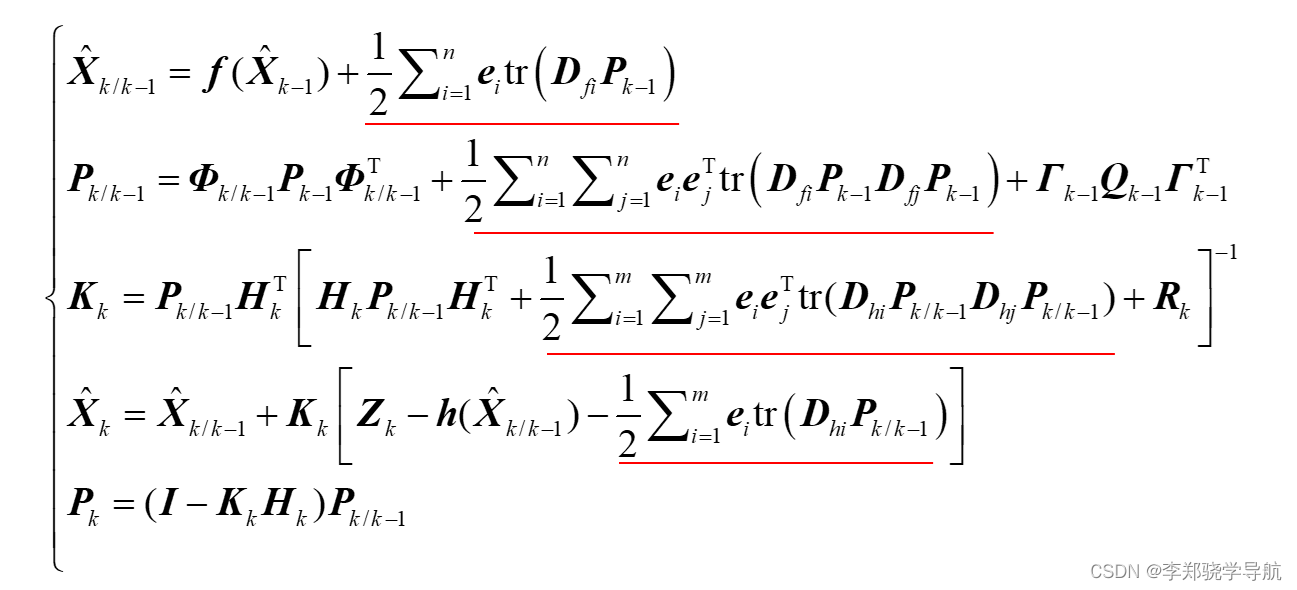
四、迭代EKF滤波

$$\{\begin{array}{ll}{\hat{\mathbf{X}}}_{k/k-1}=\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)& \\ {\mathbf{P}}_{k/k-1}={\mathbf{\Phi }}_{k/k-1}{\mathbf{P}}_{k-1}{\mathbf{\Phi }}_{k/k-1}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}& {\mathbf{\Phi }}_{k/k-1}=\mathbf{J}\left(\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)\right)\\ {\mathbf{K}}_k={\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}{\left({\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\right)}^{-1}& {\mathbf{H}}_k=\mathbf{J}\left(\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)\right)\\ {\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_{k/k-1}+{\mathbf{K}}_k\left[{\mathbf{Z}}_k-\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)\right]& \\ {\mathbf{P}}_k=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k/k-1}& \end{array}$$

非线性系统展开点越接近你想研究的那个点，展开的精度越高。普通EKF的展开点是上一时刻 $k-1$，考虑迭代修正展开点。做完一次滤波之后，有 $k$ 时刻的新量测值，可以用新量测值对 $k-1$ 时刻做反向平滑，用反向平滑的值作为新的上一时刻的状态估计值，进行Kalman滤波。

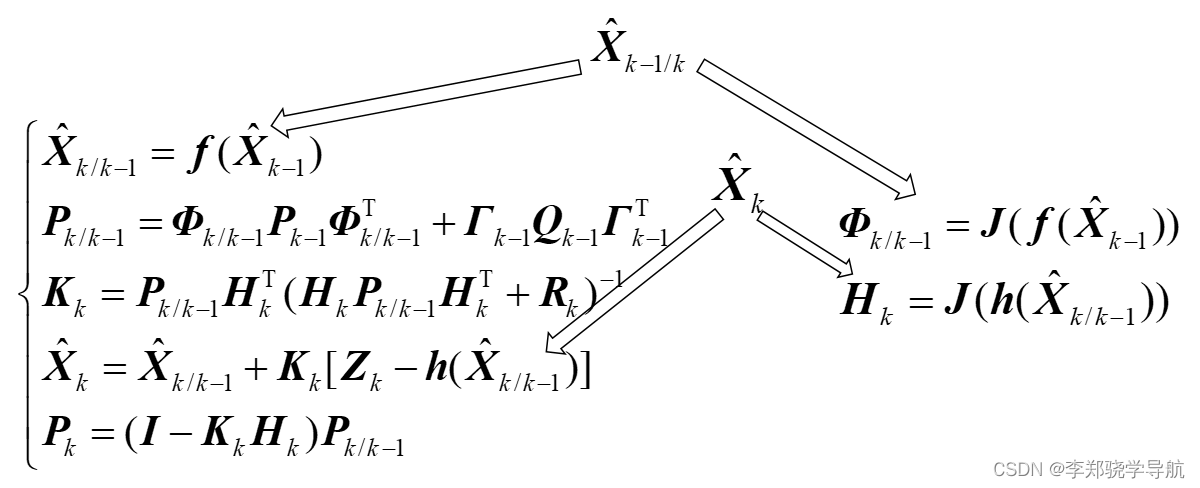
预滤波：
$$\{\begin{array}{ll}{\hat{\mathbf{X}}}_{k/k-1}^{\ast }=\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)& \\ {\mathbf{P}}_{k/k-1}^{\ast }={\mathbf{\Phi }}_{k/k-1}^{\ast }{\mathbf{P}}_{k-1}{\left({\mathbf{\Phi }}_{k/k-1}^{\ast }\right)}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}& {\mathbf{\Phi }}_{k/k-1}^{\ast }=\mathbf{J}\left(\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)\right)\\ {\mathbf{K}}_k^{\ast }={\mathbf{P}}_{k/k-1}^{\ast }{\left({\mathbf{H}}_k^{\ast }\right)}^{\mathrm{T}}{\left[{\mathbf{H}}_k^{\ast }{\mathbf{P}}_{k/k-1}^{\ast }{\left({\mathbf{H}}_k^{\ast }\right)}^{\mathrm{T}}+{\mathbf{R}}_k\right]}^{-1}& {\mathbf{H}}_k^{\ast }=\mathbf{J}\left(\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}^{\ast }\right)\right)\\ {\hat{\mathbf{X}}}_k^{\ast }={\hat{\mathbf{X}}}_{k/k-1}^{\ast }+{\mathbf{K}}_k^{\ast }\left[{\mathbf{Z}}_k-\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}^{\ast }\right)\right]& \end{array}$$
反向一步平滑：可以用RTS算法
$${\hat{\mathbf{X}}}_{k-1/k}={\hat{\mathbf{X}}}_{k-1}+{\mathbf{P}}_{k-1}{\left({\mathbf{\Phi }}_{k/k-1}^{\ast }\right)}^{\mathrm{T}}{\left({\mathbf{P}}_{k/k-1}^{\ast }\right)}^{-1}\left({\hat{\mathbf{X}}}_k^{\ast }-{\hat{\mathbf{X}}}_{k/k-1}^{\ast }\right)$$
重做状态一步预测：${\hat{\mathbf{X}}}_{k-1/k}$ 再做泰勒级数展开
$$\begin{array}{rl}{\hat{\mathbf{X}}}_{k/k-1}& =\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)=\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)+\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1}\right)-\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)\\ & \approx \mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)+\mathbf{J}\left(\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)\right)\left({\hat{\mathbf{X}}}_{k-1}-{\hat{\mathbf{X}}}_{k-1/k}\right)\end{array}$$
重做量测一步预测：
$$\begin{array}{rl}{\hat{\mathbf{Z}}}_{k/k-1}& =\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)=\mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)+\mathbf{h}\left({\hat{\mathbf{X}}}_{k/k-1}\right)-\mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)\\ & \approx \mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)+\mathbf{J}\left(\mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)\right)\left({\hat{\mathbf{X}}}_{k/k-1}-{\hat{\mathbf{X}}}_k^{\ast }\right)\end{array}$$
迭代滤波：在此基础上做Kalman滤波
$$\{\begin{array}{ll}{\hat{\mathbf{X}}}_{k/k-1}=\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)+{\mathbf{\Phi }}_{k/k-1}\left({\hat{\mathbf{X}}}_{k-1}-{\hat{\mathbf{X}}}_{k-1/k}\right)& \\ {\mathbf{P}}_{k/k-1}={\mathbf{\Phi }}_{k/k-1}{\mathbf{P}}_{k-1}{\mathbf{\Phi }}_{k/k-1}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}& {\mathbf{\Phi }}_{k/k-1}=\mathbf{J}\left(\mathbf{f}\left({\hat{\mathbf{X}}}_{k-1/k}\right)\right)\\ {\mathbf{K}}_k={\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}{\left({\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\right)}^{-1}& {\mathbf{H}}_k=\mathbf{J}\left(\mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)\right)\\ {\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_{k/k-1}+{\mathbf{K}}_k\left[{\mathbf{Z}}_k-\mathbf{h}\left({\hat{\mathbf{X}}}_k^{\ast }\right)-{\mathbf{H}}_k\left({\hat{\mathbf{X}}}_{k/k-1}-{\hat{\mathbf{X}}}_k^{\ast }\right)\right]& \\ {\mathbf{P}}_k=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k/k-1}& \end{array}$$

还可以多次迭代，但收益小