论文题目:《Mis-classifified Vector Guided Softmax Loss for Face Recognition》
论文地址:https://arxiv.org/pdf/1912.00833v1.pdf
代码地址:http://www.cbsr.ia.ac.cn/users/xiaobowang/
1.背景
迄今为止,提出了几种基于margin的softmax损失函数(cosface、sphereface、arcface…)用来增加不同类特征的间隔。虽然它们都取得了重要的成就,但是也存在几个问题:
1、没有考虑到特征挖掘的重要性,而且样本挖掘的时候怎么清晰定义难易样本;
2、设置margin时只考虑从Ground Truth 类出发,未从其他类别考虑判别性;
3、设置margin时不同的类都是固定的间隔m值,不适合很多真实场景的情况;
MVface可以自适应地重点关注误分类的特征向量,以此指导判别性特征学习。这也是首次将特征margin的优点和特征挖掘的优点集中在一个统一的损失函数里面。
2.相关工作
为了解决问题1,曾经有人采用基于样本挖掘策略的softmax损失函数(HM-softmax),在mini-batch选取一定比例的高损失的样本来训练,但是这个困难样本的比例往往取决于经验,简单样本则完全丢弃。后来有人设计了一个相对’软’的策略,名为Focal loss(F-softmax),也就是简单样本不用丢弃,只是轻微关注,而重点关注困难样本。然而这些困难样本的定义是不清晰的,所以这两个策略难以提升性能。
- softmax损失函数:
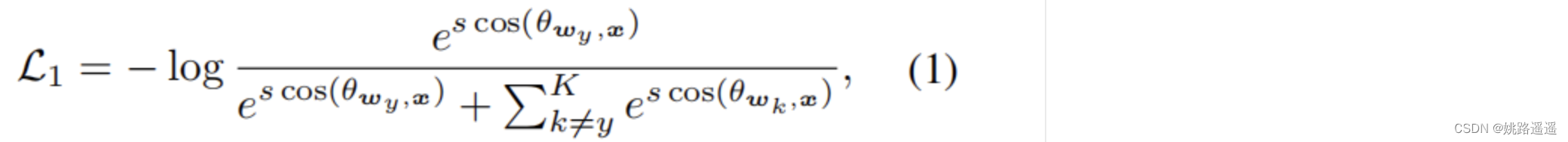
K是类别数,wk权重和特征x经过归一化后被参数s取代 - Mining-based Softmax函数:
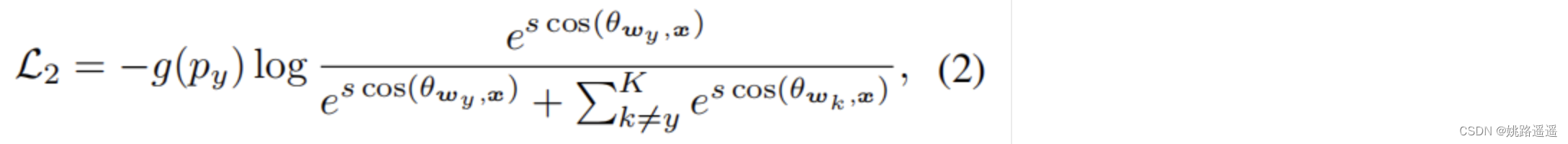
Py是预测的后验概率,g(Py)是一个指示函数
如果是HM-Softmax, g(Py)=1 if sample is hard else 0
如果是F-Softmax, g(Py)=(1-Py)𝛾 - Margin-based Softmax损失函数:
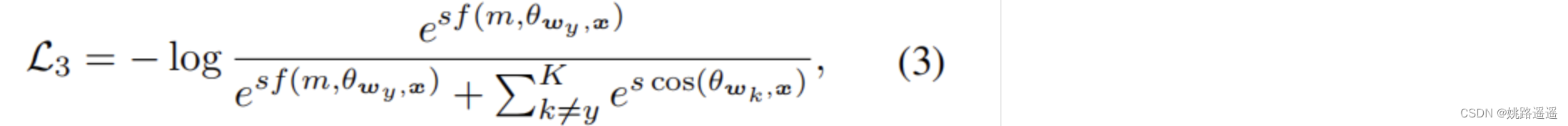
f(m, 𝜃wy, x)是设计的Margin函数,有多种形式,比如A-Softmax,AM-softmax、Arc-Softmax都有不同的设计。甚至还可以将他们混合起来为 f(m,𝜃wy,x)=cos(m1, 𝜃wy, x+m3)-m2 - Naive Mining-Margin Softmax Loss
为了解决问题1,最直接简单的手段将Mining-based 和Margin-based 集中在一起
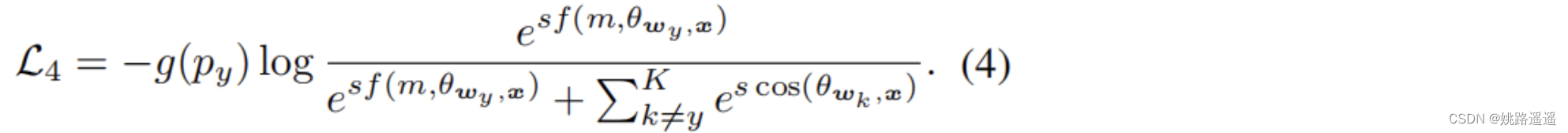
但是在实践中上述函数并没有很好地改进性能,原因可能是HM-Softmax舍弃了部分容易样本,而对于F-Softmax而言,它使用了所有样本,并根据经验通过调整因子对每个样本进行了加权,但是训练中的困难样本定义不清晰,没有直观的解释。
3.MVFace
直觉说,考虑分离良好的特征向量对学习问题影响很小。 这意味着错误分类的特征向量对于增强特征判别性更为关键。论文中定义一个指示器函数动态地指定一个样本是否为误分类,如下:
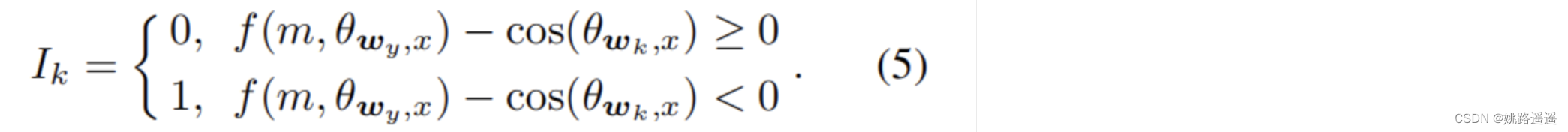
k不等于y,也就是Ik与除了GroundTruth的其他类有关。
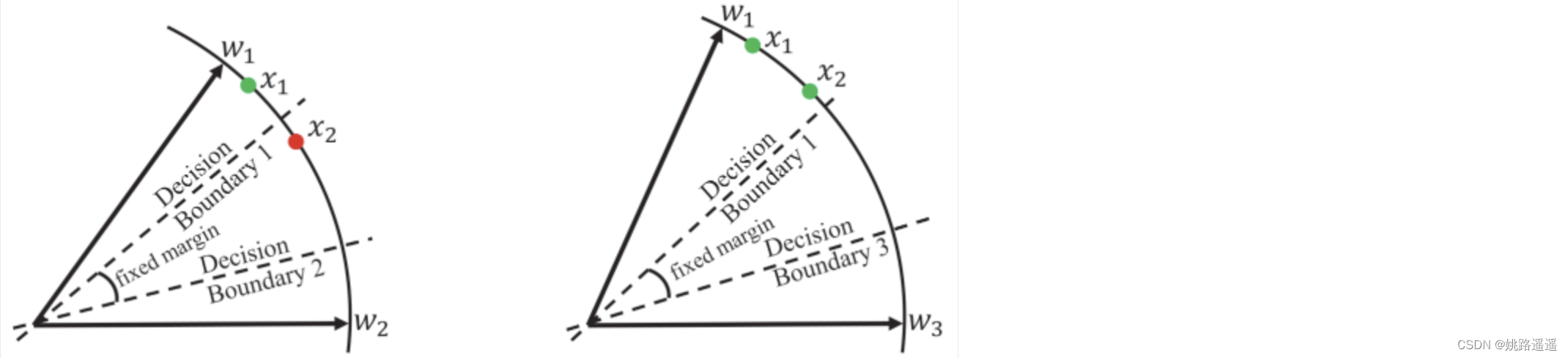
比如看上图的左边部分,特征x2属于类1,但是被误分类了,即f(m, 𝜃w1,x2)-cos(𝜃w2,x2)<0,那么这些样本会暂时被重点对待,用这种方式困难样本就清晰地被指示了。主要是集中这些困难样本的训练,因此制定了MV-Softmax损失函数:
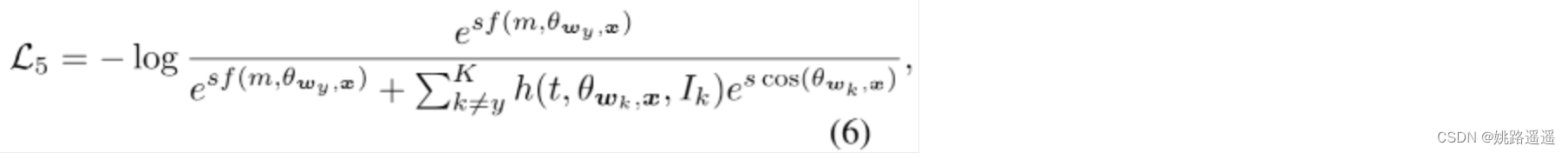
h(t,𝜃wy,x,Ik)是对误分类的样本加权的函数,有两种形式,一个是对所有误分的类固定权重:
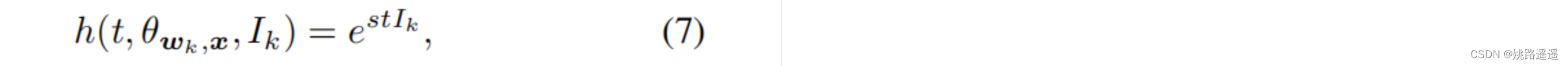
另外一种是自适应动态加权:

t>=0是预设超参数,很明显,如果t=0就成为了Margin-based Softmax损失函数
Empirically set t in [0.2,0.3]
最终损失(自适应):
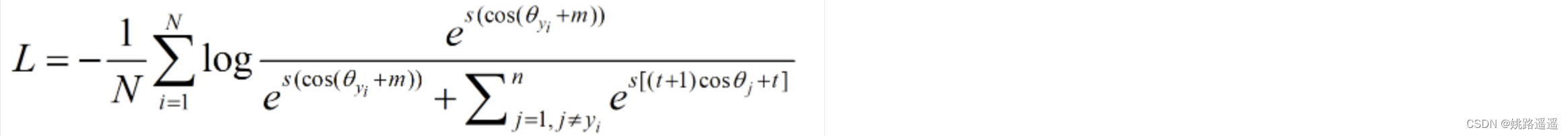
4. 对比
4.1. Comparision to Mining-based Softmax Losses
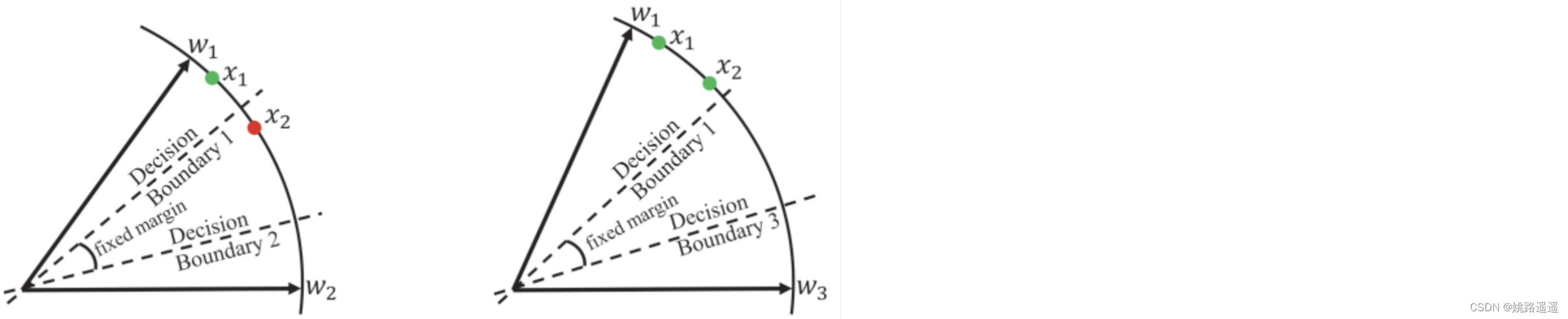
假设两个样本x1和x2 都属于类别1,x1可以很好的分类但x2出现误分类情况。HM-Softmax丢弃了简单样本x1而用困难样本x2训练。F-Softmax并未明确指示困难样本,但会重新加权所有样本,从而使一个较困难的x2具有相对较大的损失值。这两种策略都是直接从损失的角度出发,困难样本的选择没有语义上的指导。本文提出的MV-softmax首先根据决策边界在语义上定义了困难样本,而且是从概率的角度来关注困难样本。由于-log§是单调递减函数,减少误分类向量x2的后验概率将会增加x2在训练中的重要性。总的来说可以看出本文提出的方法对于判别性特征学习更优于先前的方法。
4.2. Comparision to Margin-based Softmax Losses
依然假设样本x2来自于类别1,没有很好的分类。原始的softmax损失目标是使得w1T*x2 > w2Tx2,w1Tx2 > w3Tx3,特征和权重归一化后等价为:cos(𝜃1) > cos(𝜃2),cos(𝜃1) > cos(𝜃3)。为了使上述关系更加严格,基于margin的损失函数引进一个margin函数f(m,𝜃1)=cos(m1𝜃1+m3)-m2,这个margin函数是从GroundTruth类出发,只与𝜃1有关。
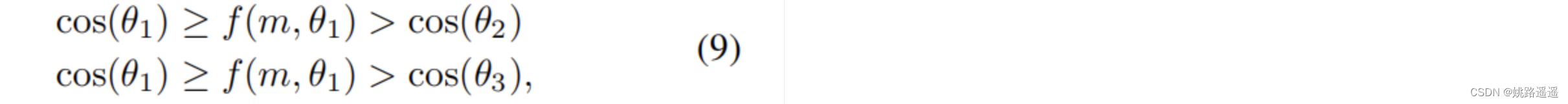
f(m,𝜃1)对于不同的类都是相同固定的,忽视了与其他类的判别性,为了解决这个问题,本文针对误分类的x2引入了与其他类有关的margin函数h*(t,𝜃2)
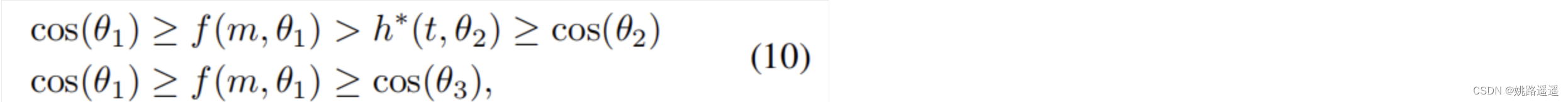
h*(t,𝜃2) = cos(𝜃2) + t (固定形式) or (t + 1)cos(𝜃2) + t (自适应),对于𝜃3而言,由于x2被w3很好的分类,所以不需要加上额外的条件。用MV-AM-Softmax举例 (f(m,𝜃y) = cos(𝜃y) - m),对于误分类的样本,margin为m + t or m + tcos(𝜃2) + t(这个margin是自适应的与cos(𝜃2)有关 )。通过以上的这些改进,MV-Softmax很好地解决了第二和第三个缺点。
5. 算法流程


![[hadoop全分布部署]安装Hadoop、配置Hadoop 配置文件②](https://img-blog.csdnimg.cn/0cbfd041ee58405fb8b9e0b983ace87c.png)