本系列文章主要对Bug类路径规划算法的原理进行介绍,在本系列的第一篇文章中按照时间顺序梳理了自1986年至2018年Bug类路径规划算法的发展,整理了13种BUG系列中的典型算法,从本系列的第二篇文章开始依次详细介绍了其中具有代表性的BUG1、BUG2、Tangent BUG、I-BUG、RandomBug、BugFlood等算法。
本篇文章作为本系列文章第二篇文章,主要对BUG1和BUG2算法进行介绍
本系列其他文章见:BUG系列路径规划算法原理介绍——总结篇
一、BUG1 BUG2算法的提出
1987年 Vladimir J. Lumelsky 和 Alexander A. Stepanov 在论文《Path-planning strategies for a point mobile automaton moving amidst unknown obstacles of arbitrary shape》中回顾了BUG1 算法,并提出了BUG2算法。
(1)论文链接:https://linkspringer.53yu.com/article/10.1007/bf01840369
(2)论文DOI:10.1007/bf01840369
二、BUG1算法
BUG1算法的基本思想是在没有障碍物时,沿着直线向目标运动可以得到最短的路线。当遇到障碍物时,机器人绕行障碍物直到能够继续沿直线项目标运动。即BUG1算法在不断的执行两个行为:向目标直行和绕着障碍物的边界走,直至到达目标点或发现无可行路径。
算法的基本流程是机器人从起点出发,沿着从起点到目标点的直线运动,直至遇到障碍物停止直行行为,开始绕行行为,机器人会沿着障碍物的边界绕行一圈,直至回到开始绕行的位置,然后找到绕行当前障碍物一圈中距离目标点最近的点,并将机器人移动到该点,绕行行为结束,判断从该点到目标点的直线是否与当前障碍物相交,若相交则认为不存在目标点的路径,结束规划,若不相交,则继续从该点开始继续朝目标点执行直行行为,如此循环直至到达目标点或发现无可行路径退出规划。
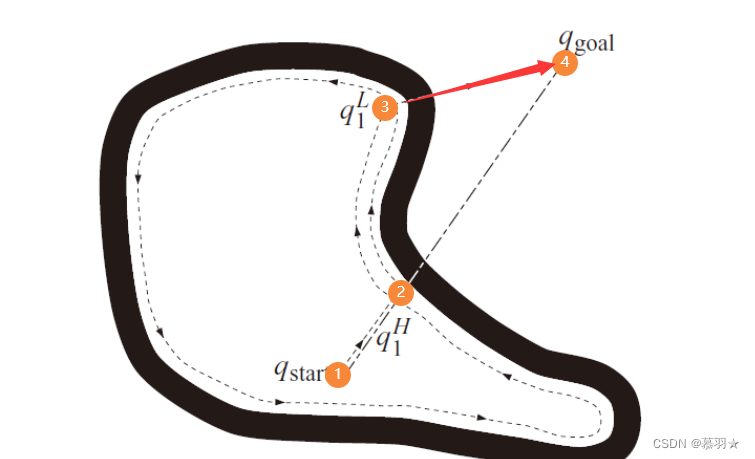
上述中遇到障碍物开始绕行的点称为撞击点,结束绕行继续朝目标点直行移动的点称为离开点。以下图的例子中,机器人从①处出发,沿着直线①–⑥的方向移动,直至到达撞击点②处,从②处开始执行绕行行为,绕着当前障碍物运动一圈回到②处,并判断出绕行过程中距离目标点⑥处最近的点③,机器人从②处移动到离开点③处,判断直线③–⑥是否与当前障碍物相交,本例中不相交,机器人开始沿着直线③–⑥运动,此时机器人以成功绕过了第一个障碍物WO1,以此类推绕过WO2,到达目标点。
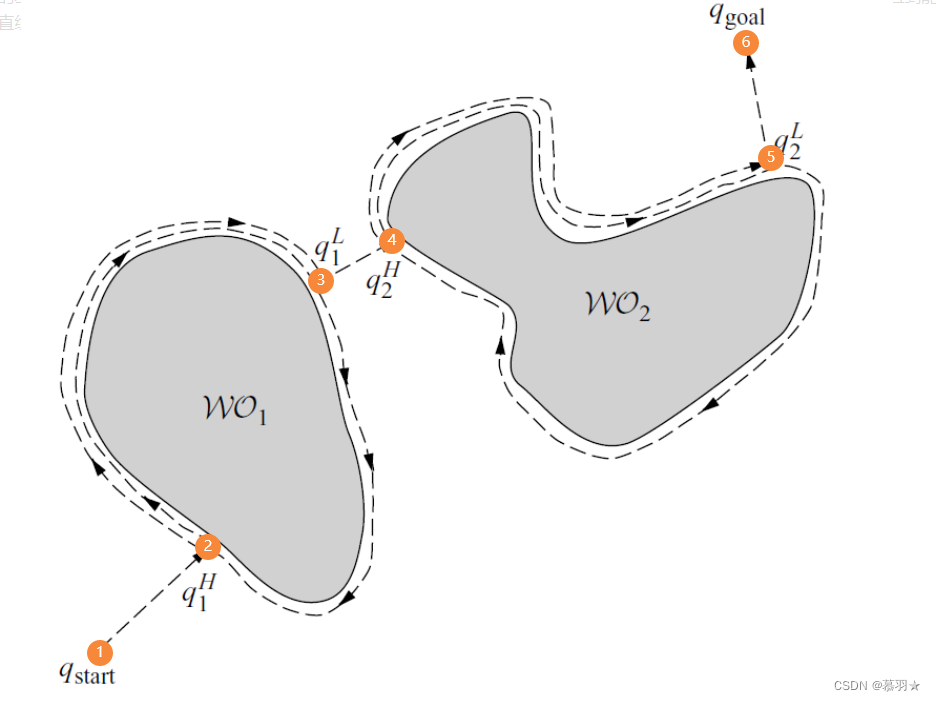
在下面的例子中,机器人在离开点③处,发现③到目标点④的直线与当前障碍物相交,即认为不存在从起始点①到目标点④的可行路径。
BUG1算法的伪代码如下:

总的来说,BUG1算法采用了一种比较保守的策略,效率很低,但可以保证机器人能到达任何可达的目标。
三、BUG2算法
BUG2算法也包含朝向目标的直行和沿边界绕行两种运动。与BUG1算法不同的是,BUG2算法中的直行运动始终是沿着从起点到目标点的直线方向进行的,并且BUG2算法在遇到障碍物时不再采用绕行一圈再判断距离目标点最近的离开点的策略,而是改用以下策略:
当机器人沿着从起始点到目标点方向执行直线运动的过程中遇到障碍物时,机器人开始绕行障碍物,如果机器人在绕行过程中在距离目标更近的点与从起始点到目标点方向的直线相交,并且此时从此处朝着目标点移动暂时不会碰到障碍物时,就停止绕行,继续沿着该直线向目标直行,若不满足以上条件就继续绕行,直至找到满足条件的点停止绕行,转而执行直行运动,若一种不满足,机器人回到了开始绕行的点,那么此时便认为机器人不能到达目标点。
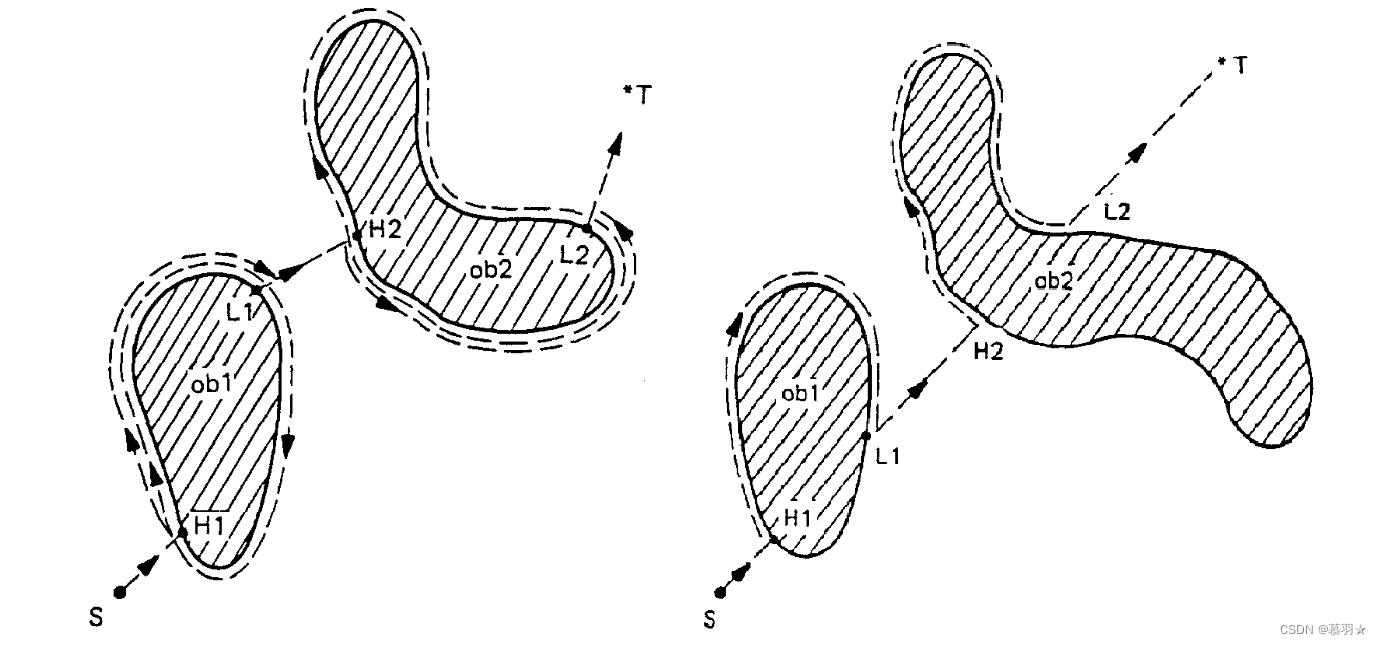
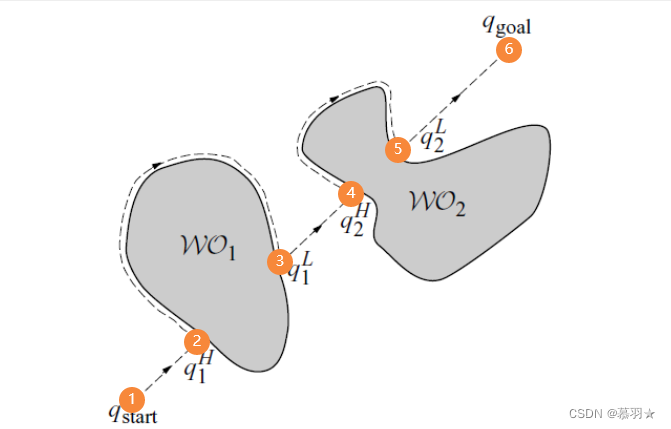
比如在下面的例子中,机器人从①处出发沿着①–⑥的方向执行直线运动,直至在②处遇到障碍物,开始执行绕行运动,绕行到③处后重新与直线①–⑥相交,并且③处比开始绕行的②处距离目标点更近,则在③处停止绕行,并继续从③处沿着直线①–⑥的方向执行直线运动,以此类推,最终达到目标点⑥处。
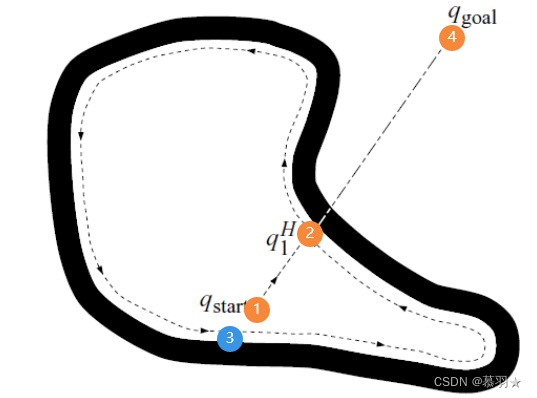
再比如在下面的例子中,机器人从①处出发沿着①–④的方向执行直线运动,直至在②处遇到障碍物,开始执行绕行运动,绕行到③处后重新与直线①–⑥相交,但是经过判断发现相比于开始绕行的②处,③处离目标点④更远,因此继续绕行,绕行到②处重新与直线①–⑥相交,发现回到了开始绕行的地方,此时认为没有从起点①到目标点④的路径,退出规划。
现在总结一下,在某点处停止绕行运动,转而执行直行运动,需要满足以下5个条件:
(1)没有达到目标点 (若在绕行过程中,恰好到达了目标点,则规划完成,不需要再执行直行运动)
(2)该点与由起始点和目标点所确定的直线相交,或者说该点在由起始点和目标点所确定的直线上
(3)没有回到开始绕行的点
(4)从该点处朝着目标点执行直线运动暂时不会遇到障碍物
(5)相比于开始绕行的点,该点距离目标点更近
以上条件可按照(1)~ (5)的顺序进行判断,且只有在满足(1)和(2)的情况下,才需要进行(3)~(5)的判断。
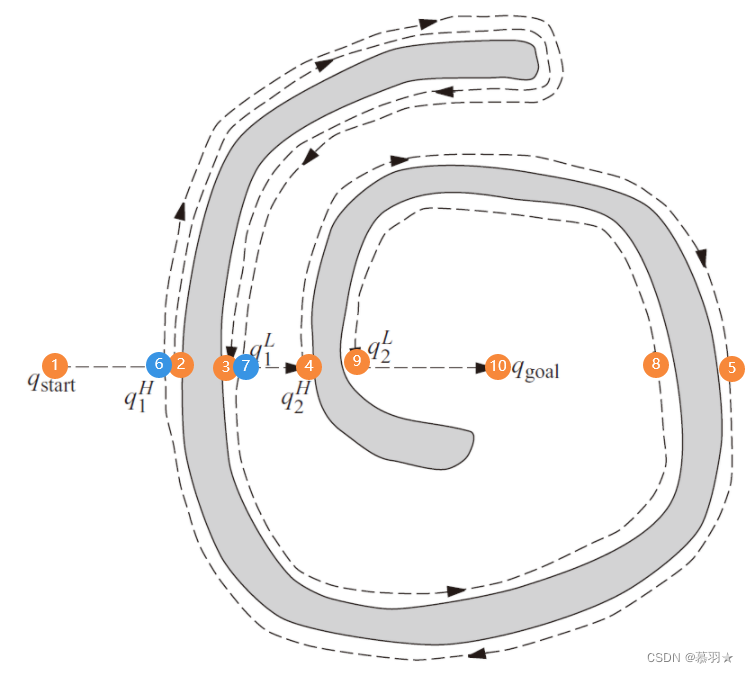
在如下面的例子所示的环境中,算法的效率会变得很低,机器人从①处出发沿着由起始点①和目标点⑩确定的直线①–⑩执行直行运动,到达②处,开始绕行,绕行到③处,满足以上5个停止绕行的条件,结束绕行,转而执行直行运动到达④处,再次开始绕行,绕行到⑤处,依次判断以上5个条件,不满足条件(4),因此继续绕行到⑥处(即②处),不满足条件(4),继续绕行到⑦处(即③处),不满足条件(5),继续绕行到⑧处,若⑧处比开始绕行的④处离目标点⑩处更近,则⑧处满足以上5个条件,由⑧处朝着⑩处直行运动达到目标点结束规划,下图的例子中认为⑧处比④处距离⑩处远,即不满足条件(5),继续绕行到⑨处,满足5个条件,结束绕行,从由⑨处朝着⑩处直行运动达到目标点,结束规划。
BUG2算法的伪代码如下:

总的来说,相比于BUG1算法,BUG2算法采用了一种更贪心的策略,部分情况下效率会比BUG1要高一点。
随着环境的复杂性增加(环境中障碍物数量增加),BUG1搜索效率越来越有可能胜过BUG2。BUG1采用详尽的搜索以找到最优的离开点 。BUG2采用贪心搜索,选择找到的第一个有希望的离开点 ,但不能保证最优。当障碍很简单时,BUG2 的贪心搜索会很快获得回报,但是当障碍很复杂时,BUG1更保守的方法通常会产生更好的性能。