1. 引言

前序博客有：

• ECDSA VS Schnorr signature VS BLS signature 第3节“BLS签名”

私钥$pk$，对应的公钥为$P=pk\times G$。待签名消息$m$。
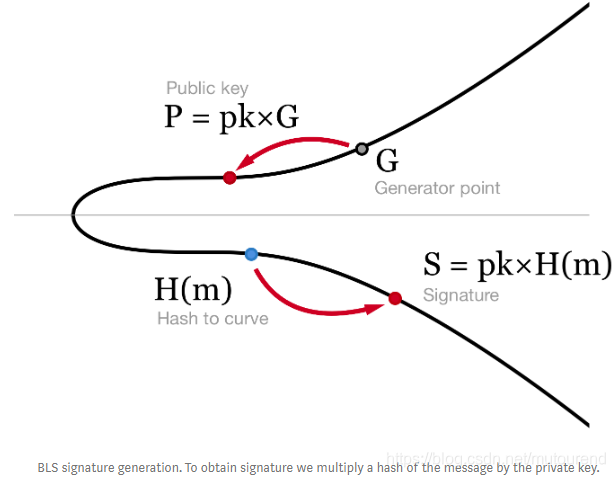
BLS signature的签名流程为：

• 1）通过$H(m)$将消息$m$映射为point on the curve，$G_m=H(m)$。
• 2）将私钥与$H(m)$相乘，$S=pk\times H(m)$，$S$即为相应的签名。

BLS signature is just one single point on the curve that takes only 33bytes in compressed serialization format。
具体如下图示意：

BLS的验签流程为：

• 1）通过$H(m)$将消息$m$映射为point on the curve，$G_m=H(m)$。
• 2）验证$e(P,H(m))=e(G,S)$成立即可。

具有pairing属性，以上验签等式恒成立：
$e(P,H(m))=e(pk\times G,H(m))=e(G,pk\times H(m))=e(G,S)$
具体如下图示意：

整个BLS signature非常简洁优美。

整个BLS签名算法中，有两个关键点是：

• 1）Hashing to the curve：
  ECDSA和Schnorr 签名过程中，需要使用hash函数将消息$m$映射为a number。
  而BLS signature中需要调整hash算法，将消息$m$ hashes directly to the elliptic curve。
  最简单的方式是，仍然将消息$m$通过hash函数映射为a number，然后将该number作为elliptic curve 上point的x坐标。
  Elliptic curves通常有$2^{256}$个points，采用SHA-256 算法可以生成256-bit result。
  但是对于$y^2=x^3+ax+b$形式的eclliptic curve，相同的x坐标，存在$(x,y)和(x,-y)$两个point均在curve上的情况。这就意味着借助SHA-256有约50%的概率能找到two points for some $x$，有50%的概率找到point on the curve。
  
  为了保证对任意的消息$m$均能hashing to the curve，可以在消息$m$后面追加数字，依次尝试直到能找到相应的curve point。如若$hash(m||0)$不能find a point，则依次试$hash(m||1),hash(m||2)$，直到找到point on the curve。【对于$(x,y)和(x,-y)$两个point，实际选择y坐标值更小的那个point。】（如上图所示）

• 2）curve pairing
  BLS signautre要求能够将（相同或者不同）curve上的P和Q两个点映射a number：
  $e(P,Q)\mapsto n$
  同时，应满足如下属性：（使得secret number $x$ unreveal。）
  $e(x\times P,Q)=e(P,x\times Q)$
  更通用的表达为应具有如下属性：
  $e(a\times P,b\times Q)=e(P,ab\times Q)=e(ab\times P,Q)=e(P,Q{)}^{(ab)}$

Hashing to curve函数$H$需为：

• indifferentiable from a random oracle
• 且为constant-time的

令${\mathbb{F}}_q$为某有限域，$E_b:y^2=x^3+b$为某ordinary椭圆曲线（即，non-supersingular椭圆曲线），其$j$-invariant为0，同时满足$\sqrt{b}\in {\mathbb{F}}_q$以及$q\not\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}27)$。
当前最快的constant-time indifferentiable hashing to $E_b({\mathbb{F}}_q)$算法需要：

• 基于${\mathbb{F}}_q$的2次exponentiation运算【以BLS12-377为例，其基于highly 2-adic有限域，相应的indifferentiable Wahby-Boneh hash函数需要应用2次 slow Tonelli-Shanks algorithm算法来提取基域的2个平方根。】

在Dmitrii Koshelev 2021年论文 Indifferentiable hashing to ordinary elliptic ${\mathbb{F}}_q$-curves of $j=0$ with the cost of one exponentiation in ${\mathbb{F}}_q$ 论文中，所实现的constant-time indifferentiable hashing to $E_b({\mathbb{F}}_q)$算法：

• 仅需要1次exponentiation运算。【仍以BLS12-377为例，仅需要提取1次立方根，可 以有限域内的1次exponentiation运算来表示。】

开源实现见：

• https://github.com/dishport/Indifferentiable-hashing-to-ordinary-elliptic-curves-of-j-0-with-the-cost-of-one-exponentiation（Sage脚本）
• https://github.com/zhenfeizhang/indifferentiable-hashing（Rust，但非constant-time实现）