KNN 算法
1. 题目介绍
K近邻(K-Nearest Neighbor, KNN)是一种最经典和最简单的有监督学习方法之一。K-近邻算法是最简单的分类器,没有显式的学习过程或训练过程,是懒惰学习(Lazy Learning)。当对数据的分布只有很少或者没有任何先验知识时,K 近邻算法是一个不错的选择。
从背景上来说,KNN 并不复杂,本文不介绍 KNN 的原理,重点关注如何使用 KNN 来实现手写数字的识别。具体来说,本文使用两种办法来实现 KNN,第一种是使用 numpy 手动实现该算法,第二种是使用 sklearn 中封装好的 KNN 接口,并会简要比较一下两种办法。
本文使用的数据集采用文本文件,每一个文件使用大小为 32 × 32 32×32 32×32 的 0-1 阵列来表示一个手写数字。我们的目标是输入一张这样的图片,然后返回对该图片的预测值。例如下面的几张图片都表示手写数字 ‘0’:
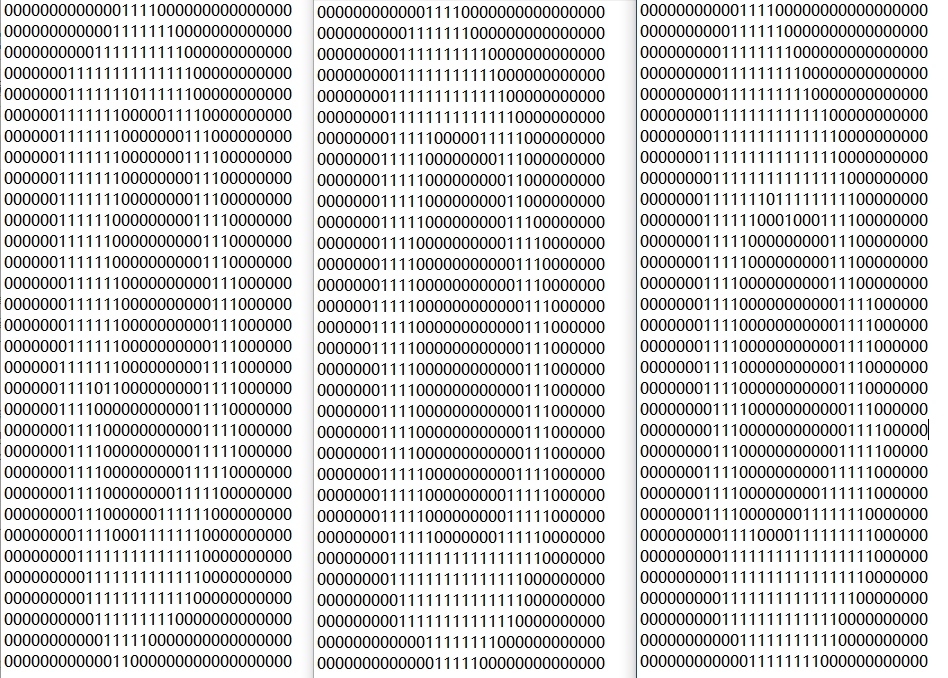
点击链接下载数据集 (有效期至 2023/12/5,过期请留言更新)
2. 代码编排
本实验使用 jupyter 完成,下面按照 cell 的顺序进行介绍。点击下载可执行文件
2.1 全局定义
首先是导入整个项目需要使用到的库,并且定义一些全局变量。training_dir 和 test_dir 分别是训练集和测试集的目录地址,虽然 KNN 中严格来说不存在“训练”和“测试”的概念,但此处把“训练集”理解作空间中已有的那些点,“测试集”就是输入的待分类的点:
import os
import numpy as np
import operator
from sklearn.neighbors import KNeighborsClassifier as kNN
import time
training_dir = 'data/knn-digits/training_digits'
test_dir = 'data/knn-digits/test_digits'
k_global = 3
然后定义对数据集的处理方法。每个文件是 32 × 32 32×32 32×32 的 0-1 阵列,所以我们把他转化为 1 × 1024 1×1024 1×1024 的单行数据,再将单个的数据全部拼接在一起;训练集中一共有 1934 个文件,则最终得到的训练集的大小为 1934 × 1024 1934×1024 1934×1024。
对于测试集,也采用和训练集很类似的方法,但我们希望每提取到一个文件,就对它跑一遍 KNN 算法,以此提高程序的并发度,这里使用了 yield 方法。
# 将32*32的数据转为1*1024的数据
def img2vector(filename):
return_vector = np.zeros((1, 1024))
f = open(filename)
for i in range(32):
line = f.readline()
for j in range(32):
return_vector[0, 32 * i + j] = int(line[j])
return return_vector
def load_training_data():
training_label = []
training_file_list = os.listdir(training_dir)
training_size = len(training_file_list)
training_data = np.zeros((training_size, 1024))
for i in range(training_size):
filename = training_file_list[i]
label = int(filename.split('_')[0])
training_label.append(label)
training_data[i, :] = img2vector(training_dir + '/' + filename)
return training_data, training_label
def load_test_data():
test_file_list = os.listdir(test_dir)
test_size = len(test_file_list)
for i in range(test_size):
filename = test_file_list[i]
label = int(filename.split('_')[0])
test_data = img2vector(test_dir + '/' + filename)
yield test_data, label
2.2 使用 numpy 实现 KNN
我们使用两个函数配合来实现 KNN 算法。第一个函数 classify0 用来对单条数据进行分类,它计算测试点 (shape=(1, 1024)) 与训练数据 (shape=(1934, 1024)) 中每一个点分别的欧式距离,得到一个 1934 大小的一维数组,再从其中挑选 k_global 条距离最近的训练点,将这些点的标签作为 KNN 做出决策的标准。
# 对单条数据进行分类
def classify0(in_data, data_set, labels, k):
data_size = data_set.shape[0]
diff_mat = np.tile(in_data, (data_size, 1)) - data_set
distances = (diff_mat ** 2).sum(axis=1) ** 0.5
argsort_distances = distances.argsort()
class_count = {}
for i in range(k):
label = labels[argsort_distances[i]]
class_count[label] = class_count.get(label, 0) + 1
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
# knn的总体流程
def knn():
error_count = 0
correct_count = 0
training_data, training_label = load_training_data()
for test_data, test_label in load_test_data():
pred_label = classify0(test_data, training_data, training_label, k_global)
if pred_label == test_label:
correct_count += 1
else:
error_count += 1
num_test = error_count + correct_count
acc = correct_count / (correct_count + error_count)
print('test number: %d, failure number: %d, accuracy: %.6f' % (num_test, error_count, acc))
下面执行上述的 knn 函数,并记录它所花费的时间:
time_begin = time.time()
print('use knn implementing from scratch:')
knn()
time_end = time.time()
print('took %f.4 s' % (time_end - time_begin))
程序输出为:

可以看到,一共测试了 946 张图片,仅有 10 张分类错误了,正确率高达 98.94%,效果还是非常不错的。但是它花费了 14.66s,这个时间相比于 sklearn 中现成的接口还是稍显慢的。
2.3 使用 sklearn 实现 KNN
总的来说,sklearn 中的 knn 接口主要就是替代了上文中的 classify0 函数,主体的逻辑流程和之前手动实现的 knn 函数还是很类似的:
def knn_sklearn(algorithm):
error_count = 0
correct_count = 0
training_data, training_label = load_training_data()
classifier = kNN(n_neighbors=k_global, algorithm=algorithm)
classifier.fit(training_data, training_label)
for test_data, test_label in load_test_data():
pred_label = classifier.predict(test_data)
if pred_label == test_label:
correct_count += 1
else:
error_count += 1
num_test = error_count + correct_count
acc = correct_count / (correct_count + error_count)
print('test number: %d, failure number: %d, accuracy: %.6f' % (num_test, error_count, acc))
kNN 函数中有一个参数 algorithm,这个参数决定快速 k 近邻搜索算法,默认为 auto,可以理解为算法自己决定合适的搜索算法。除此之外,可取的值有 kd_tree、ball_tree、brute。
其中,kd_tree 参数构造 kd 树存储数据以便对其进行快速检索的树形数据结构,kd 树也就是数据结构中的二叉树,以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高;ball_tree是为了克服 kd 树高纬失效而发明的,其构造过程是以质心 C 和半径 r 分割样本空间,每个节点是一个超球体;brute 是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。
下面分别演示这四个参数对程序性能的影响:
① auto:
time_begin = time.time()
print('use knn from sklearn:')
knn_sklearn(algorithm='auto')
time_end = time.time()
print('took %f.4 s' % (time_end - time_begin))
输出结果为:
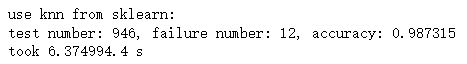
② brute:
time_begin = time.time()
print('use knn from sklearn:')
knn_sklearn(algorithm='brute')
time_end = time.time()
print('took %f.4 s' % (time_end - time_begin))
输出结果为:
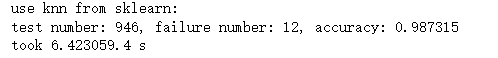
③ kd_tree:
time_begin = time.time()
print('use knn from sklearn:')
knn_sklearn(algorithm='kd_tree')
time_end = time.time()
print('took %f.4 s' % (time_end - time_begin))
输出结果为:
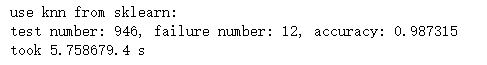
④ ball_tree:
time_begin = time.time()
print('use knn from sklearn:')
knn_sklearn(algorithm='ball_tree')
time_end = time.time()
print('took %f.4 s' % (time_end - time_begin))
输出结果为:
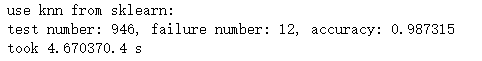
3. 结果分析
基于上述的代码,在不同的 k_global 值下分别测试了 numpy 实现的 KNN、sklearn 中的 KNN (algorithm=‘auto’) 的性能,得到的表格如下:
| k_global | numpy实现的KNN | sklearn中实现的KNN |
|---|---|---|
| 1 | t=14.86s, acc=98.73% | t=6.40s, acc=98.63% |
| 3 | t=14.79s, acc=98.94% | t=8.43s, acc=98.73% |
| 5 | t=14.35s, acc=98.20% | t=7.55s, acc=98.10% |
| 10 | t=14.59s, acc=98.89% | t=6.63s, acc=97.57% |
| 20 | t=14.73s, acc=97.15% | t=6.47s, acc=96.83% |
从上面的表格可以得到几个基本的结论:① k_global 的值不能过大也不能过小,在本实验中,该值为 3 时可以取得较高的精度;② 随着 k_global 的增大,模型所消耗的时间差异并不大,所以不用为了节省时间而选择一个较小的 k_global;③ 使用 numpy 实现的 KNN 耗时总是远高于 sklearn 中的 KNN,但前者的精度只是略高于后者,实际的项目中要根据数据集大小来在时间和精度中取一个 trade-off。
在 k_global = 3 的前提下,比较 sklearn 中的 KNN 在不同 algorithm 参数下的性能,得到下面的表格:
| algorithm | time | acc |
|---|---|---|
| auto | 6.52s | 98.73% |
| brute | 6.48s | 98.73% |
| kd_tree | 5.83s | 98.73% |
| ball_tree | 4.71s | 98.73% |
观察上表,结合上文对 algorithm 参数的介绍,可以得到一个基本的结论:在本实验中,由于样本量并不多,ball_tree 可以使算法用时最少,而 brute 使算法耗时最大(因为它是线性扫描的);默认情况下,auto 参数选择的可能是 brute 参数,因为它们非常接近。
![[附源码]JAVA毕业设计律师事务所网站(系统+LW)](https://img-blog.csdnimg.cn/8403344456ae4ffbbe538c1716c6c7dd.png)