一、数据集背景

乳腺癌数据集是由加州大学欧文分校维护的 UCI 机器学习存储库。
数据集包含 569 个恶性和良性肿瘤细胞样本。
样本类别分布：良性357，恶性212
数据集中的前两列分别存储样本的唯一 ID 编号和相应的诊断（M=恶性，B=良性）。
第 3-32 列包含 30 个实值特征，这些特征是根据细胞核的数字化图像计算得出的，可用于构建模型来预测肿瘤是良性还是恶性。
- 1= 恶性（癌性）- （M）
- 0 = 良性（非癌性）- (B)

为每个样本计算十个实值特征：

半径（从中心到周边点的平均距离）
纹理（灰度值的标准偏差）
周长
面积
平滑度（半径长度的局部变化）
紧凑性（周长^2/面积 - 1.0）
凹度（轮廓凹入部分的严重程度）
凹点（轮廓凹入部分的数量）
对称
分形维数

为每张图像计算这些特征的平均值、标准误差和“最差”或最大（三个最大值的平均值），从而产生 30 个特征。在本实例中我们仅以特征平均值为对象进行研究。

接下来导入库文件，主要包括机器学习库Sklearn中的一些模块

数据清洗和样本显示

根据实例研究的对象指标，输出部分样本的指标分布特征，如下图所示

剔除其他指标仅保留研究对象半径周长和面积平均值指标结果如下

对病人诊断结果进行分类

目标数据进行归类:

恶性肿瘤 - 1
良性肿瘤 - 0

绘制各半径周长面积指标之间的相关关系如下图

选择相关性不小于68%作为阈值，分析特征值与罹患恶性肿瘤的关系结果如下图

将数据划分为自变量和因变量为后续模型分析准备数据

模型分析

下面使用不同分类方式获得分析结果并比较分析精度

可见随机森林法和逻辑回归法的精确度较高效果较好

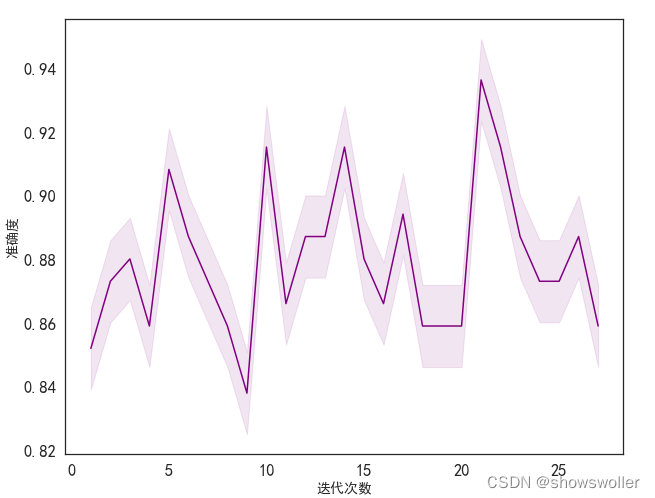
梯度模型准确性变化趋势分析

选择梯度模型分析其在迭代过程中的准确性变化规律

由下图可见第二十一次迭代时达到极值图形阴影部分表示置信区间

二、代码

部分代码如下 需要源码和数据集请点赞关注收藏后评论区留言私信~~~



#导入库

import matplotlib
import matplotlib.pyplot as plt 
import seaborn as sn 
from sklearn.svm import SVC
import numpy as np
import pandas as pds 
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
import xgboost as xgb
from matplotlib import font_manager
from sklearn.neighbors import LocalOutlierFactor
from sklearn.model_selection import train_test_split
#from sklearn.neighbors import NeighborhoodComponentsAnalysis

fontP = font_manager.FontProperties()
fontP.set_family('SimHei')
fontP.set_size(14)


# In[2]:


# 加载数据
dr = pds.read_csv('./data/data.csv')


# In[3]:


dr.head(5)


# In[4]:


dr.info()


# In[5]:


#dr.drop(['id','Unnamed: 32','fractal_dimension_worst','symmetry_worst','concave points_worst','concavity_worst','compactness_worst','smoothness_worst','area_worst','perimeter_worst','texture_worst','radius_worst','fractal_dimension_se','symmetry_se','concave points_se','concavity_se','compactness_se','smoothness_se','area_se','perimeter_se','texture_se','radius_se','radius_se'], axis = 1 , inplace=True)
dr.drop(['id','Unnamed: 32','texture_mean','smoothness_mean','compactness_mean','concavity_mean','concave points_mean','symmetry_mean','fractal_dimension_mean','fractal_dimension_worst','symmetry_worst','concave points_worst','concavity_worst','compactness_worst','smoothness_worst','area_worst','perimeter_worst','texture_worst','radius_worst','fractal_dimension_se','symmetry_se','concave points_se','concavity_se','compactness_se','smoothness_se','area_se','perimeter_se','texture_se','radius_se','radius_se'], axis = 1 , inplace=True)



dr.info()


# In[6]:


dr.diagnosis.replace({"B":0,"M":1},inplace=True)


# **目标数据进行归类:**
# 
# * 恶性肿瘤 - 1
# * 良性肿瘤 - 0

# In[7]:


correlation = dr.corr()
plt.figure(figsize=(7,7))
sn.set(font_scale=1.2)
sn.set(font='SimHei')
sn.heatmap(correlation, cmap='Purples',annot = True,annot_kws={"size": 12}, linewidths=0, linecolor='white', cbar=True, cbar_kws=None, cbar_ax=None, square=False)


# In[8]:


sn.heatmap(correlation, cmap='Purples', xticklabels=['诊断结果', '半径均值', '周长均值', '面积均值'],yticklabels=['诊断结果','半径均值','周长均值', '面积均值'],annot = True,annot_kws={"size": 10}, linewidths=0, linecolor='white', cbar=True, cbar_kws=None, cbar_ax=None, square=False)


# In[9]:


correlation[abs(correlation['diagnosis']) > 0.68].index


# In[10]:


dr.drop('diagnosis', axis=1).corrwith(dr.diagnosis).plot(kind='bar', grid=True, figsize=(6, 6), title="Correlation",color="purple");


# **相关性** 
# * 选择相关性不小于68%作为阈值，分析特征值与罹患恶性肿瘤的关系.
# 

# In[11]:


correlation = dr.corr()
cancer_threshold = 0.68 
filter = np.abs(correlation["diagnosis"]) >= cancer_threshold
correlation.filter = correlation.columns[filter].tolist()
sn.set(font_scale=5.5)
sn.set(font='SimHei')
#sn.clustermap(dr[cf].corr(), figsize=(6, 6), xticklabels=['诊断结果', '面积均值','半径均值', '周长均值'],yticklabels=['周长均值', '半径均值', '面积均值', '诊断结果'],annot = True, annot_kws={"size": 12},cmap="Purples").fig.suptitle("罹患肿瘤相关性分析", fontproperties=fontP,x=0.6, y=1.0) 
res=sn.clustermap(dr.corr(), figsize=(6, 6),annot = True, annot_kws={"size": 16},cmap="Purples").fig.suptitle("罹患肿瘤相关性分析", fontproperties=fontP,x=0.6, y=1.0) 


# In[ ]:





# In[12]:


#组图
sn.set(font_scale=1.5)
sn.set_style(style='white')
sn.pairplot(dr[correlation.filter],dropna=True,grid_kws=None,  diag_kind = "kde", markers = ".", hue = "diagnosis", palette='Purples')


# **去除异常节点** 

# In[13]:


from sklearn.neighbors import LocalOutlierFactor
# 将数据划分为自变量和因变量
y=dr["diagnosis"]
x=dr.drop(["diagnosis"],axis=1)


# In[14]:


# -1代表异常节点
outlier= LocalOutlierFactor()
y.predict=outlier.fit_predict(x)
y.predict[0:10]


# In[15]:


x_factor= outlier.negative_outlier_factor_
pds.dataframe= pds.DataFrame()
pds.dataframe["score"]=x_factor

threshold= -2.5
data_filter= pds.dataframe["score"]< threshold
pds_filter_tolist= pds.dataframe[data_filter].index.tolist()


# In[17]:


x= x.drop(pds_filter_tolist)
y= y.drop(pds_filter_tolist).values


# In[18]:


x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=42)

scaler = StandardScaler()
x_nsform(x_test)


# In[19]:


index = ['梯度法','逻辑回归法','近邻法','支持向量机法','决策树法','随机森林法']
model_list = [GradientBoostingClassifier(),LogisticRegression(), KNeighborsClassifier(n_neighbors = 4), SVC(kernel="rbf"), DecisionTreeClassifier(), RandomForestClassifier(n_estimators=600)]
model_dict = dict(zip(index,model_list))
model_dict


# In[20]:


pediction_outcome_list =[]
for i,j in model_dict.items():
    j.fit(x_train,y_train)
    x_prediction = j.predict(x_test)
    accuracy = accuracy_score(y_test, x_prediction)
    pediction_outcome_list.append(accuracy)
    print(i,"{:.4f}".format(accuracy))


# In[21]:


plt.figure(figsize = (10,4))
sn.barplot(x =index , y =pediction_outcome_list, palette="vlag",  ci=95,edgecolor='purple',n_boot=1000, dodge=False)


# In[22]:


gradient_boost = GradientBoostingClassifier(loss='deviance',  learning_rate=0.1)
result_list = []
accuracy = []
for j in range(1,28,1):
    x_train,x_test,y_train,y_test = train_test_split(x, y, test_size = 0.25, random_state = j)    
    gradient_boost_fit = gradient_boost.fit(x_train, y_train)
    fit_predict_x = gradient_boost_fit.predict(x_test)
    accuracy.append(accuracy_score(y_test, fit_predict_x))
    result_list.append(j)


# In[23]:


plt.figure(figsize=(10,8))
plt.xlabel("迭代次数",fontsize=14)
plt.
# In[ ]:

创作不易觉得有帮助请点赞关注收藏~~~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/62640.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！