参考
代码随想录
题目一:LeetCode 343.整数拆分
- 确定dp数组及其下标的含义
dp[i]为整数i拆分后得到的最大化乘积。 - 确定递推公式
dp[i]可以有两种方式得到:
dp[i] = j * (i-j),即只拆分成两个数,其中1 <= j <= i/2,最终dp[i]应该是所有j取值得到dp[i]中的最大值dp[i] = j * dp[i-j],这种情况相当于将整数i拆分成多个数,因为其中的dp[i-j]已经被拆分过了,至少被拆分成两个数,具体拆分成多少个数不用去管,其中1 <= j <= i/2,同样dp[i]也是所有取值中的最大值。
在具体的代码实现上,dp[i] = max(dp[i],j * (i - j),j * dp[i - j]),这样对于每个i,只需要遍历一遍j就可以得到dp[i]了。把dp[i]放到max函数中的目的就是不断更新最大值。
-
初始化dp数组
i = 0或1时,dp[i]是用不到的,所以不需要初始化只需要将dp[2]初始化为1,即dp[2] = 1。 -
确定遍历顺序
对于i,dp[i]需要由dp[i-j]来确定,所以i应该从小到大遍历;对于j,既可以从大到小也可以从小到大。 -
举例推导dp数组
以n = 10为例,根据下面的递推公式进行推导:
dp[i] = max(dp[i],j * (i - j),j * dp[i - j]),其中3 <= i <= 10,1 <= j <= i/2
推导得到的dp数组为[1,2,4,6,9,12,18,27,36](注意下标从2开始),因此dp[10] = 36。
具体的代码实现如下:
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n+1);
dp[2] = 1;
for(int i = 3; i <= n; i++)
for(int j = 1; j <= i/2; j++)
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));
return dp[n];
}
};
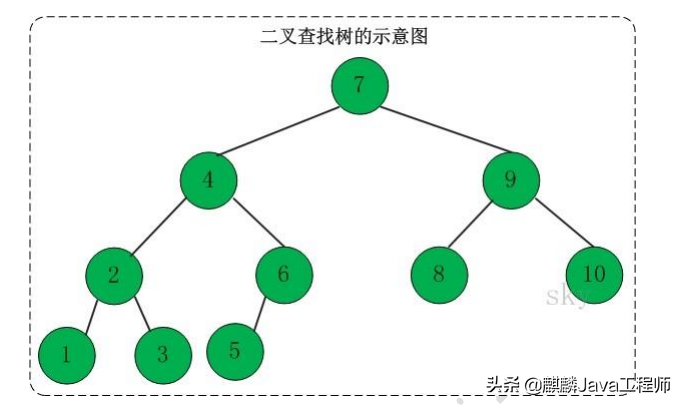
题目二:LeetCode 96.不同的二叉搜索树


感觉这个题更像是找规律的题目,但是这个规律很难看出来。
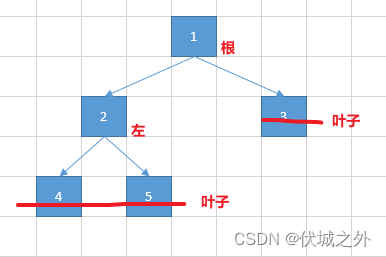
dp[3]就是元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
- 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。 - 确定递推公式
dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量 - dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。根据递推公式,dp[0] = 1. - 确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。那么遍历i里面每一个数作为头结点的状态,用j来遍历。 - 举例推导dp数组
当 n = 5时,dp数组为[1,1,2,5,14,42]
整体代码实现如下:
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};






![[附源码]计算机毕业设计JAVA疫苗接种管理系统](https://img-blog.csdnimg.cn/baf9ef2f7a804060ab4f6b887163a792.png)