目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

给定一个以顺序储存结构存储整数值的完全二叉树序列（最多1000个整数），请找出此完全二叉树的所有非叶子节点部分，然后采用后序遍历方式将此部分树（不包含叶子）输出。

1、只有一个节点的树，此节点认定为根节点（非叶子）。

2、此完全二叉树并非满二叉树，可能存在倒数第二层出现叶子或者无右叶子的情况

其他说明：二叉树的后序遍历是基于根来说的，遍历顺序为：左-右-根

输入描述

一个通过空格分割的整数序列字符串

输出描述

非叶子部分树结构。备注：输出数字以空格分隔

用例

输入	1 2 3 4 5 6 7
输出	2 3 1
说明	找到非叶子部分树结构，然后采用后序遍历输出。

题目解析

完全二叉树定义

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

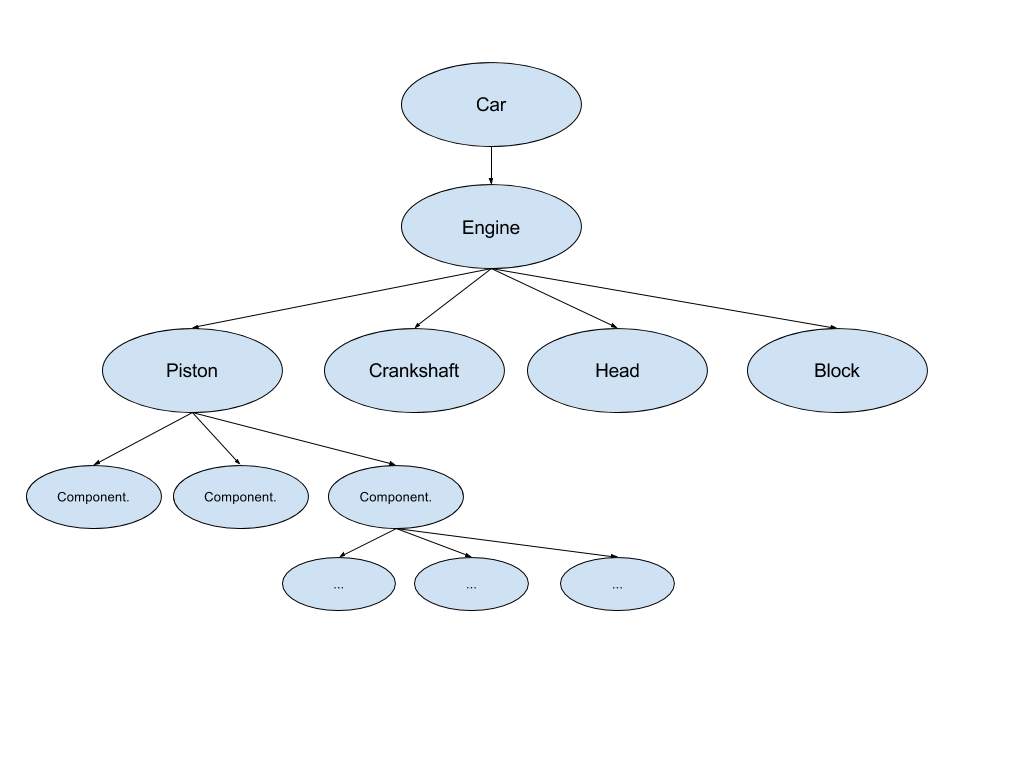
比如下图就是模拟向完全二叉树中加入元素，可以发现，新加入元素总是优先供给左子树，左子树满了，再考虑右子树。

 

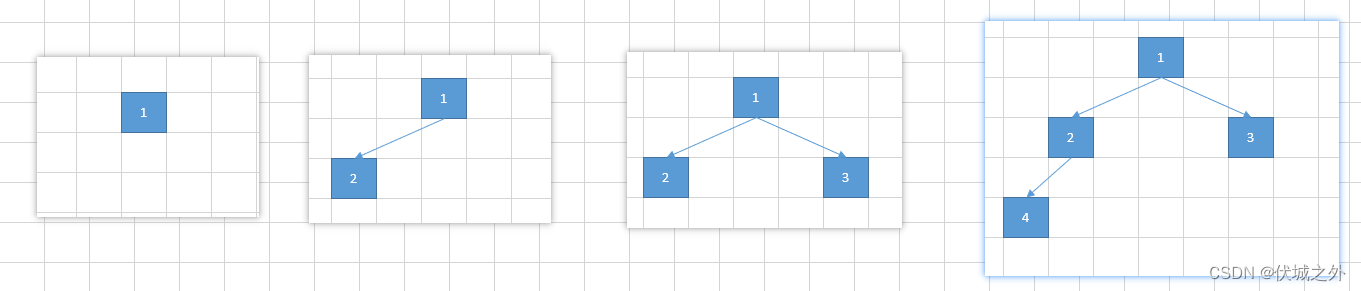
因为上面这个特性，完全二叉树可以用数组模拟，数组元素满足如下规律：

arr[i] 的左孩子是 arr[2*i+1] ，右孩子是 arr[2*i + 2]。（i从0开始计数）

比如数组 arr = [1,2,3,4]，则对应完全二叉树如下

 

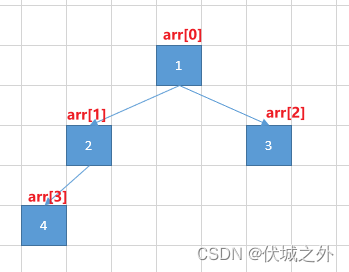
了解了完全二叉树和数组的关系后，本题的解决就非常简单了，不需要实现一个完全二叉树的数据结构，直接依赖于数组+深度递归就可以完成完全二叉树的后序遍历。

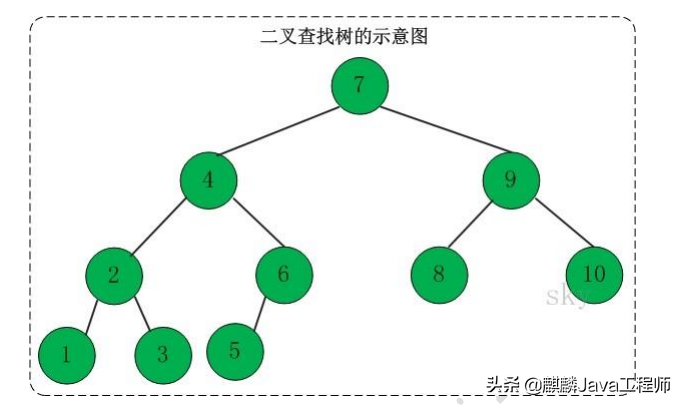
用例的示意图

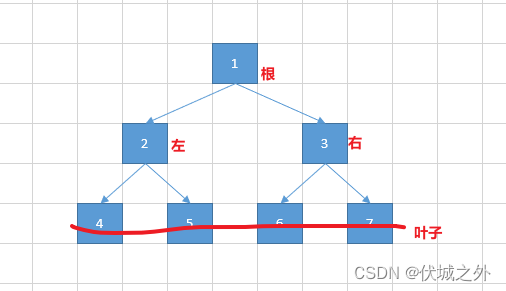
因此用例的后序遍历是：左-右-根，即2,3,1

由于题目要求不能遍历叶子节点，因此我们需要判定什么节点是叶子

 

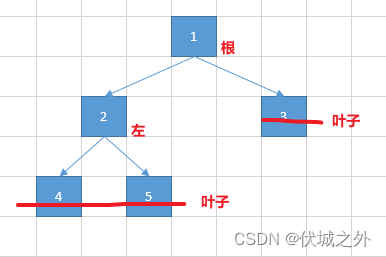
如上面两个图所示，只要该节点有左孩子，那么该节点就不是叶子，比如2节点。

因此我们只需要从数组第i个元素开始深度递归，递归逻辑：

假设第i个元素为根，那么它的左孩子是 arr[2*i+1]，右孩子是arr[2*i+2]：

1. 如果左孩子不为空，则说明第i个元素不是叶子，因此继续递归其左孩子，即将左孩子当成新的根来递归。如果递归到本身是叶子节点，则停止递归。
2. 如果右孩子也不为空，则根据后序遍历原则，还要对右孩子进行递归，即将右孩子也当成根。如果递归到本身是叶子节点，则停止递归。
3. 打印arr[i]

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

rl.on("line", (line) => {
  const arr = line.split(" ");
  console.log(getResult(arr));
});

function getResult(arr) {
  if (arr.length === 1) return arr[0];

  const res = [];
  dfs(arr, 0, res);

  return res.join(" ");
}

function dfs(arr, root, res) {
  let left = 2 * root + 1;
  let right = 2 * root + 2;

  if (arr[left]) {
    dfs(arr, left, res);
    if (arr[right]) dfs(arr, right, res);
    res.push(arr[root]);
  }
}